Решение системы уравнений является важным шагом в математике и существует необходимость в его доказательстве. Особенно это актуально, когда требуется найти единственное решение системы уравнений. Ведь уникальность решения может иметь большое значение в определенной области знаний или практическом применении.
Для доказательства единственности решения системы уравнений важно рассмотреть несколько факторов. Во-первых, необходимо убедиться, что каждое уравнение является реальным и верным. Это можно сделать, подставив найденные значения переменных в каждое уравнение системы и убедившись, что обе его части равны. При этом следует учитывать, что система уравнений может быть как линейной, так и нелинейной, что накладывает свои ограничения на выбор методов доказательства.
Во-вторых, для доказательства единственности решения системы уравнений важно рассмотреть количество уравнений и переменных в системе. Если число уравнений равно числу переменных, то система имеет единственное решение. Это следует из теоремы Кронекера-Капелли, которая утверждает, что система уравнений с квадратной матрицей коэффициентов имеет единственное решение, если определитель этой матрицы отличен от нуля.
Исследование системы уравнений на единственность решения может потребовать применения различных методов, таких как метод Гаусса или обратной матрицы. Важно помнить, что доказательство единственности решения системы уравнений требует тщательного анализа и выявления всех возможных вариантов.
Существует только одно решение системы уравнений: как это проверить?
Предположим, у нас есть система уравнений, и мы хотим узнать, существует ли у нее только одно решение. Существует несколько способов проверить это.
- Метод Гаусса
- Матричный метод
- Сравнение числа уравнений и переменных
- Проверка наличия решения
Одним из самых распространенных методов является метод Гаусса. С помощью этого метода можно привести систему к ступенчатому виду и выяснить количество свободных переменных. Если после приведения системы к ступенчатому виду нет свободных переменных, то решение единственное.
Другой способ - использовать матричный метод. Для этого нужно составить матрицу коэффициентов системы уравнений и определитель этой матрицы. Если определитель матрицы не равен нулю, то система имеет только одно решение.
Также можно проверить количество уравнений и переменных в системе. Если количество уравнений равно количеству переменных, и все уравнения независимы, то решение системы будет единственным.
Если мы уже знаем, что система имеет хотя бы одно решение, то мы можем решить систему численно и проверить, существует ли только одно решение. Если при решении получаем одно конкретное значение для каждой переменной, то решение единственное.
Важно понимать, что данные методы не всегда дают 100% уверенность в том, что система имеет только одно решение. Иногда для полной уверенности требуется применение нескольких методов проверки.
Разбор возможных вариантов решений системы уравнений

Для доказательства существования единственного решения системы уравнений необходимо разобрать все возможные варианты и исключить все остальные возможности.
1. Вариант единственного решения: в системе присутствуют столько же уравнений, сколько и неизвестных переменных, при этом ранг матрицы системы равен количеству неизвестных. В этом случае существует единственное решение, которое можно найти при помощи метода Крамера или метода Гаусса.
2. Вариант бесконечного числа решений: если ранг матрицы системы меньше количества неизвестных переменных, то система имеет бесконечное количество решений. В этом случае можно использовать метод Гаусса для нахождения базисного решения, а затем описать общее решение с помощью параметров.
3. Вариант отсутствия решений: если ранг матрицы системы меньше количества неизвестных переменных и в системе присутствует противоречие, то система не имеет решений. В этом случае следует привести систему к противоречию, например, путем умножения уравнения на ненулевое число или сложения уравнений с противоположными знаками.
Таким образом, для доказательства существования единственного решения системы уравнений необходимо провести анализ всех возможных вариантов и исключить все остальные возможности.
Установление условий существования единственного решения

Для того чтобы система уравнений имела единственное решение, необходимо и достаточно выполнение определенных условий. Рассмотрим эти условия подробнее.
1. Число уравнений должно быть равно числу неизвестных. Если число уравнений больше числа неизвестных, то система будет иметь либо бесконечное количество решений, либо не иметь решений вовсе. Если число уравнений меньше числа неизвестных, то система также не имеет решений вовсе.
2. Матрица коэффициентов системы должна быть невырожденной. Это означает, что определитель матрицы должен быть отличен от нуля. Если определитель равен нулю, то система имеет либо бесконечное количество решений, либо не имеет решений вовсе.
3. Уравнения системы должны быть независимыми. Это означает, что ни одно уравнение не может быть выражено через другие уравнения системы. Если одно или несколько уравнений являются линейно зависимыми, то система будет иметь бесконечное количество решений.
Для определения условий существования единственного решения системы уравнений удобно использовать метод Гаусса или метод Крамера. Эти методы позволяют привести систему к эквивалентной системе, у которой сразу видно, выполняются ли указанные условия.
| Условие | Результат |
| Число уравнений = число неизвестных | Единственное решение |
| Определитель матрицы ≠ 0 | Единственное решение |
| Линейно независимые уравнения | Единственное решение |
Если все указанные условия выполняются, то система уравнений имеет единственное решение. В противном случае, система может иметь бесконечное количество решений или не иметь решений вовсе. Поэтому необходимо тщательно анализировать условия для установления существования единственного решения системы уравнений.
Процесс доказательства уникальности решения
1. Анализ системы уравнений: В первую очередь необходимо тщательно проанализировать систему уравнений. Изучите все уравнения, коэффициенты и условия системы. Найдите как можно больше информации о системе уравнений, такую как количество уравнений и переменных, их тип, зависимость и т. д.
2. Использование математических методов: Как только вы изучите систему уравнений, вам потребуется использовать математические методы для доказательства уникальности решения. Это может включать методы вычислений, разложения, преобразований и т. д. Выберите методы, которые наилучшим образом соответствуют вашей системе уравнений и помогут вам доказать уникальность решения.
3. Применение логики и рассуждения: В процессе доказательства уникальности решения вы также будете использовать логику и рассуждения. Вам нужно будет обосновать каждый шаг, используя логическое мышление и приводя аргументы, которые доказывают правильность и закономерность ваших действий.
4. Проверка решения: После завершения доказательства уникальности решения, вам следует проверить его. Подставьте найденное решение в систему уравнений и убедитесь, что оно удовлетворяет каждому уравнению. Если решение соответствует уравнениям, то вы успешно доказали уникальность его существования в данной системе.
Применение метода разложения на множители

Для решения системы уравнений с использованием метода разложения на множители следуют следующие шаги:
- Разложите каждое уравнение на множители.
- Приравняйте каждый множитель к нулю и решите полученные уравнения.
- Проверьте найденные значения, подставив их в исходные уравнения системы.
Если при подстановке полученных значений в исходные уравнения все они верны, то найденные значения являются решениями системы уравнений.
Применение метода разложения на множители позволяет найти точное решение системы уравнений, если таковое существует. Он особенно полезен при решении квадратных уравнений или систем уравнений с квадратными членами.
Анализ значений ограничений и оговорок
Для доказательства существования единственного решения системы уравнений необходимо провести анализ значений ограничений и оговорок. Этот анализ позволит определить, выполняются ли все условия, которые позволяют системе уравнений иметь только одно решение.
В первую очередь нужно убедиться, что система уравнений не содержит противоречий. Противоречие может проявляться, когда одно из уравнений противоречит другому или когда решения одного из уравнений противоречат решениям других уравнений. Если будет обнаружено противоречие, то система уравнений не имеет решений или имеет бесконечное множество решений, в зависимости от характера противоречия.
Далее следует проверить выполнение оговорок системы уравнений. Оговорки могут представляться в виде условий, которые должны выполняться для решения системы. Например, уравнения могут иметь ограничения на диапазон значений переменных или на соотношения между переменными. Если оговорки не выполняются, то система уравнений может иметь некоторые или все решения из условий оговорок.
Наконец, необходимо провести анализ значений ограничений, которые не являются оговорками системы уравнений. Такие ограничения могут свидетельствовать о наличии единственного решения системы. Например, если система уравнений содержит уравнение с неравенством и оно имеет решение, то это указывает на существование единственного решения системы, которое удовлетворяет этому неравенству.
Таким образом, проведение анализа значений ограничений и оговорок позволяет определить, существует ли единственное решение системы уравнений. В случае соблюдения всех условий система будет иметь только одно решение, и нахождение этого решения будет возможно.
Демонстрация единственности решения через матричное представление
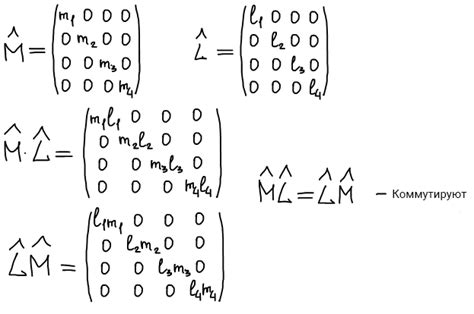
Единственность решения системы уравнений можно доказать, используя матричное представление системы. В матричной форме уравнения системы записываются в виде произведения матрицы коэффициентов на вектор неизвестных:
Ax = b
Где A - матрица коэффициентов системы, x - вектор неизвестных и b - вектор свободных членов.
Если матрица коэффициентов A имеет полный ранг, то она обратима, а следовательно, уравнение имеет единственное решение. Иначе говоря, система уравнений имеет единственное решение только в том случае, когда определитель матрицы коэффициентов не равен нулю.
Чтобы доказать, что решение системы уравнений единственно, можно проверить, является ли матрица коэффициентов обратимой. Для этого можно вычислить определитель матрицы и убедиться, что он не равен нулю:
det(A) ≠ 0
Если определитель не равен нулю, то система уравнений имеет единственное решение, которое можно найти путем обратного преобразования матрицы:
x = A⁻¹b
Где A⁻¹ - обратная матрица коэффициентов, а x - вектор решений.
Таким образом, демонстрация единственности решения системы уравнений через матричное представление позволяет убедиться в том, что решение системы существует и является единственным при выполнении условия ненулевого определителя матрицы коэффициентов.
Решение системы уравнений с помощью линейного анализа

Когда мы сталкиваемся с системой уравнений, наша задача состоит в том, чтобы найти значения, удовлетворяющие всем уравнениям системы. Возникает вопрос: существует ли только одно такое решение, и если да, как его доказать?
Для начала необходимо выполнить линейный анализ системы уравнений. Это подразумевает приведение системы к матричному виду и применение методов линейной алгебры для нахождения ее решений. Основной инструмент, которым мы пользуемся, это матричные операции и методы приведения матрицы к улучшенному ступенчатому виду.
Важно отметить, что линейный анализ может также показать, что система не имеет решений или имеет бесконечное количество решений. Однако, когда мы доказываем существование единственного решения системы, основная идея заключается в получении улучшенного ступенчатого вида матрицы системы.
Рассмотрение графического метода доказательства единственности решения
Для начала, необходимо построить графики всех уравнений системы на плоскости. При этом каждое уравнение представляется в виде прямой линии или кривой, в зависимости от его типа.
Затем, необходимо исследовать поведение графиков и определить точки пересечения. Если система имеет единственное решение, то графики уравнений пересекаются в одной точке. Это означает, что только одна пара значений переменных удовлетворяет обоим уравнениям системы.
Если же графики уравнений параллельны или не пересекаются вовсе, то система не имеет решений или имеет бесконечно много решений.
Графический метод позволяет наглядно исследовать, какие условия должны быть выполнены, чтобы система имела единственное решение. В результате, можно получить уверенность в правильности решения системы уравнений и доказать его единственность.
Использование алгоритмов решения для проверки уникальности

Один из таких алгоритмов - метод Гаусса-Жордана. С его помощью система уравнений приводится к ступенчатой форме, после чего можно определить количество свободных переменных. Если число свободных переменных равно нулю, то система имеет единственное решение. Если же число свободных переменных больше нуля, то существует бесконечное число решений.
Алгоритмы решения систем уравнений, такие как метод Гаусса-Жордана, позволяют не только определить уникальность решений, но и найти сами решения системы. После приведения системы уравнений к ступенчатой форме, можно использовать обратную подстановку, чтобы найти значения неизвестных. Если система имеет единственное решение, то это будет точное значение для всех переменных.
Для проверки уникальности решений системы уравнений можно также использовать метод Крамера. Он основан на вычислении определителей матриц и позволяет определить, существует ли единственное решение системы. Если определитель матрицы системы равен нулю, то система имеет бесконечное число решений или не имеет их вовсе. В противном случае, система имеет единственное решение.
Таким образом, использование алгоритмов решения систем уравнений позволяет проверить уникальность и найти значения неизвестных в системе. Такие алгоритмы являются неотъемлемой частью математического и инженерного анализа и позволяют решать разнообразные задачи с высокой степенью точности и эффективности.
| Пример системы уравнений | Решение |
|---|---|
| 2x + y = 5 | x = 2, y = 1 |
| 3x - 2y = 4 |



