Параллелограмм – это четырехугольник, у которого противоположные стороны параллельны и равны. Существует несколько интересных свойств параллелограмма, одно из которых связано с равенством его диагоналей.
Условием существования равных диагоналей в параллелограмме является его особое строение. Углы при вершинах параллелограмма должны быть равными, то есть противоположные вершины должны быть равными. Кроме того, стороны параллелограмма должны быть параллельны и равными друг другу.
Доказательство равенства диагоналей параллелограмма можно провести, используя свойства параллелограмма и прямых линий. Если взглянуть на параллелограмм, то можно увидеть, что он содержит два треугольника, которые имеют по двум равным сторонам (стороны параллелограмма). Следовательно, эти два треугольника равны по третьей стороне, которой является диагональ параллелограмма. Таким образом, длины диагоналей параллелограмма равны между собой.
Равенство диагоналей в параллелограмме часто используется при решении геометрических задач. Зная данное свойство, можно легко найти длины диагоналей или использовать их для нахождения других значений в параллелограмме.
Условие параллелограмма
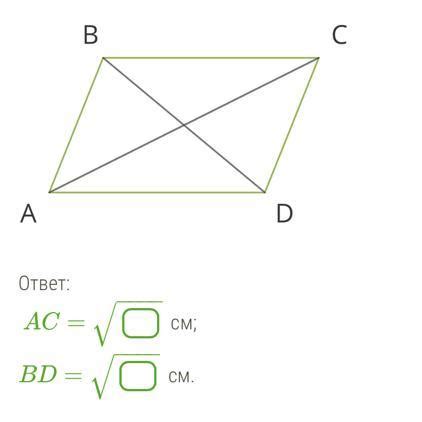
Формально, параллелограмм можно определить следующими условиями:
- Противоположные стороны параллельны: AB



