Трапеция – это четырехугольник, который имеет две параллельные стороны. Трапеция называется равнобокой, если дополнительные основания равны, то есть параллельные стороны одинаковой длины. Одно из самых интересных и необычных свойств равнобокой трапеции заключается в том, что она может быть вписана в окружность.
Мы предлагаем вам в этой статье узнать, как доказать, что трапеция вписанная в окружность равнобокая. В качестве примеров мы рассмотрим несколько доказательств, которые помогут вам лучше понять это удивительное свойство трапеции.
Первое доказательство является геометрическим. Мы посмотрим на углы, стороны и диаметры для определенных треугольников, которые образуются в равнобокой трапеции. Затем мы воспользуемся свойствами окружностей и углами, чтобы получить равенство, доказывающее, что трапеция вписанная в окружность равнобокая.
Трапеция вписанная в окружность: определение и особенности
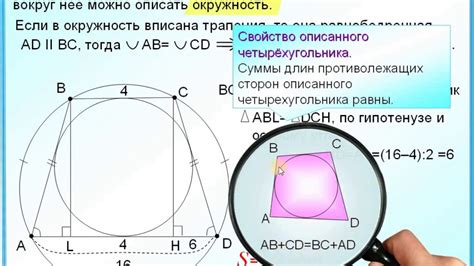
Основной особенностью вписанной трапеции является то, что она удовлетворяет следующему свойству: сумма углов при основаниях трапеции равна 180 градусов. Это свойство легко объясняется тем, что основания трапеции являются хордами окружности, а углы, образованные хордами и дугами, равны половине центрального угла, соответствующего этой дуге. Таким образом, сумма углов при основаниях равна сумме центральных углов, то есть 180 градусов.
Величина угла между непараллельными сторонами вписанной трапеции равна половине разности центральных углов, соответствующих этим сторонам. Также, трапеция вписанная в окружность имеет два дополнительных свойства: диагонали трапеции являются радиусами окружности, а сумма противоположных углов трапеции также равна 180 градусов.
Трапеция вписанная в окружность является одним из важных объектов в геометрии, и ее свойства имеют широкое применение в различных задачах и теоремах.
Понятие вписанной трапеции в геометрии:
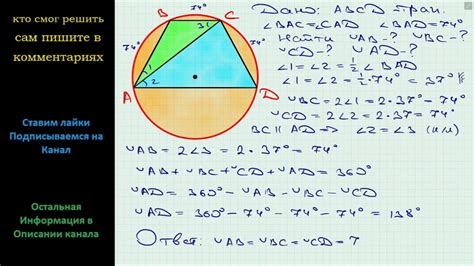
У вписанной трапеции есть несколько интересных свойств. Одно из них заключается в том, что сумма противоположных углов трапеции всегда равна 180 градусов. Также стороны вписанной трапеции обладают особенным соотношением: сумма длин оснований трапеции равна произведению длин ее диагоналей. Это свойство можно использовать при доказательстве равнобокости вписанной трапеции.
Основные признаки равнобокой трапеции:
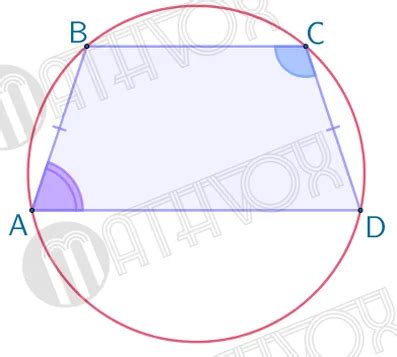
Такая трапеция обладает следующими свойствами:
- Боковые стороны параллельны между собой.
- Углы, образованные боковыми сторонами и равными основаниями, равны между собой.
- Сумма углов, образованных боковыми сторонами, равна 180 градусам.
- Основания и диагональ, соединяющая вершины боковых сторон, образуют равнобедренный треугольник.
- Перпендикуляр, опущенный из середины основания на боковую сторону, делит ее пополам.
- Биссектрисы углов, образованных боковыми сторонами и равными основаниями, пересекаются в точке на диагонали, деля ее пополам.
Таким образом, равенство длин оснований и боковых сторон, а также равенство углов делает равнобокую трапецию симметричной и уникальной фигурой с большим количеством интересных свойств.
Свойства равнобоких трапеций:
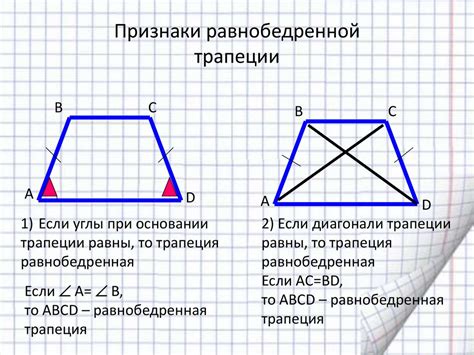
1. Углы оснований
У равнобокой трапеции углы при основаниях равны. Это означает, что если один из углов оснований равен 90 градусов, например, то второй угол оснований также будет равен 90 градусов.
2. Диагонали
Диагонали равнобокой трапеции равны величиной и перпендикулярны друг другу. То есть, если AC и BD – диагонали равнобокой трапеции ABCD, то AC = BD и AC ⊥ BD.
3. Углы между диагоналями
Угол между диагоналями равнобокой трапеции равен 180 минус сумма углов между основаниями. То есть, если ∠A и ∠B – углы между диагоналями AC и BD, а ∠C и ∠D – углы при основаниях AB и CD соответственно, то ∠A + ∠B = 180 – (∠C + ∠D).
Эти свойства делают равнобокие трапеции интересными объектами для исследования и использования в геометрии.
Доказательство равнобокости вписанной трапеции:

Пусть ABCD - вписанная трапеция, где AB и CD - пары параллельных сторон.
Так как ABCD - вписанная фигура, то сумма углов ADC и ABC будет равна 180 градусам.
Также, так как AB



