Треугольник - одна из основных геометрических фигур, изучение которой позволяет понять и применить множество математических законов и теорем. Одной из важных характеристик треугольника является отношение стороны к синусу угла, которое имеет большое значение в тригонометрии и геометрии в целом.
Отношение стороны к синусу треугольника выражается формулой a/sin(A) = b/sin(B) = c/sin(C), где a, b и c - стороны треугольника, а A, B и C - соответствующие им углы. Это равенство, известное как закон синусов, позволяет определить отношение между сторонами и углами треугольника даже без знания их точных значений.
Математическое доказательство закона синусов основано на использовании геометрических свойств треугольников и определении синуса угла. Однако, для более наглядного понимания и демонстрации данного закона, полезно рассмотреть несколько примеров.
Пример 1:
Предположим, у нас есть треугольник со сторонами a = 6, b = 8 и углом A = 30 градусов. Определим отношение стороны c к синусу угла C, используя формулу отношения стороны к синусу: c/sin(C) = a/sin(A).
В данном случае, зная сторону и угол треугольника, мы можем заменить соответствующие значения в формулу: c/sin(C) = 6/sin(30). Находим синус 30 градусов, который равен 0.5, и заменяем его в формуле: c/0.5 = 6/0.5.
Упрощаем формулу и находим значение стороны c: c = 6/0.5, c = 12. Таким образом, сторона c треугольника равна 12.
Пример 2:
Рассмотрим треугольник со сторонами a = 10, b = 12 и углом B = 45 градусов. Используя формулу отношения стороны к синусу, мы можем определить значение стороны c: c/sin(C) = b/sin(B).
Подставляем известные значения в формулу: c/sin(C) = 12/sin(45). Синус 45 градусов равен 0.707, поэтому заменяем его в уравнении: c/0.707 = 12/0.707.
Производим упрощение и находим значение стороны c: c = 12/0.707, c ≈ 16.97. Таким образом, сторона c треугольника примерно равна 16.97.
Как видно из этих примеров, отношение стороны треугольника к синусу угла позволяет определить значение неизвестной стороны треугольника, используя известные стороны и углы. Это важное математическое доказательство, которое широко применяется в различных областях знаний и позволяет решать задачи связанные с треугольниками и тригонометрией.
Отношение стороны треугольника к синусу: математическое доказательство и примеры
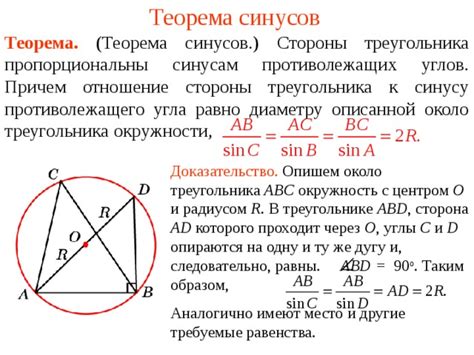
Математическое доказательство данного отношения основано на определении синуса угла через противоположную сторону треугольника и длину гипотенузы в прямоугольном треугольнике.
Пусть дан треугольник ABC, где угол A равен α. Пусть a - сторона, противолежащая углу α. Тогда справедливо следующее равенство:
a/sin(α) = b/sin(β) = c/sin(γ)
где b и c - прочие стороны треугольника, β и γ - соответствующие углы.
Таким образом, данное равенство говорит о том, что отношение длины каждой стороны треугольника к синусу соответствующего угла остается неизменным.
Для наглядности, рассмотрим пример:
Дан прямоугольный треугольник ABC, где угол A равен 30°, b = 4 и c = 6.
Используя отношение стороны треугольника к синусу, мы можем найти длину стороны a:
a/sin(30°) = 6/sin(90°)
a = 6 * sin(30°) = 6 * 1/2 = 3
Таким образом, длина стороны a равна 3.
Отношение стороны треугольника к синусу является важным инструментом в решении задач, связанных с треугольниками и тригонометрией. С его помощью мы можем находить неизвестные стороны треугольника, зная длины других сторон и соответствующие углы.
Математическое определение синуса
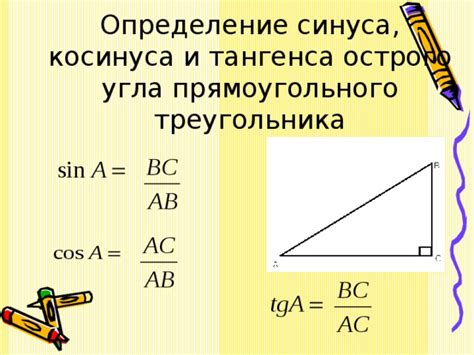
Математический синус угла α (обозначается sin(α)) определяется как отношение противолежащего катета к гипотенузе в прямоугольном треугольнике.
Формула для вычисления синуса:
- sin(α) = противолежащий катет / гипотенуза
Значение синуса α лежит в диапазоне от -1 до 1. Синус прямого угла равен 1, а при угле 90 градусов.
Синус является периодической функцией с периодом 2П, где П - это число «пи», приближенно равное 3.1416.
Связь между стороной треугольника и синусом угла
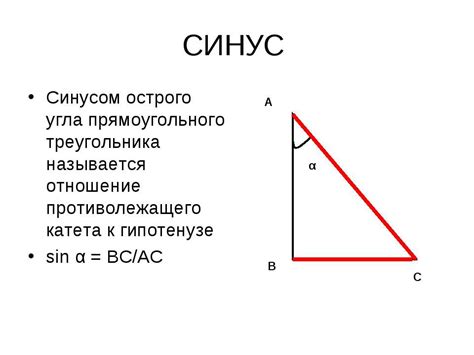
В геометрии существует тесная связь между стороной треугольника и синусом угла. Это важное свойство можно проиллюстрировать математическим доказательством и примерами.
Математическое доказательство основано на применении тригонометрической функции синуса. В треугольнике ABC, где угол A равен α, сторона a соответствует этому углу, то есть a = BC. Применяя теорему синусов, можно установить следующую связь:
Синус угла α = (Сторона a) / (Гипотенуза)
Данная формула позволяет определить синус угла α, если известна сторона a и гипотенуза треугольника. Также можно использовать обратную формулу для определения стороны треугольника по значениям синуса угла и гипотенузы.
Примеры:
Пример 1: Рассмотрим прямоугольный треугольник со сторонами a = 3 и гипотенузой c = 5. Найдем значение синуса угла α.
Используя формулу, получаем: sin α = 3/5 ≈ 0.6.
Пример 2: Рассмотрим треугольник со сторонами a = 4, b = 7 и углом α = 60°. Найдем значение стороны c с помощью синуса этого угла.
Применяя обратную формулу, получим: c = b / sin α = 7 / sin 60° ≈ 8.08.
Синус угла является важным инструментом для решения геометрических задач и нахождения неизвестных значений сторон треугольников. Понимание связи между стороной треугольника и синусом угла позволяет решать различные задачи, связанные с треугольниками и тригонометрией.
Измерение углов треугольника и отношение к синусу
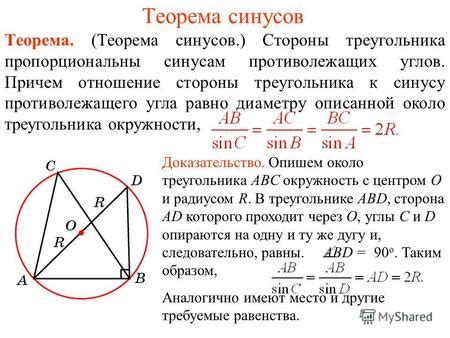
Для изучения свойств треугольников и вычисления их сторон и углов, необходимо знать, как измерять углы треугольника. Углы могут быть измерены в градусах, радианах или градах.
Отношение сторон треугольника к синусу является одним из фундаментальных математических соотношений. Оно позволяет нам вычислять сторону треугольника, зная длину другой стороны и величину одного из углов. Формула такого отношения выглядит следующим образом:
| Сторона треугольника | Отношение к синусу угла |
|---|---|
| a | a/sin(A) |
| b | b/sin(B) |
| c | c/sin(C) |
Где a, b и c - длины сторон треугольника, а A, B и C - величины углов треугольника (измеряемые в радианах или градусах).
Пример:
Допустим, у нас есть треугольник ABC, где сторона AB равна 5 единицам, угол A составляет 45 градусов. Мы хотим найти длину стороны AC треугольника.
Используя формулу отношения стороны к синусу, мы можем записать:
AC = AB/sin(A)
AC = 5/sin(45°)
Угол 45 градусов мы можем выразить в радианах: 45° * π/180° = π/4 радиан.
AC = 5/sin(π/4)
С помощью калькулятора или таблицы значений тригонометрических функций, мы можем вычислить значение синуса угла π/4, которое равно √2/2.
AC = 5/(√2/2)
Упростим выражение, умножив обе части на 2:
AC = 5 * 2/√2 ≈ 7.07
Таким образом, длина стороны AC треугольника равна примерно 7.07 единицам.
Математическое доказательство формулы отношения стороны треугольника к синусу
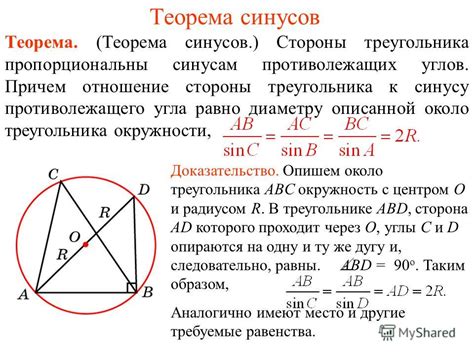
Чтобы доказать формулу отношения стороны треугольника к синусу, начнем с рассмотрения общего треугольника ABC. Пусть стороны треугольника обозначаются как a, b и c, а противолежащие углы обозначаются как A, B и C соответственно.
Используя теорему синусов, мы можем установить следующие соотношения:
- sin A / a = sin B / b = sin C / c
- sin A = (a * sin B) / b
- a * sin B = b * sin A
Теперь докажем, что отношение стороны треугольника к синусу справедливо для стороны a:
- Предположим, что сторона a соответствует углу A.
- Мы знаем, что sin A = a / c, согласно определению синуса прямоугольного треугольника.
- Заменив sin A в уравнении a * sin B = b * sin A на a / c, мы получаем: a * sin B = b * (a / c).
- После сокращения на a получаем: sin B = b / c.
- Таким образом, мы показали, что отношение стороны b к синусу угла B (sin B) равно отношению стороны a к стороне c (b / c).
Аналогично можно доказать, что отношение стороны c к синусу угла C также равно отношению стороны a к стороне c, то есть c / sin C = a / sin A.
Таким образом, мы получаем формулу отношения стороны треугольника к синусу:
a / sin A = b / sin B = c / sin C
Примеры использования формулы отношения стороны треугольника к синусу
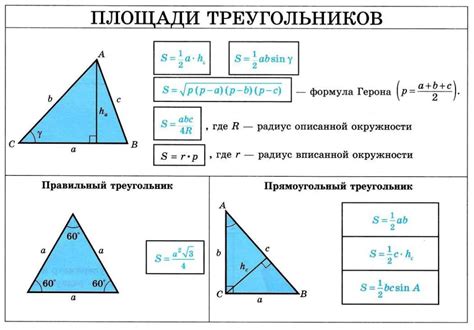
Ниже приведены несколько примеров использования этой формулы:
Пример 1:
Рассмотрим прямоугольный треугольник, в котором один из углов равен 30 градусам. Пусть длина гипотенузы равна 10 единицам. Чтобы найти длину противоположной стороны, используем формулу:
сторона = гипотенуза * синус(угол)сторона = 10 * sin(30)сторона ≈ 5Таким образом, длина противоположной стороны равна около 5 единиц.
Пример 2:
Рассмотрим равносторонний треугольник, в котором все углы равны 60 градусам. Пусть длина одной стороны равна 8 единицам. Чтобы найти длину противоположной стороны, используем формулу:
сторона = сторона * синус(угол)сторона = 8 * sin(60)сторона ≈ 6.928Таким образом, длина противоположной стороны равна около 6.928 единицы.
Пример 3:
Рассмотрим произвольный треугольник ABC. Пусть сторона AB равна 5 единицам, угол B равен 45 градусам. Чтобы найти длину противоположной стороны BC, используем формулу:
сторона = сторона * синус(угол)сторона = 5 * sin(45)сторона ≈ 3.535Таким образом, длина противоположной стороны BC равна около 3.535 единицы.
Как видно из примеров, формула отношения стороны треугольника к синусу позволяет находить длину противоположной стороны с помощью геометрических и тригонометрических вычислений.
Закономерности в отношении стороны треугольника к синусу
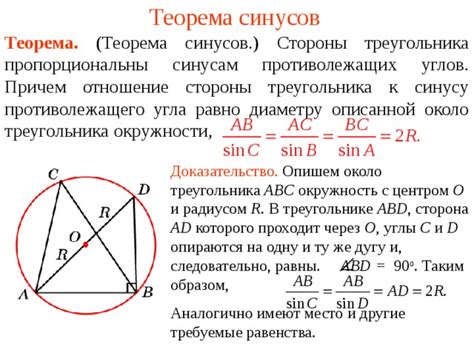
Закон синусов устанавливает, что отношение каждой стороны треугольника к синусу противолежащего ей угла равно константе. Формула закона синусов выглядит следующим образом:
a/sin(A) = b/sin(B) = c/sin(C),
где a, b и c - длины сторон треугольника, A, B и C - соответствующие им углы, а sin(A), sin(B) и sin(C) - их синусы.
Закон косинусов предоставляет другую закономерность в отношении стороны треугольника к синусу. Он устанавливает, что квадрат длины стороны треугольника равен сумме квадратов длин остальных двух сторон, умноженных на косинус противолежащего угла. В математической форме закон косинусов записывается так:
a^2 = b^2 + c^2 - 2bc * cos(A),
где a, b и c - длины сторон треугольника, A - противолежащий угол, cos(A) - его косинус.
Закономерности в отношении стороны треугольника к синусу являются важными инструментами в геометрии, которые позволяют решать различные задачи, связанные с треугольниками. На основе этих закономерностей можно определить длины сторон и углы, а также проводить различные вычисления и измерения треугольников.
Практическое применение отношения стороны треугольника к синусу
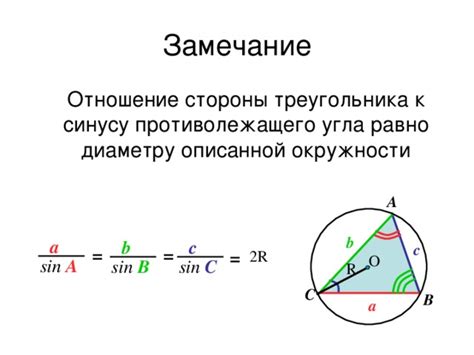
Одной из наиболее распространенных применений отношения стороны треугольника к синусу является решение задач, которые требуют вычисления неизвестных сторон или углов треугольника. Например, с помощью этого отношения можно определить длину недостающей стороны треугольника, зная длины двух других сторон и угол между ними. Это может быть полезно при проектировании строений или решении задач, связанных с планированием маршрутов на карте.
Также, отношение стороны треугольника к синусу может использоваться для определения углов треугольника по известным сторонам. Например, в навигации, с помощью этого отношения можно определить углы направления движения судна или самолета относительно известных точек на карте. Это позволяет пилоту или капитану судна точно определить свое положение и направление.
Еще одним практическим применением отношения стороны треугольника к синусу является вычисление высоты объектов. Например, используя длину известной стороны треугольника и измерения угла между этой стороной и горизонтальной плоскостью, можно вычислить высоту дерева или здания с помощью теодолита или других инструментов.




