Математика - это увлекательная и точная наука, которая изучает числа, формулы, графики и многое другое. В учебнике Мерзляка для 8 класса рассматривается тема о равенстве множеств, которая является важным понятием в алгебре.
Определение равенства множеств заключается в том, что два множества считаются равными, если они содержат одни и те же элементы. Для доказательства равенства множеств необходимо и достаточно доказать, что каждый элемент одного множества принадлежит другому множеству, и наоборот. Это можно сделать с помощью математических операций.
В учебнике Мерзляка для 8 класса представлены различные примеры доказательства равенства множеств. Одним из наиболее распространенных методов является доказательство по включению. Суть этого метода заключается в том, что если множество A включено в множество B, и множество B включено в множество A, то множества A и B равны. Данный метод является простым и понятным для учащихся.
В учебнике также приводятся и другие методы доказательства равенства множеств, например, доказательство по определению или по свойствам операций над множествами. Каждый из этих методов имеет свои особенности и подходит для разных задач.
Раздел 1: Определение равенства множеств

Математическим обозначением равенства множеств является знак "=": A = B.
Докажем равенство двух множеств А и В. Для этого необходимо показать, что каждый элемент множества А принадлежит множеству В, и наоборот. Формально это может быть записано следующим образом:
1) Для каждого элемента x из А, x ∈ В
2) Для каждого элемента y из В, y ∈ А
Пример:
Даны два множества А и В:
A = {1, 2, 3, 4}
B = {2, 3, 4, 1}
Чтобы доказать равенство множеств А и В, необходимо показать, что каждый элемент одного множества принадлежит другому множеству:
Для множества А:
1) 1 ∈ B
2) 2 ∈ B
3) 3 ∈ B
4) 4 ∈ B
Для множества В:
1) 2 ∈ A
2) 3 ∈ A
3) 4 ∈ A
4) 1 ∈ A
Таким образом, все элементы множества А принадлежат множеству В и наоборот, поэтому множества А и В равны: A = B.
Раздел 2: Математические операции над множествами
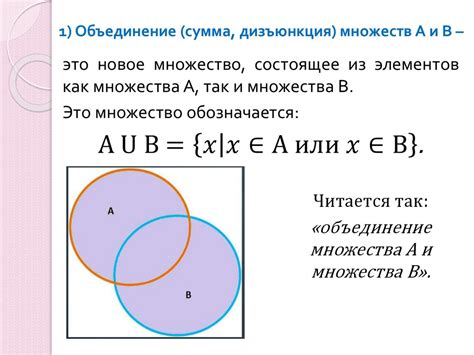
Операции над множествами включают в себя следующие:
- Объединение множеств: данная операция позволяет объединить два множества в одно, включая все их элементы. Обозначается символом ∪. Например, если у нас есть множество A = {1, 2, 3} и множество B = {2, 3, 4}, то их объединение будет A ∪ B = {1, 2, 3, 4}.
- Пересечение множеств: данная операция позволяет найти общие элементы двух множеств. Обозначается символом ∩. Например, если у нас есть множество A = {1, 2, 3} и множество B = {2, 3, 4}, то их пересечение будет A ∩ B = {2, 3}.
- Разность множеств: данная операция позволяет найти элементы, которые входят в одно множество, но не входят в другое. Обозначается символом \ или -. Например, если у нас есть множество A = {1, 2, 3} и множество B = {2, 3, 4}, то их разность будет A \ B = {1} и B \ A = {4}.
- Дополнение множества: данная операция позволяет найти все элементы, которые не входят в заданное множество. Обозначается символом '. Например, если у нас есть универсальное множество U = {1, 2, 3, 4, 5}, а множество A = {2, 3}, то дополнение множества A будет A' = {1, 4, 5}.
Понимание и умение использовать эти операции позволяет нам решать задачи, связанные с множествами, с легкостью и точностью. Запомните эти операции и приведенные примеры, чтобы успешно выполнять задания из учебника Мерзляка для 8 класса и других математических задач.
Раздел 3: Объединение множеств

В математике существует операция, называемая объединением множеств. Объединение двух множеств A и B представляет собой множество, содержащее все элементы из A и B без повторений. Операция объединения обозначается символом ∪.
Для двух множеств A = {a, b, c} и B = {c, d, e}, объединение будет выглядеть следующим образом:
- A ∪ B = {a, b, c, d, e}
То есть, в результате объединения множеств A и B мы получаем новое множество, в которое входят все элементы из обоих исходных множеств без дублирования.
Операция объединения множеств имеет несколько свойств:
- Коммутативность: A ∪ B = B ∪ A
- Ассоциативность: (A ∪ B) ∪ C = A ∪ (B ∪ C)
- Существование нейтрального элемента: A ∪ ∅ = A
Объединение множеств широко применяется в различных областях математики, а также в программировании и информатике. Эта операция позволяет объединять и анализировать данные из различных источников, а также решать множество задач, связанных с объединением и нахождением общих элементов.
Раздел 4: Пересечение множеств

В этом разделе мы рассмотрим операцию пересечения множеств, которая позволяет найти общие элементы двух или более множеств. Пересечение обозначается символом ∩ (знаком пересечения).
Для нахождения пересечения множеств необходимо взять все элементы, которые есть одновременно во всех заданных множествах. Если элемент присутствует только в одном или нескольких множествах, но отсутствует в остальных, то он не будет входить в пересечение.
Для наглядности, рассмотрим следующий пример:
Пусть заданы два множества: A = {1, 2, 3, 4, 5} и B = {4, 5, 6, 7}. Чтобы найти их пересечение, мы просто указываем элементы, которые есть в обоих множествах: A ∩ B = {4, 5}.
Также стоит отметить, что пересечение множеств коммутативно, то есть порядок следования множеств не влияет на результат. Таким образом, A ∩ B = B ∩ A.
При работе с большим количеством множеств можно использовать метод последовательного нахождения пересечения. Например, для трех множеств A, B и C результат будет выглядеть следующим образом: A ∩ B ∩ C = (A ∩ B) ∩ C.
Полученное пересечение может быть пустым множеством, если общих элементов нет. Например, для множеств A = {1, 2} и B = {3, 4} пересечение A и B будет равно пустому множеству: A ∩ B = {}.
Использование операции пересечения множеств позволяет решать различные задачи, связанные с нахождением общих элементов или пересечений в данных. Эта операция широко применяется в математике, логике, теории множеств и других областях.
Раздел 5: Разность множеств

Обозначение разности множеств: A \ B (читается "множество A минус множество B")
Пусть даны два множества A и B. Разность множеств A \ B = {x | x \in A и x
otin B}.
То есть, в разность множеств входят только те элементы, которые принадлежат множеству A, но не принадлежат множеству B.
Пример:
- Пусть A = {1, 2, 3, 4} и B = {3, 4, 5, 6}. Тогда A \ B = {1, 2}.
- Пусть A = {a, b, c} и B = {c, d, e}. Тогда A \ B = {a, b}.
Разность множеств также можно представить в виде диаграммы Эйлера-Венна. В этой диаграмме элементы множества A представлены кругом, элементы множества B - вложенным меньшим кругом, а элементы, принадлежащие только множеству A, обозначаются областью, которая не пересекается с меньшим кругом.
Раздел 6: Симметрическая разность множеств
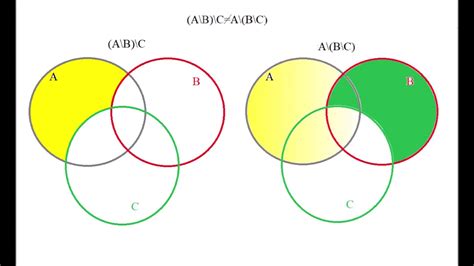
Симметрическая разность множеств можно найти с помощью следующей формулы:
A △ B = (A \ B) ∪ (B \ A)
где A \ B представляет собой разность между множеством A и множеством B, а (A \ B) ∪ (B \ A) представляет объединение двух разностей.
Например, пусть A = {1, 2, 3} и B = {2, 3, 4}. Чтобы найти симметрическую разность A △ B, мы вычтем элементы, которые присутствуют в обоих множествах, и объединим оставшиеся элементы:
A \ B = {1}
B \ A = {4}
A △ B = {1} ∪ {4} = {1, 4}
Таким образом, симметрическая разность множеств A и B равна {1, 4}.
Раздел 7: Декартово произведение множеств

Декартово произведение множеств можно представить графически с помощью таблицы, где на пересечении строки a и столбца b находится упорядоченная пара (a, b).
Например, если A = {1, 2} и B = {3, 4}, то декартово произведение A × B = {(1, 3), (1, 4), (2, 3), (2, 4)}.
Произведение множеств A × B не коммутативно, то есть A × B не всегда равно B × A. Это означает, что порядок элементов в упорядоченной паре имеет значение.
Декартово произведение множеств широко используется в математике и компьютерных науках, особенно в области комбинаторики и теории графов.
Раздел 8: Примеры операций над множествами в учебнике Мерзляка для 8 класса

В учебнике Мерзляка для 8 класса представлены различные примеры операций над множествами. При изучении данной темы ученики осваивают основные понятия операций, такие как объединение, пересечение и разность множеств.
Примеры операций над множествами в учебнике Мерзляка для 8 класса помогают ученикам понять и запомнить правила и свойства этих операций. Особое внимание уделено методу доказательства равенства множеств через включение исходных множеств в третье множество и доказательство включений в обе стороны.
В учебнике представлены примеры операций над множествами в уравнениях и неравенствах, а также в задачах на нахождение множества значений функций и отношений между элементами множеств.
- Пример операции объединения множеств: A ∪ B, где A и B - два различных множества.
- Пример операции пересечения множеств: A ∩ B, где A и B - два различных множества.
- Пример операции разности множеств: A \ B, где A и B - два различных множества.
Изучение примеров операций над множествами помогает ученикам развить навыки логического мышления и анализа. Они позволяют ученикам решать разнообразные задачи, которые требуют применения операций над множествами.
Практическое применение операций над множествами может быть найдено в различных областях, таких как комбинаторика, теория вероятностей, криптография и информатика. Поэтому изучение данной темы является важным шагом в математическом образовании.



