Если выпуклый многоугольник имеет n углов, то сумма всех его внутренних углов равна (n-2) * 180 градусов.
Эта теорема является одной из основных теорем геометрии и имеет важное значение при решении задач, связанных с многоугольниками. Она позволяет нам легко вычислять сумму внутренних углов многоугольника, зная только количество его углов.
Доказательство этой теоремы основано на принципе индукции. Базовый случай состоит из треугольника, у которого сумма всех внутренних углов равна 180 градусов. Затем предполагается, что для выпуклого многоугольника с (n-1) углами справедлива формула суммы углов. Далее, добавляется одна сторона и один угол к этому многоугольнику, и доказывается, что сумма всех углов для полученного многоугольника равна (n-1) * 180 + 180 градусов, что приводит к формуле для многоугольника с n углами.
Теорема о сумме углов выпуклого многоугольника является фундаментальным результатом геометрии и находит применение во многих областях, таких как архитектура, строительство и наука о материалах.
Что такое теорема о сумме углов выпуклого многоугольника?
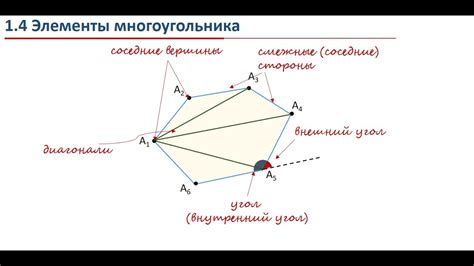
Согласно этой теореме, сумма всех внутренних углов в любом выпуклом многоугольнике равна произведению количества вершин минус два, умноженному на 180 градусов.
Теорема о сумме углов выпуклого многоугольника может быть доказана с использованием нескольких методов, включая метод индукции и метод суммирования углов внутри треугольников. Она имеет широкий спектр применений в различных областях, таких как геодезия, архитектура, компьютерная графика и другие.
Эта теорема является фундаментальной основой при изучении геометрии многоугольников и позволяет устанавливать свойства и взаимосвязи их сторон и углов. Кроме того, она позволяет упрощать вычисления и решать различные задачи, связанные с анализом и построением выпуклых многоугольников.
Теорема о сумме углов выпуклого многоугольника является одной из фундаментальных теорем в геометрии и играет важную роль в понимании свойств и связей многоугольников. Она является основой для дальнейшего изучения геометрических объектов и применяется в различных приложениях, где требуется анализ и исследование круговых и линейных структур.
Определение и применение
Это утверждение имеет широкое применение в различных областях, таких как архитектура, строительство, компьютерная графика и многие другие. Знание и понимание этой теоремы позволяет решать различные геометрические задачи и строить точные фигуры и конструкции.
Например, в архитектуре эта теорема используется для расчета углов стыковки стен и фасадов зданий. Она также помогает определить форму и размеры окон, дверей и других элементов здания, чтобы все они точно вписывались в композицию и гармонично сочетались друг с другом.
В компьютерной графике теорема о сумме углов выпуклого многоугольника используется для построения и отображения трехмерных объектов. При моделировании трехмерных форм, знание суммы углов позволяет определить правильные углы между гранями объекта и создать реалистичные и естественные изображения.
Таким образом, теорема о сумме углов выпуклого многоугольника является фундаментальным знанием в геометрии и имеет широкое применение в различных сферах человеческой деятельности, где требуется работа с фигурами, углами и пространственными конструкциями.
Формулировка теоремы
Формулировка теоремы можно записать следующим образом:
Для любого выпуклого многоугольника с n сторонами сумма всех внутренних углов равна (n-2) прямым углам:
Угол1 + Угол2 + ... + Уголn = (n-2) * 180°
Теорема о сумме углов выпуклого многоугольника является одной из основных теорем геометрии и имеет важное значение при решении задач на нахождение угловых мер или количества сторон в многоугольнике.
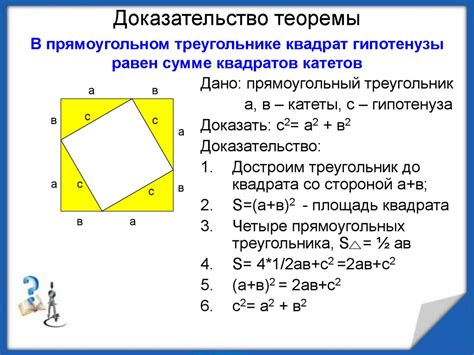
Доказательство теоремы
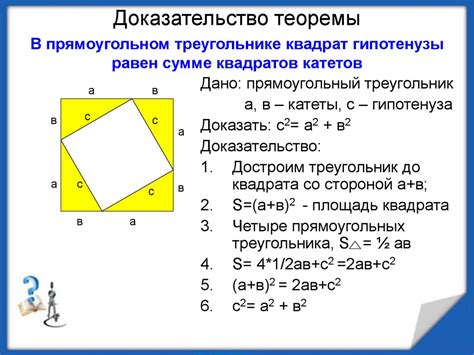
Для доказательства теоремы о сумме углов выпуклого многоугольника воспользуемся методом математической индукции.
Шаг 1: Рассмотрим случай, когда у нас есть треугольник. Очевидно, что сумма его углов равна 180 градусов.
Шаг 2: Предположим, что для многоугольника с (n-1) сторонами справедлива формула, то есть сумма его углов равна (n-2) * 180 градусов.
Шаг 3: Рассмотрим многоугольник с n сторонами. Мы можем разбить его на два многоугольника: один с (n-1) сторонами и один треугольник. Сумма углов этих двух многоугольников равна (n-2) * 180 градусов + 180 градусов, то есть n * 180 градусов.
Шаг 4: Таким образом, мы доказали, что для многоугольника с n сторонами сумма его углов равна n * 180 градусов.
Примеры и задачи с решениями

В этом разделе представлены примеры и задачи, которые помогут вам лучше понять теорему о сумме углов выпуклого многоугольника и научиться применять ее на практике.
Пример 1:
Дан выпуклый пятиугольник ABCDE. Найдите сумму всех его углов.
| Вершина | Угол |
|---|---|
| A | 120° |
| B | 90° |
| C | 135° |
| D | 100° |
| E | 115° |
Сумма углов пятиугольника равна 120° + 90° + 135° + 100° + 115° = 560°.
Пример 2:
Дан выпуклый шестиугольник ABCDEF. Найдите сумму всех его углов.
| Вершина | Угол |
|---|---|
| A | 150° |
| B | 110° |
| C | 120° |
| D | 130° |
| E | 140° |
| F | 110° |
Сумма углов шестиугольника равна 150° + 110° + 120° + 130° + 140° + 110° = 760°.
Задача:
Дан выпуклый восьмиугольник ABCDEFGH. Найдите сумму всех его углов, если известны следующие углы:
| Вершина | Угол |
|---|---|
| A | 140° |
| B | 120° |
| C | 110° |
| D | 130° |
| E | 125° |
| F | 150° |
| G | 115° |
| H | 145° |
Сумма углов восьмиугольника равна 140° + 120° + 110° + 130° + 125° + 150° + 115° + 145° = 1155°.
Теперь вы можете применять теорему о сумме углов выпуклого многоугольника для решения разных задач по геометрии.



