Биссектриса внешнего угла треугольника – это линия, которая делит данный угол на два равных угла. Важно отметить, что внешний угол треугольника образуется продолжением одной из его сторон. Это значит, что для нахождения биссектрисы внешнего угла нужно провести линию из вершины треугольника, которая будет пересекать продолжение этой стороны и делить угол на две равные части.
Существует несколько способов доказательства того, что проведенная линия действительно является биссектрисой внешнего угла. Один из таких способов основывается на теореме о внутренней и внешней сумме углов треугольника. Согласно этой теореме, сумма внутренних углов треугольника равна 180 градусов. Если мы проведем линию, которая разделит внешний угол треугольника на два равных угла, то сумма этих углов будет равна половине внутреннего угла треугольника, то есть 90 градусов. Таким образом, мы доказываем, что проведенная линия является биссектрисой внешнего угла треугольника.
Примером применения биссектрисы внешнего угла треугольника может служить задача на нахождение расстояния от вершины до точки пересечения продолжений двух сторон треугольника. Проведя биссектрису внешнего угла, мы получим два равных треугольника. Зная длины сторон этих треугольников, можно применить теорему Пифагора для нахождения расстояния между вершиной и точкой пересечения продолжений сторон. Таким образом, использование биссектрисы внешнего угла треугольника позволяет решить данную задачу и получить точный результат.
Основные теоремы о биссектрисе внешнего угла треугольника
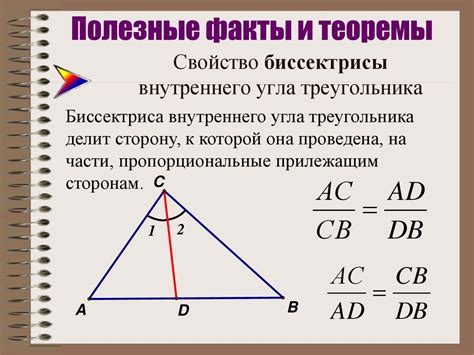
Биссектриса внешнего угла треугольника проходит через одну из вершин треугольника и делит противоположную сторону на две сегменты, пропорциональные двум оставшимся сторонам.
Изучая свойства биссектрисы внешнего угла треугольника, мы можем сформулировать несколько основных теорем:
| Теорема 1: | Биссектриса внешнего угла треугольника делит противоположную сторону на отрезки, пропорциональные двум оставшимся сторонам. |
| Теорема 2: | Биссектриса внешнего угла треугольника является вспомогательной линией при доказательстве различных свойств треугольника. |
| Теорема 3: | Сумма измерений внешнего исходного угла треугольника и внешнего вспомогательного угла, образованного биссектрисой, равна 180 градусам. |
Приведем пример использования этих теорем:
Дан треугольник со сторонами a = 5 см, b = 7 см и c = 8 см. Найдем длину сегмента, на который биссектриса внешнего угла треугольника pq делит противоположную сторону.
Из теоремы 1 следует:
| a : p = c : q |
| 5 : p = 8 : q |
| 5q = 8p |
Аналогично, из теоремы 1 можно получить:
| b : r = c : q |
| 7 : r = 8 : q |
| 7q = 8r |
Из этих двух уравнений можно составить систему уравнений и найти значения p и r.
Таким образом, основные теоремы о биссектрисе внешнего угла треугольника играют важную роль в геометрии, а их применение позволяет решать разнообразные задачи, связанные с треугольниками и их свойствами.
Роль биссектрисы внешнего угла треугольника
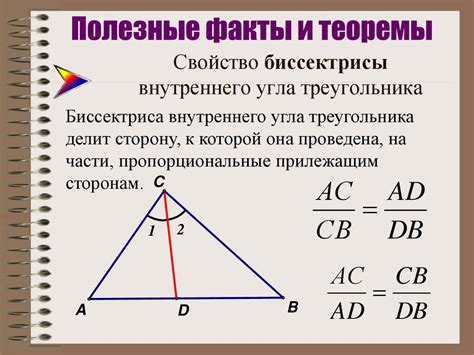
Одной из главных функций биссектрисы внешнего угла является то, что она определяет равные углы между внешней стороной треугольника и продолжениями его сторон. Это позволяет легко находить меру отсутствующих углов или использовать их для дальнейших геометрических вычислений.
Другой важной ролью биссектрисы внешнего угла является то, что она является местом пересечения трех биссектрис внешних углов треугольника. Это означает, что точка пересечения биссектрис будет центром вписанной окружности, которая касается всех сторон треугольника.
Пример: Рассмотрим треугольник ABC. Биссектриса внешнего угла C, которая проходит через точку D, делит угол C на две равные части, CJ и CK. Она также пересекается с продолжением стороны AB и образует точку H.
Теорема: Угол HCB равен углу ACD.
Доказательство этой теоремы основано на свойствах углов, параллельных и пересекающихся линий. Поэтому, зная значения угла HCB и угла HCA, мы можем вычислить и меру угла ACD.
Таким образом, биссектриса внешнего угла треугольника играет непосредственную роль в геометрических вычислениях и определении соотношений между углами треугольника. Это помогает упростить геометрические задачи и сделать их более доступными для решения.
Первая теорема о биссектрисе внешнего угла
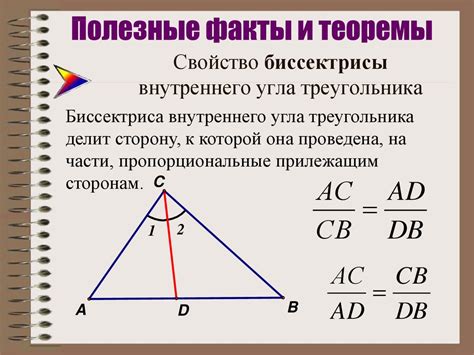
Первая теорема о биссектрисе внешнего угла утверждает, что любая биссектриса внешнего угла треугольника делит противолежащую сторону в отношении, равном отношению других двух сторон этого треугольника.
То есть, пусть у нас есть треугольник ABC, внешний угол ACD и биссектриса AD. Тогда отношение длины отрезка CD к длине отрезка BD будет равно отношению длины стороны AC к длине стороны AB.
Это можно записать следующим образом:
CD/BD = AC/AB
Доказательство данной теоремы основано на свойствах биссектрисы и пропорциональности. Подробное рассмотрение и доказательство данной теоремы позволяют легче разобраться в ее сути и использовать ее в дальнейших геометрических рассуждениях и задачах.
Пример:
Рассмотрим треугольник ABC, в котором BC = 10 см, AC = 8 см, AB = 6 см. Пусть AD - биссектриса внешнего угла ACD. Найдем отношения длины отрезка CD к длине отрезка BD.
Используя первую теорему о биссектрисе внешнего угла, мы можем записать:
CD/BD = AC/AB = 8/6 = 4/3
Учитывая, что BC = 10 см, мы можем выразить длину каждого из отрезков:
CD = (4/3) * BD
BD + CD = BC
BD + (4/3) * BD = 10
BD(1 + 4/3) = 10
BD(7/3) = 10
BD = 30/7 см
Таким образом, длина отрезка CD равна (4/3) * (30/7) = 40/7 см, а длина отрезка BD равна 30/7 см.
Таким образом, первая теорема о биссектрисе внешнего угла позволяет находить неизвестные длины сторон и отрезков в треугольнике, а также использовать их в доказательствах и решении геометрических задач.
Доказательство первой теоремы о биссектрисе внешнего угла
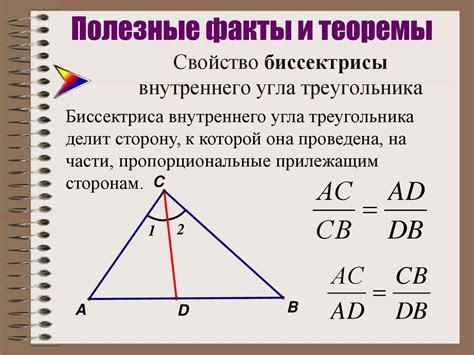
Первая теорема о биссектрисе внешнего угла гласит: Биссектриса внешнего угла треугольника делит противоположную сторону в отношении длин остальных двух сторон.
Рассмотрим треугольник ABC, где CD - биссектриса угла ADC, D - точка пересечения биссектрисы и прямой BC.
Для доказательства теоремы применим угловые и сторонние равенства:
1. Угол ADC равен сумме углов ACD и DCA по свойству угла, деленного биссектрисой.
2. Угол ACD и углы треугольника ABC смежны, поэтому угол ACD равен полусумме углов ABC и ACB.
3. Угол ADC и угол ABC являются вертикальными углами и поэтому равны.
4. Из равенства углов ADC и ABC следует равенство полусумм углов ABC и ACB и углом DCA.
Зная, что сумма углов треугольника равна 180 градусам, мы можем записать уравнение:
(ABC + ACB)/2 + DCA = ADC
Также, имея в виду, что AD делит угол ADC пополам, мы можем записать:
ADC = (ABC + ACB)/2
Заметим, что (ABC + ACB)/2 + DCA и (ABC + ACB)/2 равны друг другу, поскольку они равны ADC. Из этого следует, что DCA равен нулю, так как сумма двух равных углов равна нулю.
Таким образом, мы доказали, что DCA равно нулю, и, следовательно, угол ADC и углы ABC и ACB делятся биссектрисой так, что BD/DC = AB/AC.
Вторая теорема о биссектрисе внешнего угла
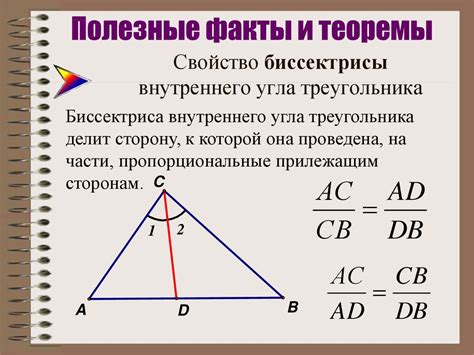
Вторая теорема о биссектрисе внешнего угла гласит:
Биссектриса внешнего угла треугольника делит противолежащую сторону в отношении, равном отношению длины ближайшего замыкающего угла к длине противоположного замыкающего угла.
Другими словами, пусть дан треугольник ABC, в котором угол CDA - внешний угол по отношению к треугольнику ABC. Тогда биссектриса угла CDA делит сторону AB в отношении, равном отношению угла CDB к углу CBA.
Эта теорема очень полезна при решении геометрических задач и позволяет определять отношения длин сторон треугольника с использованием его углов.
Пример:
Пусть дан треугольник ABC, в котором угол CAB равен 40 градусам, угол ABC равен 60 градусам. Зная, что биссектриса угла CAB делит сторону BC в отношении 2:3, найдем отношение длин сторон AB и AC.
- Отношение длин углов CDB и CBA равно 2:3.
- Так как угол CBA равен 60 градусам, тогда угол CDB равен 40 градусам.
- Таким образом, отношение длин сторон AB и AC также равно 2:3, и можно сказать, что сторона AB в 2 раза короче стороны AC.
Таким образом, с использованием второй теоремы о биссектрисе внешнего угла мы можем находить отношения длин сторон треугольника и решать различные геометрические задачи.
Доказательство второй теоремы о биссектрисе внешнего угла
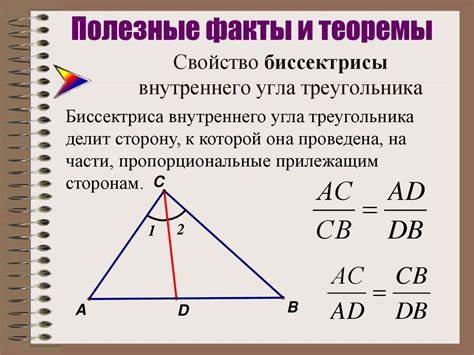
Докажем, что BD - также является биссектрисой угла В, то есть делит его на две равные части.
Из построения треугольника АВС, угол CBА равен сумме углов CBA и BAC. Значит, угол CBА больше угла CBA.
Орисуем отрезок BF (построение) так что BF ≡ BD и угол FBC равен углу BAC.
Тогда имеем углы FBA и ABC являются соответственно внутренними углами треугольника АСВ, где прямая AF является биссектрисой внутреннего угла BAC.
Так как углы ABC и СBA в одном треугольнике будут быть равными, имеем
ABF ≡ CBF
Но угол ABF и CBF с соответственными углами BAC и CBA равен, следовательно имеет место
BF равен BD
и оба отрезка AB и CB равноудалены от нашей точки D, что означает, что точка В принадлежит биссектрисе угла СBD, а значит, угол СBD делится этой биссектрисой на две равные части.
Таким образом, доказано, что вторая биссектриса внешнего угла треугольника делит его на две равные части.
Примеры применения теорем о биссектрисе внешнего угла
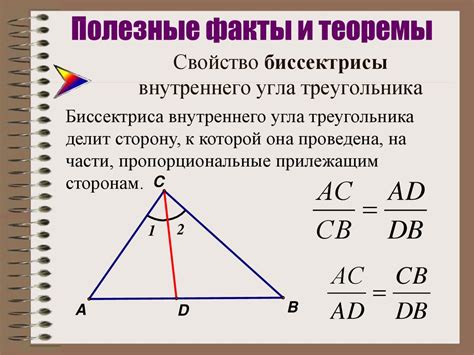
Теоремы о биссектрисе внешнего угла треугольника играют важную роль в геометрии и различных областях науки, инженерии и архитектуры. Вот несколько примеров их применения:
- В навигации. Теоремы о биссектрисе внешнего угла позволяют определить точное направление судна или летательного аппарата относительно вертикальной оси. Это помогает пилотам и навигаторам правильно управлять и назначать курсы.
- В архитектуре. Теоремы о биссектрисе внешнего угла используются для расчета угловых размеров зданий. Архитекторы могут точно определить угол наклона стены или крыши, чтобы обеспечить конструкцию с правильной противоположной биссектрисе.
- В мебельном производстве. Теоремы о биссектрисе внешнего угла применяются в процессе изготовления мебели с угловыми деталями. Это позволяет точно определить углы, необходимые для сборки и сращивания, обеспечивая прочность и правильное соединение деталей мебели.
- В геодезии. Теоремы о биссектрисе внешнего угла используются для измерения расстояния до удаленных объектов и определения их координат. При помощи оптических инструментов и математических вычислений геодезисты могут точно измерить углы и расстояния, что помогает в создании карт и определении географического положения объектов.
Это лишь несколько примеров применения теорем о биссектрисе внешнего угла треугольника. Видно, что эти теоремы имеют широкий спектр применений и играют важную роль в различных областях науки и техники.



