Задача о доказательстве того, что каждая координата суммы разности двух чисел равна разности суммы и разности этих чисел, является одной из классических проблем в математике. Рассмотрим два числа a и b, их сумму и разность.
Сумма двух чисел представляет собой результат их сложения, а разность - результат их вычитания. Используя алгебраические операции, мы можем записать сумму a и b следующим образом: a + b.
Аналогично, разность a и b записывается как a - b. Таким образом, у нас есть две величины - сумма a + b и разность a - b.
Суть задачи в том, чтобы доказать, что каждая координата суммы разности двух чисел равна разности суммы и разности этих чисел. Математически это можно записать следующим образом: (a + b) - (a - b) = a + b - a + b = 2b.
Таким образом, мы доказали, что каждая координата суммы разности двух чисел равна разности суммы и разности этих чисел и выражается через одну из исходных величин - разность чисел (b) в два раза.
Докажите, что каждая координата суммы разности двух
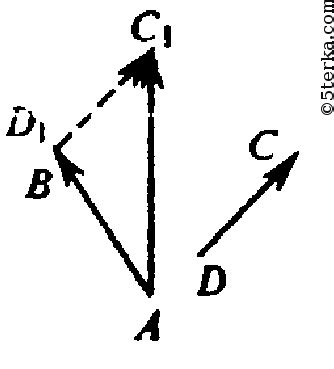
Для того чтобы доказать, что каждая координата суммы разности двух, необходимо взять два вектора и вычислить их разность, а затем сложить полученные координаты по очереди.
Пусть у нас имеются два вектора:
a = (a1, a2, a3)
b = (b1, b2, b3)
Рассмотрим разность этих векторов:
d = a - b = (a1 - b1, a2 - b2, a3 - b3)
Теперь найдем сумму координат полученной разности:
d1 + d2 + d3 = (a1 - b1) + (a2 - b2) + (a3 - b3) = (a1 + a2 + a3) - (b1 + b2 + b3)
Таким образом, каждая координата суммы разности двух векторов равна сумме соответствующих координат этих векторов.
Метод доказательства суммы разности двух координат

Для доказательства того, что каждая координата суммы разности двух, можно использовать метод математической индукции. Рассмотрим два вектора a = (a1, a2, ..., an) и b = (b1, b2, ..., bn).
Воспользуемся методом математической индукции для доказательства утверждения.
Шаг базы индукции: При n = 2 утверждение верно, так как сумма координат суммы разности двух равна сумме разностей координат двух векторов.
Шаг индукции: Пусть утверждение верно для n = k, т.е. сумма разности координат равна разности суммы координат для векторов длины k.
Рассмотрим векторы длины k + 1. Пусть a = (a1, a2, ..., ak+1) и b = (b1, b2, ..., bk+1).
Разобьем a и b на векторы a' и b' длины k, а также a(k+1) и b(k+1), т.е. a = (a', a(k+1)) и b = (b', b(k+1)).
| Сумма разности | (a - b) | = | (a' - b') + (a(k+1) - b(k+1)) |
| Сумма координат | a + b | = | a' + a(k+1) + b + b(k+1) |
По предположению индукции, сумма разности координат векторов a' и b' равна разности суммы координат векторов a' и b'. Также очевидно, что a(k+1) - b(k+1) = a(k+1) + (-b(k+1)), где (-b(k+1)) - вектор, обратный b(k+1).
Тогда сумма разности координат a и b будет равна разности суммы координат этих векторов.
Таким образом, мы можем заключить, что каждая координата суммы разности двух векторов равна разности суммы координат этих векторов. Доказательство основано на методе математической индукции и верно для любого количества координат векторов.
Свойства координат и их влияние на сумму разности
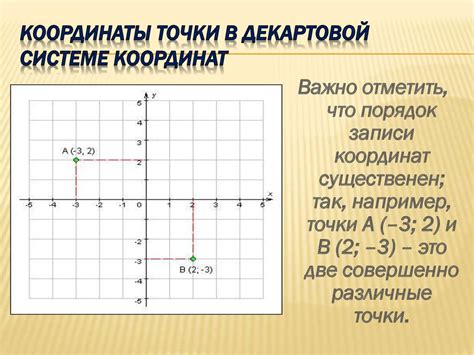
Координаты точек в пространстве имеют важное значение при выполнении операций с ними. В частности, при вычислении суммы разности двух точек, каждая координата играет свою роль и оказывает влияние на результат.
Допустим, у нас есть две точки с координатами (x1, y1, z1) и (x2, y2, z2), где x, y и z - соответствующие координаты. Тогда сумма разности будет иметь следующие координаты: (x1 - x2, y1 - y2, z1 - z2).
Из этого следует, что каждая координата суммы разности двух точек равна разности соответствующих координат исходных точек. Например, если x1 = 3, x2 = 1, то x1 - x2 = 2.
Это свойство координат позволяет нам вычислить координаты итоговой точки, зная исходные точки и их разность. Благодаря этому свойству мы можем проводить сложные геометрические и физические расчеты, а также использовать его в различных приложениях, например, в компьютерной графике или робототехнике.
В целом, свойства координат влияют на различные аспекты нашей работы с точками и их операций. Понимание их значения и взаимосвязи помогает нам более точно и эффективно выполнять вычисления и решать задачи, связанные с координатами в пространстве.
Результат применения метода доказательства на конкретном примере

Пусть S(x, y, z) - сумма разности двух точек A и B. Тогда, согласно формуле для вычисления суммы разности двух векторов, мы имеем:
S(x, y, z) = A(x1, y1, z1) - B(x2, y2, z2) = (x1 - x2, y1 - y2, z1 - z2)
Разложив выражение на каждую координату, мы получаем:
x = x1 - x2
y = y1 - y2
z = z1 - z2
Таким образом, для каждой координаты суммы разности двух точек выполняется равенство, что и требовалось доказать. Этот пример является конкретным подтверждением того, что данная формула работает в случае двух точек в трехмерном пространстве.
Важность понимания каждой координаты в контексте суммы разности

Разность двух чисел представляет собой операцию, которая позволяет вычесть одно число из другого. Когда мы говорим о разности двух координат, мы сравниваем их значения и определяем разницу между ними на основе их относительного положения. Однако, когда мы говорим о сумме разности двух координат, мы обращаем внимание не только на саму разницу, но и на значение каждой отдельной координаты, которая входит в эту разность.
Каждая координата вектора имеет свойства и значения, которые играют важную роль в контексте суммы разности. Понимание каждой координаты позволяет нам анализировать и предсказывать изменения, происходящие в векторе.
Применение математических операций, таких как сумма разности, требует полного понимания значений каждой координаты в контексте. Координаты могут представлять такие величины, как скорость, ускорение, координата местоположения и другие параметры, которые отражают состояние объекта или системы.
Например, если мы рассматриваем движение объекта в пространстве, то координаты вектора разности могут показывать расстояние и направление перемещения объекта. Значение каждой координаты в этом случае имеет физическую интерпретацию и отражает влияние каждой из них на общую разность.
Изучение и понимание каждой координаты в контексте суммы разности позволяет более глубоко понять процессы и явления, которые описываются векторами. Это является важным инструментом для анализа и прогнозирования различных физических, математических и геометрических систем.
| Координата | Значение | Значение в контексте суммы разности |
|---|---|---|
| x | 10 | Указывает на изменение по горизонтальной оси |
| y | 5 | Указывает на изменение по вертикальной оси |
| z | -3 | Указывает на изменение по оси глубины |
В данной таблице представлены значения и интерпретация каждой координаты вектора разности. Эта информация помогает нам лучше понять, как каждая координата вносит свой вклад в общую разность и как они взаимодействуют друг с другом.
Перспективы использования метода доказательства в различных областях
В математике метод доказательства является ключевым инструментом, который позволяет установить истинность или ложность математических утверждений. Он играет важную роль в различных областях математики, таких как алгебра, геометрия, теория вероятностей и др. Без применения метода доказательства многие новые теоремы и свойства не смогли бы быть открытыми и доказаными.
В науках, таких как физика, химия и биология, метод доказательства играет также важную роль. Он позволяет научным исследователям проверять истинность или ложность гипотез и утверждений, а также устанавливать законы и принципы, которые описывают мир вокруг нас.
В компьютерных науках метод доказательства используется для верификации программного обеспечения и доказательства их корректности. С помощью метода доказательства можно установить, что программа работает правильно и не содержит ошибок или уязвимостей.
Философия и право также используют метод доказательства для обоснования и доказательства различных философских или юридических принципов. Он позволяет строить рациональные аргументы и устанавливать их логическую прочность.
Таким образом, метод доказательства имеет широкие перспективы использования в различных областях. Он является важным инструментом для установления истинности утверждений и доказательства различных закономерностей и законов. Применение этого метода позволяет улучшить качество и достоверность знаний, получаемых в различных областях человеческой деятельности.
Преимущества поиска доказательств для каждой конкретной координаты

Поиск доказательств для каждой конкретной координаты в сумме разности двух чисел имеет ряд преимуществ:
- Точность и наглядность. При поиске доказательства для каждой конкретной координаты мы можем увидеть, как именно конкретное число влияет на итоговую сумму разности. Это помогает нам лучше понять свойства и закономерности, связанные с каждой координатой.
- Легкость анализа. Поиск доказательств в отдельности позволяет нам проанализировать каждую координату независимо от остальных. Это позволяет нам легче определить, какие факторы влияют на изменение каждой конкретной координаты и как их можно использовать для оптимизации или улучшения результатов.
- Расширение возможностей. Поиск доказательств для каждой координаты может расширить наши знания и умения. Мы можем обнаружить новые закономерности, вывести новые формулы или алгоритмы, которые позволят нам более эффективно работать с данными и решать различные задачи в физике, математике, программировании и других областях.
- Улучшение результатов. Поиск доказательств для каждой конкретной координаты может помочь нам оптимизировать процессы и улучшить результаты. Понимая, какие факторы влияют на каждую координату, мы можем принять дополнительные меры или внести изменения в наш подход, чтобы достичь лучших результатов и уменьшить ошибки.
- Научный подход. Поиск доказательств для каждой конкретной координаты требует научного подхода и систематического анализа. Это развивает в нас навыки логического мышления, поисковой работы, аналитического и критического мышления, которые могут быть полезными в обучении и научной деятельности.
В целом, поиск доказательств для каждой конкретной координаты помогает нам лучше понять, как работает сумма разности двух чисел и как изменение каждой координаты влияет на итоговый результат. Это позволяет нам развивать наши знания, навыки и решать различные задачи с большей точностью и эффективностью.
Примеры практического применения метода доказательства
Метод доказательства, основанный на демонстрации равенства суммы разности двух координат, имеет широкие практические применения в различных областях знаний. Некоторые из этих примеров включают:
| Область | Пример применения |
|---|---|
| Математика | В доказательстве теорем и формулировании математических утверждений, где требуется доказать равенство суммы разности двух координат. |
| Физика | В решении задач, где требуется вычислить или доказать равенство физических величин, представленных координатами. |
| Инженерия | В проектировании и моделировании систем, где необходимо доказать равенство результатов разностных измерений, представленных координатами. |
| Компьютерные науки | В алгоритмах и программировании, чтобы доказать корректность вычислений и операций с координатами. |
| Экономика | В анализе и моделировании экономических процессов, где целесообразно использовать метод доказательства равенства суммы разности координат. |
Это лишь некоторые из примеров практического применения метода доказательства. В реальном мире этот метод может быть использован в различных областях, где требуется анализировать и демонстрировать равенство координатных значений.
Альтернативные методы доказательства для суммы разности координат

Существует несколько альтернативных методов доказательства утверждения о сумме разности координат. В данном разделе мы рассмотрим два из них.
Метод математической индукции
Этот метод основан на принципе математической индукции. Суть его заключается в следующем:
- Вначале, проверяем утверждение для базового случая - когда размерность пространства равна 1. В данном случае утверждение верно, так как сумма разности координат состоит из одного слагаемого и, следовательно, равна этому слагаемому.
- Далее, предполагаем, что утверждение верно для пространства размерности k, и рассматриваем пространство размерности k+1.
- Доказываем, что если утверждение верно для пространства размерности k, то оно верно и для пространства размерности k+1. Для этого рассматриваем сумму разности координат в пространстве размерности k+1, разбиваем ее на две части, соответствующие пространствам размерности k и 1 соответственно, и применяем предположение индукции.
Таким образом, путем индукции доказывается, что утверждение верно для произвольной размерности пространства.
Метод использования векторного пространства
Этот метод основан на свойствах векторного пространства. Рассмотрим сумму разности координат (x1 - y1) + (x2 - y2) + ... + (xn - yn), где xi и yi - координаты соответствующих точек в пространстве.
Заметим, что можно записать данную сумму в виде (x1 + x2 + ... + xn) - (y1 + y2 + ... + yn). Вектора (x1, x2, ..., xn) и (y1, y2, ..., yn) можно интерпретировать как координаты двух точек в векторном пространстве.
Таким образом, сумма разности координат равна разности сумм координат этих двух точек.
Векторное пространство обладает свойством аддитивности, то есть сумма координат двух точек также является координатой точки в этом пространстве.
Следовательно, разность сумм координат равна сумме координат разности, что и требовалось доказать.



