Правильные многоугольники всегда привлекали внимание ученых и любителей геометрии. Они обладают множеством интересных свойств и теорем, которые можно доказывать и изучать на протяжении долгих веков. Одним из таких свойств является радиус вектора центра правильного многоугольника.
Радиус вектора центра правильного многоугольника является отрезком, соединяющим центр многоугольника с одной из его вершин. Этот отрезок имеет ряд интересных свойств, одно из которых заключается в том, что радиус вектора имеет одинаковую длину для всех вершин правильного многоугольника.
Доказательство этого факта основывается на анализе геометрических свойств многоугольника. Изначально, начнем с определения правильного многоугольника - это многоугольник, у которого все стороны и углы равны между собой. Пусть у нас есть правильный многоугольник со сторонами длины a и n углами.
Понятие радиуса вектора
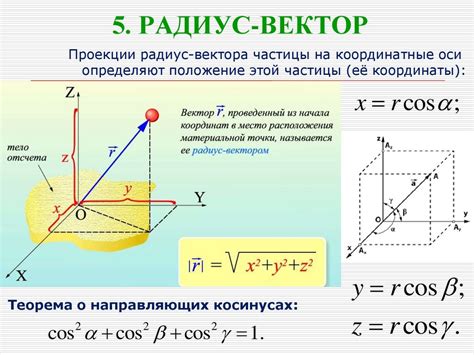
|r| = sqrt(x^2 + y^2 + z^2)
где sqrt - корень извлекаемый.
Радиус вектор может быть представлен в виде упорядоченной тройки чисел (x, y, z).
Радиус вектор используется для описания положения точек в пространстве, а также в различных физических и математических задачах. Он позволяет задать направление и длину, и является важным понятием в векторной алгебре и геометрии.
Правильный многоугольник
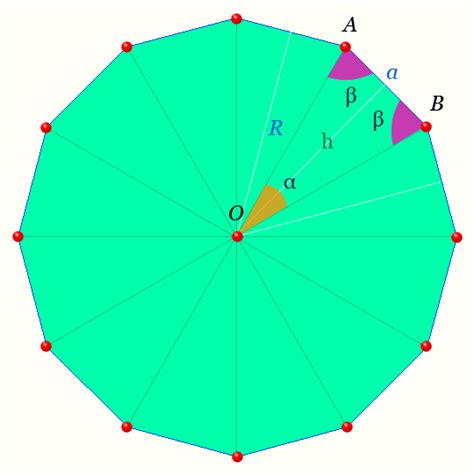
В правильном многоугольнике каждая сторона имеет одинаковую длину, а каждый угол имеет одинаковую величину. Число сторон правильного многоугольника называется его порядком или количеством углов. Например, правильный треугольник имеет порядок 3, правильный четырехугольник - порядок 4, и так далее.
Круг является особым случаем правильного многоугольника, где порядок многоугольника равен бесконечности. В круге все стороны и углы равны между собой, но величина каждого угла и длина каждой стороны бесконечная.
Правильные многоугольники имеют множество интересных свойств и связей, которые изучаются в геометрии. Они часто встречаются в различных областях науки, искусства и архитектуры, и вызывают удивление своей симметрией и гармонией. Изучение правильных многоугольников помогает лучше понять геометрию и её применение в практических задачах.
Свойства правильного многоугольника
- Углы правильного многоугольника равны. Все внутренние углы правильного многоугольника равны, и их величина вычисляется по формуле: 180 * (n-2) / n, где n - количество сторон многоугольника.
- Сумма внутренних углов правильного многоугольника равна 180 * (n-2) градусов, где n - количество сторон многоугольника. Доказательство этого свойства основано на делении многоугольника на треугольники с вершинами в центре и на его сторонах.
- Диагонали правильного многоугольника равны. Диагонали - это отрезки, соединяющие любые две несоседние вершины многоугольника. В правильном многоугольнике количество диагоналей равно n * (n-3) / 2, где n - количество сторон многоугольника.
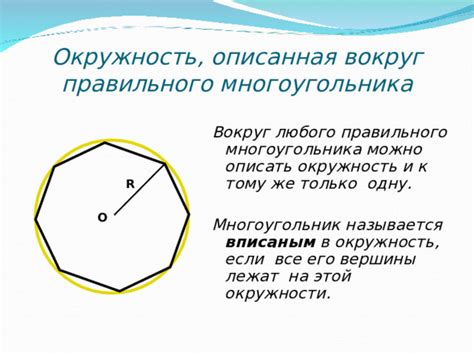
- Радиус описанной окружности правильного многоугольника равен расстоянию от центра многоугольника до любой его вершины. Радиус описанной окружности можно найти по формуле: R = s / (2 * sin(180 / n)), где R - радиус описанной окружности, s - длина стороны многоугольника, n - количество сторон многоугольника.
- Радиус вписанной окружности правильного многоугольника равен половине расстояния между центром многоугольника и любой его стороной. Радиус вписанной окружности можно найти по формуле: r = s / (2 * tan(180 / n)), где r - радиус вписанной окружности, s - длина стороны многоугольника, n - количество сторон многоугольника.
Эти свойства позволяют установить взаимосвязь между различными параметрами и размерами правильного многоугольника, что может быть полезно при его изучении и решении геометрических задач.
Доказательство равенства радиусов векторов центра и вершины правильного многоугольника
- Правильный многоугольник имеет все стороны одинаковой длины и все углы равны.
- Центр многоугольника O равноудален от всех его вершин, поскольку все стороны одинаковой длины.
- Это означает, что радиус вектора OA равен радиусу вектора OX для любой вершины X многоугольника.
Таким образом, доказано равенство радиусов векторов центра и вершины правильного многоугольника, так как центр многоугольника O равноудален от всех его вершин.
Символическое обозначение радиуса вектора
Радиус вектор центра правильного многоугольника обычно обозначается символом R.
В математике и физике радиус вектор используется для описания положения точки или объекта в пространстве относительно начала координат. Он представляет собой вектор, который соединяет начало координат с заданной точкой или объектом.
Для правильного многоугольника радиус вектор является вектором, проведенным от начала координат до центра многоугольника. Поскольку правильный многоугольник имеет все стороны и углы равными, радиус вектор имеет фиксированную длину и указывает направление от начала координат к центру многоугольника.
Обозначение радиуса вектора символом R обычно делает его более удобным для записи и использования в математических выражениях. Вместе с координатами точек или объектов, радиус вектор помогает определить их положение и движение в пространстве.
Геометрическое представление радиуса вектора

Радиус вектора представляет собой вектор, соединяющий начало координат (точку O) с любой точкой в пространстве. Он характеризуется длиной, направлением и положением в пространстве.
Для правильного многоугольника радиус вектор описывает путь от центра многоугольника до его вершины. В случае правильного многоугольника, радиусы векторы имеют одинаковую длину и направление.
Геометрически, радиус вектор представляет собой линию, которая соединяет центр правильного многоугольника с его вершиной. Эта линия имеет одно и то же направление и одинаковую длину для всех вершин многоугольника.
Радиус вектор является основным элементом для доказательства свойств правильного многоугольника. Он позволяет определить положение вершин многоугольника относительно его центра и установить геометрические связи между ними.
Важно отметить, что радиус вектор представляет собой векторную величину, что означает, что он имеет не только длину, но и направление. Поэтому при работе с радиусами векторами необходимо учитывать их ориентацию и взаимное расположение.
Доказательство совпадения радиусов векторов

Доказательство совпадения радиусов векторов в контексте правильного многоугольника связано с использованием геометрических свойств и определений.
Предположим, у нас есть правильный многоугольник с центром в точке O и радиусом r. Пусть A и B - две произвольные вершины этого многоугольника. Мы хотим доказать, что векторы OA и OB имеют одинаковую длину.
1. Доказательство с использованием косинусов
Для начала, построим радиусы векторов OA и OB. Так как многоугольник правильный, то угол AOB будет равен 360 градусов, поскольку это сумма всех углов многоугольника.
Мы можем использовать формулу косинуса, чтобы выразить длины векторов OA и OB через угол AOB:
OA² = r² + r² - 2r · r · cos(AOB)
OA² = 2r² - 2r² cos(AOB)
OA² = 2r² (1 - cos(AOB))
Аналогично, для вектора OB:
OB² = 2r² (1 - cos(AOB))
Таким образом, мы получаем, что длина вектора OA равна длине вектора OB, так как оба вектора имеют одинаковые составляющие и косинус AOB равен 1 при правильном многоугольнике.
2. Доказательство с использованием подобия треугольников
Мы можем также использовать подобие треугольников, чтобы доказать равенство длин векторов OA и OB.
Из центра O проведем перпендикуляры к отрезкам OA и OB, обозначим их длинами h₁ и h₂ соответственно.
Так как многоугольник правильный, то углы OAH₁ и OBH₂ прямые. Тогда треугольники OAH₁ и OBH₂ будут подобными.
Так как у этих подобных треугольников соответственные стороны пропорциональны, получаем:
OA / h₁ = OB / h₂
Умножим обе части на h₁ и h₂:
OA = (h₁ / h₂) · OB
Так как h₁ и h₂ - это высоты треугольников OAH₁ и OBH₂, то они равны и можно записать:
OA = OB
Таким образом, мы также доказали равенство длин векторов OA и OB с использованием подобия треугольников.
В обоих доказательствах мы получили, что для правильного многоугольника радиусы векторов, исходящих из центра этого многоугольника, совпадают.
Доказательство, что радиус вектора центра правильного многоугольника совпадает с суммой радиусов векторов вершин

Для того чтобы доказать данное утверждение, рассмотрим правильный многоугольник с центром в точке O. Пусть его радиус равен R, а количество вершин равно n. Обозначим вершины многоугольника как A1, A2, ..., An.
Поскольку многоугольник правильный, все стороны и углы между ними равны. Таким образом, радиусы векторов вершин многоугольника являются радиусами окружности, описанной вокруг многоугольника.
Чтобы доказать, что радиус вектора центра O совпадает с суммой радиусов векторов вершин, достаточно рассмотреть треугольник OAB1. Он имеет сторону длиной R и угол при вершине A1 равным 360°/n.
По теореме синусов:
| OA1 / sin(360°/n) | = AB1 / sin ∠OAB1 |
| OA1 | = AB1 * sin(360°/n) / sin ∠OAB1 |
| OA1 | = R * sin(360°/n) / sin ∠OAB1 |
Так как у многоугольника все стороны и углы равны, то ∠OAB1 равен 360°/n. При этом, sin(360°/n) / sin(360°/n) равно 1. Таким образом, получаем:
OA1 = R * sin(360°/n) / sin(360°/n) = R
Аналогичное рассуждение можно провести для каждой вершины многоугольника. Следовательно, радиус вектора центра O совпадает с суммой радиусов векторов вершин многоугольника, что и требовалось доказать.
Обозначение радиусов векторов вершин
При изучении радиуса вектора центра правильного многоугольника, каждая вершина многоугольника может быть обозначена с помощью радиуса вектора, который представляет собой вектор, начинающийся в начале координат и направленный к данной вершине.
Для обозначения радиусов векторов вершин в математике обычно используется прописная буква R, с индексом, обозначающим номер вершины. Например, R1, R2, R3 и т.д.
Таким образом, R1 обозначает радиус вектор первой вершины, R2 - радиус вектор второй вершины и так далее.
Используя эти обозначения, мы можем легко обращаться к каждому радиусу вектору вершины и изучать их свойства и взаимосвязи в контексте доказательства радиуса вектора центра правильного многоугольника.
Геометрическое представление радиусов векторов вершин

Рассмотрим правильный многоугольник с центром в начале координат. Вершины многоугольника расположены равномерно на окружности с радиусом R. Для каждой вершины с номером i можно определить радиус вектор ri.
Геометрическое представление радиусов векторов вершин также называется геометрическим построением радиусов. Оно заключается в следующем:
1. Найдем произвольную вершину многоугольника, например, вершину с номером 1. Ее радиус вектор обозначим как r1.
2. Затем найдем радиус вектор вершины с номером 2, который обозначим как r2.
Чтобы построить r2, проведем линию, параллельную r1, отложим на ней отрезок длиной R (равный радиусу многоугольника), начиная от конца r1, и соединим конец этого отрезка с началом координат. Получим вектор r2.
3. Аналогично построим радиус вектор вершины с номером 3, соединив конец вектора r2 с началом координат. Результатом будет радиус вектор r3.
Продолжим данное построение для каждой вершины многоугольника.
Таким образом, геометрическое представление радиусов векторов вершин дает возможность наглядно представить, как расположены вершины правильного многоугольника относительно его центра и начала координат.
Доказательство равенства радиусов векторов центра и вершин

Для доказательства равенства радиусов векторов центра и вершин в правильном многоугольнике, нам необходимо воспользоваться геометрическими свойствами фигуры.
Возьмем произвольную вершину многоугольника и проведем ее радиус вектор – отрезок, соединяющий центр многоугольника с этой вершиной.
Так как многоугольник является правильным, он имеет все стороны и углы равными. Это означает, что все его радиусы векторов равны между собой.
Для доказательства равенства радиусов векторов центра и вершин можно также воспользоваться свойством равнобедренного треугольника. Точка пересечения радиуса вектора и стороны многоугольника является основанием равнобедренного треугольника.
Равнобедренный треугольник имеет одинаковые основания и равные боковые стороны. В нашем случае, основание треугольника – сторона многоугольника, а боковые стороны – радиус вектор и сторона многоугольника.
Таким образом, радиус вектор центра и радиус вектор вершины являются боковыми сторонами равнобедренного треугольника, а значит, они равны.
Таким образом, мы доказали равенство радиусов векторов центра и вершин правильного многоугольника.



