В математике существует понятие счетности множества, которое означает, что элементы этого множества можно упорядочить таким образом, что каждому элементу будет соответствовать натуральное число. Например, множество всех натуральных чисел является счетным, так как его элементы можно упорядочить по возрастанию.
Однако, что происходит, когда нужно объединить два счетных множества? В данной статье мы рассмотрим доказательство того, что объединение двух счетных множеств также является счетным.
Предположим, что у нас есть два счетных множества A и B. Мы можем упорядочить элементы множества A таким образом: a1, a2, a3, ... , an. Аналогично можем упорядочить элементы множества B: b1, b2, b3, ..., bm. Теперь мы хотим объединить эти два множества.
Чтобы объединить множества A и B, мы можем использовать следующую стратегию. Сначала возьмем первый элемент множества A, a1, затем первый элемент множества B, b1. Затем возьмем второй элемент множества A, a2, и второй элемент множества B, b2, и так далее. Мы переходим от элемента к элементу поочередно из двух множеств, и в итоге получаем последовательность a1, b1, a2, b2, a3, b3, ..., an, bn.
Цель исследования

Определение понятия "счетное множество"

Счетным множеством называется такое множество элементов, для которого существует взаимно однозначное соответствие каждого элемента множества с натуральным числом. Другими словами, счетное множество может быть упорядочено в последовательность, где каждому элементу множества соответствует некоторое натуральное число.
Натуральные числа, такие как 1, 2, 3 и так далее, являются примерами счетных множеств. Они образуют бесконечную последовательность, где каждое число имеет свой порядковый номер. Однако, счетные множества не ограничиваются только натуральными числами.
Примером счетного множества является множество всех целых чисел. Хотя множество целых чисел бесконечно, оно все равно может быть упорядочено в последовательность, где каждому целому числу соответствует натуральное число. Таким образом, множество целых чисел является счетным множеством.
Другим примером счетного множества является множество всех рациональных чисел. Рациональные числа представляют собой дроби, которые могут быть представлены в виде отношения двух целых чисел. Опять же, это множество бесконечно, но каждое рациональное число может быть упорядочено в последовательность, соответствующую натуральным числам.
| Примеры счетных множеств |
|---|
| Натуральные числа (1, 2, 3, ...) |
| Целые числа (...,-2,-1,0,1,2,...) |
| Рациональные числа (дроби) |
Счетность объединения двух счетных множеств
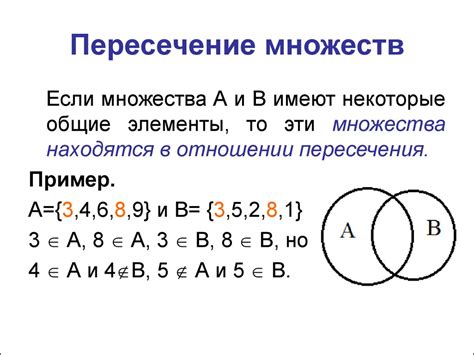
Для начала, допустим, что у нас есть два счетных множества A и B. По определению, счетное множество имеет биекцию с множеством натуральных чисел, то есть существует функция f: N -> A, которая отображает каждому натуральному числу в множество A без потерь информации.
Также, для множества B существует аналогичная функция g: N -> B.
Для доказательства счетности объединения A и B, мы можем построить новую функцию h: N -> A ∪ B следующим образом: для каждого нечетного числа n, h(n) = f((n+1)/2), а для каждого четного числа n, h(n) = g(n/2).
Таким образом, мы можем установить взаимно-однозначное соответствие между натуральными числами и элементами объединения A и B, что означает, что объединение двух счетных множеств также является счетным.
Данное доказательство основано на конструкции биекции между натуральными числами и элементами объединения A и B. Оно позволяет формально установить свойство счетности объединения двух счетных множеств и обобщает концепцию счетности на объединение множеств.
Примеры и применение
Доказательство счетности объединения двух счетных множеств применяется в различных областях математики и информатики. Вот несколько примеров, где это доказательство имеет значение:
1. Теория множеств: Доказательство счетности объединения двух счетных множеств позволяет понять и классифицировать бесконечные множества. Это полезно при изучении различных свойств и отношений между ними.
2. Теория графов: В графовой теории счетные множества используются для описания и анализа различных видов графов. Доказательство счетности объединения двух счетных множеств может быть полезным инструментом при исследовании графовых структур.
3. Криптография: В криптографии счетные множества часто используются для генерации случайных чисел или при шифровании информации. Доказательство счетности объединения двух счетных множеств может помочь в анализе и разработке криптографических алгоритмов.
4. Алгоритмы и структуры данных: Доказательство счетности объединения двух счетных множеств может быть полезным при разработке и анализе алгоритмов и структур данных. Оно может помочь в оптимизации работы программ и улучшении производительности.
В целом, доказательство счетности объединения двух счетных множеств имеет широкое применение в математике, информатике и других науках. Оно позволяет лучше понять и описать бесконечные множества, а также использовать их в различных вычислительных и алгоритмических задачах.



