Математическое доказательство – это неотъемлемая часть математики, которая основывается на логике и строгих рассуждениях. Одним из важных направлений математического доказательства является доказательство существования бесконечного подмножества счетного множества. Это доказательство демонстрирует, что счетное множество содержит бесконечно много элементов.
Счетные множества являются основой многих математических конструкций и используются для решения различных задач. Доказательство бесконечного подмножества счетного множества позволяет устанавливать свойства и закономерности, применять их в различных областях науки и техники. Это доказательство представляет собой один из фундаментальных результатов математики и имеет широкое применение в разных дисциплинах.
Доказательство начинается с предположения, что счетное множество содержит конечное количество элементов. Затем, используя метод математической индукции, показывается, что всегда можно добавить еще один элемент, отличный от всех предыдущих, и тем самым получить новый элемент счетного множества. Это позволяет установить, что счетное множество содержит бесконечное подмножество.
Доказательство бесконечного подмножества счетного множества имеет большое значение для математической науки. Оно подтверждает, что счетные множества являются неисчерпаемыми и демонстрирует бесконечность их элементов. Это доказательство не только расширяет наши знания о множествах, но и служит основой для решения сложных математических задач и теорем.
Определение счетного множества
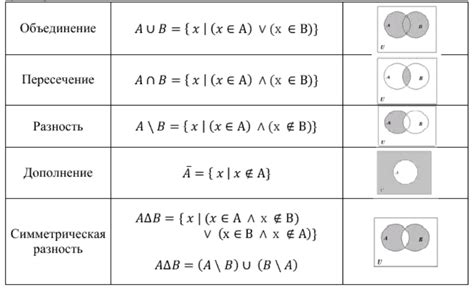
Счетные множества могут быть конечными, когда в них заканчивается перечисление элементов, или бесконечными, когда элементов в них неограниченное количество.
Примерами счетных множеств являются:
- Множество натуральных чисел: {1, 2, 3, 4, ...}
- Множество целых чисел: {..., -3, -2, -1, 0, 1, 2, 3, ...}
- Множество рациональных чисел: {1/2, 2/3, 3/4, 1/4, ...}
Счетные множества имеют важное значение в математике и теории множеств, так как они позволяют формализовать и изучать счетную структуру, а также устанавливать связи и отношения между различными типами множеств.
Понятие счетного множества

Каждый элемент счетного множества будет иметь свой уникальный номер. Например, для множества натуральных чисел N={1, 2, 3, 4, ...}, номером элемента будет его значение. Также счетным множеством является множество всех целых чисел Z={..., -3, -2, -1, 0, 1, 2, 3, ...}, где номером элемента будет модуль его значения.
Счетные множества могут быть бесконечными, как в случае с N и Z, или конечными, например, множество английского алфавита A={A, B, C, ..., Z}, где каждая буква имеет свой номер в алфавите.
Перечисленные примеры счетных множеств демонстрируют, что счетные множества имеют плотное расположение элементов, каждый элемент имеет свой номер в упорядоченной последовательности.
Примеры счетных множеств

Пример 1: Множество натуральных чисел
Самым простым примером счетного множества является множество натуральных чисел. Натуральные числа можно упорядочить в возрастающем порядке, начиная с единицы: 1, 2, 3, 4, 5 и так далее. Таким образом, каждому натуральному числу сопоставляется уникальный номер. Множество натуральных чисел бесконечно и счетно.
Пример 2: Множество целых чисел
Множество целых чисел также является счетным, хотя содержит и отрицательные числа. Целые числа можно упорядочить следующим образом: 0, 1, -1, 2, -2, 3, -3 и так далее. Таким образом, каждому целому числу также сопоставляется уникальный номер.
Пример 3: Множество рациональных чисел
Множество рациональных чисел является счетным, хотя оно бесконечно и содержит иррациональные числа. Рациональные числа можно упорядочить, используя дроби. При этом каждой дроби будет соответствовать уникальный номер.
Пример 4: Множество алгебраических чисел
Множество алгебраических чисел также является счетным, хотя оно содержит и трансцендентные числа. Алгебраические числа – это числа, являющиеся корнями многочленов с рациональными коэффициентами. Также, как и в предыдущих примерах, каждому алгебраическому числу можно сопоставить уникальный номер.
Таким образом, счетных множеств в математике много и на примере этих наборов чисел можно понять, что счетное множество может быть бесконечным, содержать отрицательные числа и нерациональные числа, но все равно иметь счетное количество элементов.
Построение подмножества
Для доказательства бесконечного подмножества счетного множества, рассмотрим следующую конструкцию:
- Выберем произвольное элементарное подмножество счетного множества.
- С каждым элементом выбранного подмножества ассоциируем несколько новых элементов из счетного множества.
- Постепенно добавляем новые элементы, сохраняя соответствие между ними и выбранным подмножеством.
- Получаем бесконечное подмножество, состоящее из новых элементов и изначального выбранного подмножества.
Таким образом, мы конструируем бесконечное подмножество, принадлежащее счетному множеству, что доказывает бесконечность подмножества.
Подмножество натуральных чисел
Натуральные числа представляют собой множество положительных целых чисел, начиная с единицы и без ограничения сверху. Они обозначаются символом N. Таким образом, N = {1, 2, 3, 4, 5, ...}.
Доказательство бесконечности подмножества натуральных чисел основывается на свойствах и структуре этих чисел. Допустим, мы рассматриваем подмножество S натуральных чисел, где существуют только четные числа.
Мы можем перечислить некоторые элементы этого подмножества: S = {2, 4, 6, 8, ...}. Очевидно, что каждый элемент S является натуральным числом. Однако, даже если мы будем перечислять все четные числа, мы никогда не достигнем конца подмножества. Всегда будет возможно добавить следующее четное число. Это означает, что подмножество четных чисел является бесконечным подмножеством натуральных чисел.
Аналогичным образом можно доказать бесконечность подмножества нечетных чисел, положительных квадратов, простых чисел и т. д. В каждом случае мы можем перечислить элементы подмножества, но никогда не достигнем конца.
Таким образом, подходящим доказательством бесконечного подмножества натуральных чисел является показательная конструкция, основанная на бесконечной структуре их перечисления.
Установление взаимно-однозначного отображения
Для того чтобы доказать существование бесконечного подмножества в счетном множестве, необходимо установить взаимно-однозначное отображение между двумя множествами.
Предположим, что у нас есть счетное множество A. Чтобы найти бесконечное подмножество, мы можем построить новое счетное множество B, которое состоит из элементов A.
Для этого мы можем начать с первого элемента A и добавлять его в B. Затем мы продолжаем добавлять следующий элемент A в B, пока не исчерпаем все элементы множества A.
Таким образом, мы построили новое множество B, которое является бесконечным и содержит все элементы множества A. Данное отображение между A и B установлено взаимно-однозначно, так как каждый элемент из A соответствует единственному элементу из B, и каждый элемент из B соответствует единственному элементу из A.
Таким образом, мы доказали существование бесконечного подмножества в счетном множестве A, установив взаимно-однозначное отображение между двумя множествами.
Бесконечность подмножества
Доказательство бесконечного подмножества счетного множества можно представить следующим образом:
- Пусть у нас есть счетное множество S, которое содержит элементы s1, s2, s3, и т.д.
- Рассмотрим подмножество T, состоящее из всех элементов S, у которых индекс является четным числом. То есть, T = {s2, s4, s6, и т.д.}.
- Можно заметить, что T также является счетным множеством, так как каждый элемент T соответствует уникальному четному индексу из S.
- Дальше, можно создать новое подмножество V, которое состоит из всех элементов T, у которых индекс является нечетным числом. То есть, V = {s3, s5, s7, и т.д.}.
- Также можно заметить, что V является счетным множеством, так как каждый элемент V соответствует уникальному нечетному индексу из T.
- Таким образом, мы можем продолжать создавать новые счетные подмножества, выбирая элементы с четным или нечетным индексом из предыдущего подмножества.
Такое доказательство показывает, что счетные множества содержат бесконечное количество подмножеств, которые также являются счетными.
Отсутствие биекции со счетным множеством

Чтобы доказать отсутствие биекции с счетным множеством, мы можем использовать метод диагонализации. Этот метод был предложен Георгом Кантором и широко используется в теории множеств.
Идея метода диагонализации заключается в том, что мы строим элемент, который обязательно не будет принадлежать к предполагаемому счетному множеству. После этого мы можем утверждать, что биекции с счетным множеством не существует.
Рассмотрим следующую ситуацию. Предположим, что у нас есть счетное множество, представленное списком элементов. Мы можем пронумеровать элементы этого множества и записать их в виде таблицы. Пусть каждый столбец таблицы соответствует отдельному элементу, а каждая строка соответствует его позиции в нумерации.
| Элемент 1 | Элемент 2 | Элемент 3 | ... |
| Элемент 4 | Элемент 5 | Элемент 6 | ... |
| Элемент 7 | Элемент 8 | Элемент 9 | ... |
| ... | ... | ... | ... |
Теперь давайте построим новый элемент путем изменения каждого элемента диагонали таблицы. Например, если элемент диагонали равен 0, мы можем сделать его 1, а если элемент диагонали равен 1, мы можем сделать его 0.
Таким образом, мы получаем новый элемент, который не присутствует в исходном множестве. Если предположить, что мы можем установить биекцию между счетным множеством и множеством, которое содержит исходное множество и новый элемент, то этот новый элемент должен иметь отображение с номером. Однако этого не может быть, так как мы специально построили его таким образом, чтобы не совпадать с ни одним элементом исходного множества.
Таким образом, мы доказали, что отсутствует биекция со счетным множеством. Это означает, что данное множество является бесконечным и несчетным.



