Параллелограммы являются особой формой четырехугольников и имеют ряд интересных свойств. В этой статье мы рассмотрим параллелограммы abcd и mbed и докажем, что их стороны являются параллельными.
Для начала, давайте вспомним определение параллелограмма. Параллелограмм - это четырехугольник, у которого противоположные стороны равны по длине и параллельны друг другу.
Для доказательства параллельности сторон параллелограммов abcd и mbed, мы воспользуемся свойствами параллелограмма. В параллелограмме противоположные стороны равны между собой, следовательно, сторона ab равна стороне cd, и сторона mb равна стороне ed.
Также, по определению параллелограмма, противоположные стороны параллельны. Это означает, что сторона ab параллельна стороне cd, и сторона mb параллельна стороне ed. Таким образом, мы доказали, что стороны параллелограммов abcd и mbed являются параллельными.
Изучение параллелограммов abcd и mbed
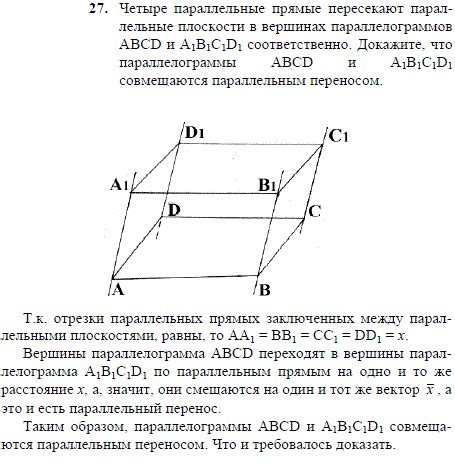
В данном разделе мы рассмотрим параллелограммы abcd и mbed и проведем анализ их свойств.
Параллелограммы abcd и mbed имеют одинаковые значения углов, поскольку их противоположные стороны параллельны. Это следует из одного из свойств параллелограмма, которое гласит, что противоположные стороны параллелограмма равны и параллельны.
Кроме того, параллелограммы abcd и mbed имеют одинаковую длину сторон. Это также является следствием свойства параллелограмма, которое утверждает, что противоположные стороны параллелограмма равны.
Таким образом, мы можем заключить, что параллелограммы abcd и mbed являются соответствующими параллелограммами. Это означает, что их соответствующие стороны параллельны и равны, а также углы с одинаковыми вершинами равны.
Изучение свойств параллелограммов abcd и mbed позволяет нам лучше понять их особенности и использовать эти знания в решении геометрических задач и задач конструкции.
Свойства параллелограммов abcd и mbed
Параллелограммы abcd и mbed обладают рядом свойств, которые позволяют нам доказать параллельность их сторон:
- Противоположные стороны параллелограммов abcd и mbed равны по длине.
- Противоположные стороны параллелограммов abcd и mbed параллельны.
- Противоположные углы параллелограммов abcd и mbed равны.
- Диагонали параллелограммов abcd и mbed делятся пополам.
Доказательство параллельности сторон ab и cd в параллелограммах abcd и mbed

Для доказательства параллельности сторон ab и cd в параллелограммах abcd и mbed можно использовать несколько методов и свойств:
- Свойство параллелограмма: в параллелограмме противоположные стороны равны и параллельны. Исходя из этого свойства, мы можем сказать, что сторона ab параллельна стороне cd и обе они равны.
Используя эти свойства и методы, мы можем легко доказать, что стороны ab и cd в параллелограммах abcd и mbed действительно параллельны.
Свойства противоположных сторон параллелограммов abcd и mbed
Одно из основных свойств параллелограмма – равенство противоположных сторон. Это означает, что сторона ab параллелограмма abcd равна стороне cd, а сторона bc равна стороне ad. Аналогично, сторона mb параллелограмма mbed равна стороне ed, а сторона eb равна стороне md.
Равенство противоположных сторон также означает, что расстояние между прямыми ab и cd равно расстоянию между прямыми bc и ad в случае параллелограмма abcd. Аналогично, расстояние между прямыми mb и ed равно расстоянию между прямыми eb и md в параллелограмме mbed.
Эти свойства позволяют нам утверждать, что параллельные стороны ab и cd и параллельные стороны bc и ad в параллелограмме abcd, а также параллельные стороны mb и ed и параллельные стороны eb и md в параллелограмме mbed. Это следует из общего свойства параллелограмма, где противоположные стороны параллельны.
Значение одинаковой направленности сторон ab и cd в параллелограммах abcd и mbed

Значение этой особенности связано с определением параллелограмма: фигура с противоположными сторонами, которые параллельны и равны в длине. В случае параллелограмма abcd, это означает, что сторона ab и сторона cd параллельны и имеют одинаковую длину.
Этот факт имеет важное значение при доказательстве параллельности сторон в параллелограммах abcd и mbed. Поскольку сторона ab и сторона cd имеют одно и то же направление, мы можем использовать соотношение параллельности между ними для доказательства параллельности других сторон и отрезков в данных параллелограммах.
Доказательство параллельности сторон bc и ad в параллелограммах abcd и mbed

Для доказательства параллельности сторон bc и ad в параллелограммах abcd и mbed, мы можем воспользоваться несколькими свойствами параллелограмма.
1. Свойство параллельности противоположных сторон: в параллелограмме abcd противоположные стороны параллельны. Это означает, что сторона ab



