Действительные числа a, b и c – это числа, которые могут быть представлены на числовой оси, то есть они могут принимать любое значение на вещественной прямой. Это важно учитывать при решении задач и проведении математических операций.
Действительные числа a, b и c могут иметь различные значения и свойства. Они могут быть положительными или отрицательными, рациональными или иррациональными. Важно учитывать эти свойства при выполнении различных математических операций и решении уравнений, чтобы получить правильный результат.
Что такое действительные числа?
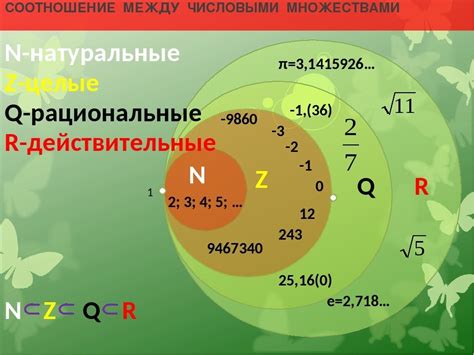
Рациональные числа представляют собой числа, которые могут быть выражены в виде дроби, где числитель и знаменатель являются целыми числами. Рациональные числа могут быть представлены как конечные десятичные дроби или периодические десятичные дроби.
Иррациональные числа представляют собой числа, которые не могут быть представлены в виде дроби. Они имеют бесконечное количество недвижущихся десятичных разрядов и не имеют периодической структуры. Иррациональные числа могут быть представлены в виде корня из неполного квадрата или как результат вычисления бесконечно длинного ряда.
Действительные числа образуют числовую прямую, которая представляет собой бесконечную прямую линию, где каждая точка соответствует определенному числу. Числа увеличиваются по мере движения в положительном направлении и уменьшаются по мере движения в отрицательном направлении.
Действительные числа играют важную роль в математике и науке, а также в повседневной жизни. Они используются для измерения, расчетов, моделирования и многих других приложений. Понимание и использование действительных чисел является неотъемлемой частью образования и общей математической грамотности.
Определение действительных чисел

Целые числа - это числа без десятичной части и без дробных значений. Они включают отрицательные числа, положительные числа и ноль.
Рациональные числа - это числа, которые могут быть представлены в виде дроби, где числитель и знаменатель являются целыми числами и знаменатель не равен нулю. Рациональные числа могут быть конечными или периодическими десятичными дробями.
Иррациональные числа - это числа, которые не могут быть представлены в виде дроби. Они имеют бесконечное количество десятичных знаков и не повторяются. Примерами иррациональных чисел являются корень квадратный из 2 и число пи (π).
Действительные числа включают и рациональные, и иррациональные числа, что делает их обширным множеством чисел, которые могут использоваться для моделирования и измерения различных физических явлений и математических задач.
Изучение действительных чисел и их свойств является важной частью математики и науки в целом, поскольку они встречаются повсюду в нашей повседневной жизни и широко используются для решения проблем и задач в различных областях.
Особенности действительных чисел
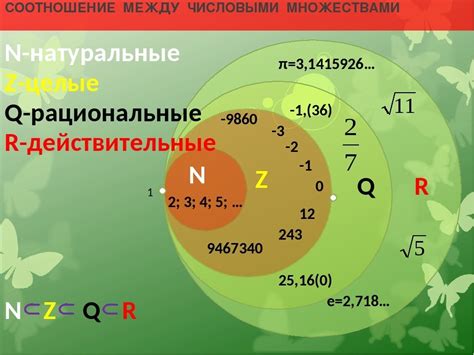
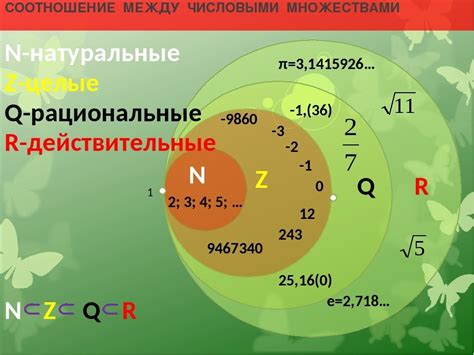
Одной из особенностей действительных чисел является их бесконечность. В отличие от натуральных чисел, которые начинаются с нуля и увеличиваются на единицу, или целых чисел, которые включают в себя отрицательные значения, действительные числа охватывают все возможные значения на числовой оси.
Действительные числа могут быть как рациональными, так и иррациональными. Рациональные числа можно представить в виде обыкновенных дробей или конечных или периодических десятичных дробей, в то время как иррациональные числа не могут быть представлены в такой форме и имеют бесконечное число недлинных, непериодических десятичных знаков.
Действительные числа имеют важное значение в научных расчетах, физике, экономике и других областях, где требуется точное измерение и представление значений. Они позволяют нам моделировать физические явления и решать сложные задачи.
Использование действительных чисел также может быть связано с некоторыми проблемами, такими как округление ошибок и неопределенности. Это происходит из-за конечной точности вычислений и представления чисел на компьютере или в других средствах хранения данных.
Примеры действительных чисел
| Число | Описание |
|---|---|
| 0 | Ноль является действительным числом, которое находится в центре числовой прямой и разделяет положительные и отрицательные числа. |
| 3 | Тройка - положительное действительное число, которое расположено справа от нуля на числовой прямой. |
| -2.5 | Минус два с половиной - отрицательное действительное число, которое находится слева от нуля на числовой прямой. |
| π (пи) | Число пи является иррациональным действительным числом, которое представляет собой отношение длины окружности к ее диаметру. |
| √2 (квадратный корень из 2) | Квадратный корень из 2 является иррациональным действительным числом, которое представляет собой длину гипотенузы прямоугольного треугольника со сторонами 1. |
Эти примеры демонстрируют разнообразие действительных чисел, которые могут быть положительными, отрицательными, иррациональными или рациональными. Все они имеют важное значение в математике и в повседневной жизни.
Свойства действительных чисел

- Действительные числа включают в себя как рациональные (числа, представимые в виде дроби), так и иррациональные (числа, которые не могут быть представлены в виде дроби). Это позволяет представить любое вещественное число на числовой оси.
- Одно из важных свойств действительных чисел - это их плотность. Это означает, что между любыми двумя действительными числами всегда можно найти другое действительное число. Например, между числами 1 и 2 можно найти бесконечное количество других чисел, таких как 1.5, 1.9, 1.99 и т.д.
- Действительные числа обладают свойствами сложения, вычитания, умножения и деления. Они подчиняются основным арифметическим операциям и образуют поле.
- Действительные числа образуют упорядоченное множество. Это означает, что любые два числа можно сравнить между собой: одно число может быть больше, меньше или равно другому числу.
Свойства действительных чисел являются основными основами математики и широко применяются в различных областях науки, экономики, физики и техники. Они позволяют нам изучать и описывать мир вокруг нас с использованием точных и логических методов.
Операции с действительными числами

Операции с действительными числами включают:
- Сложение: для сложения двух действительных чисел нужно сложить их целые и дробные части отдельно. Например, если имеются числа 2.3 и 1.8, то результат сложения будет 4.1.
- Вычитание: для вычитания одного действительного числа из другого нужно вычесть их целые и дробные части отдельно. Например, если имеются числа 5.7 и 3.2, то результат вычитания будет 2.5.
- Умножение: для умножения двух действительных чисел нужно умножить их целые и дробные части отдельно и сложить полученные произведения. Например, если имеются числа 2.5 и 1.2, то результат умножения будет 3.
- Деление: для деления одного действительного числа на другое нужно разделить их целые и дробные части отдельно. Например, если имеются числа 7.8 и 2.4, то результат деления будет 3.25.
Операции с действительными числами позволяют выполнять различные математические вычисления, как в повседневной жизни, так и в научных и технических расчётах.
Практическое применение действительных чисел

Один из основных сценариев использования действительных чисел – вычисления и измерения в научных и инженерных расчетах. Действительные числа позволяют точно представлять и оперировать с неограниченным диапазоном числовых значений. Например, в физике они позволяют моделировать и анализировать сложные физические процессы, такие как движение тел, электромагнитные поля, теплообмен и т.д.
Действительные числа также находят свое применение в экономике и финансах. Они позволяют проводить анализ и оценку финансовых данных, таких как расчеты доходности инвестиций, оценка стоимости активов и их изменений во времени, моделирование финансовых рынков и т.д. Действительные числа позволяют точно представлять и оперировать с величинами, имеющими десятичные доли и различные интервалы значений.
Еще одним практическим применением действительных чисел является статистический анализ и моделирование. Действительные числа применяются для оценки и предсказания различных параметров и вероятностей, таких как среднее значение, дисперсия, корреляция и многое другое. Они позволяют проводить различные виды статистических тестов и исследований с точностью до десятичных долей.
В повседневной жизни мы также сталкиваемся с практическим применением действительных чисел, примерами которых могут быть вычисления бюджета, расчеты стоимости товаров и услуг, конвертация валют, оценка времени и расстояний и т.д. Действительные числа позволяют нам точно и удобно оперировать с точными числовыми значениями в различных практических ситуациях.



