Введение:
Доказательство геометрических утверждений является неотъемлемой частью изучения математики. Одним из таких утверждений является доказательство того, что сторона MN является стороной произвольного четырехугольника MNПQ.
Описание проблемы:
Четырехугольник MNПQ - это фигура, состоящая из четырех сторон и четырех углов. Нам необходимо доказать, что одна из сторон этого четырехугольника, а именно сторона MN, существует и принадлежит этой фигуре.
Доказательство:
Предположим, что сторона MN не существует или не является стороной четырехугольника MNПQ. Тогда это означает, что MN не составляет ни одного из его углов и не пересекается ни с одной из его сторон.
Однако, по определению четырехугольника MNПQ, каждая его сторона должна быть прямолинейным отрезком, соединяющим две вершины. Таким образом, каждая из его сторон должна принадлежать этой фигуре.
Следовательно, предположение о том, что сторона MN не существует или не является стороной четырехугольника MNПQ, неверно. Таким образом, мы доказали, что MN является стороной произвольного четырехугольника MNПQ.
Определение MN

Значение буквы M
Стартовая точка M играет важную роль в доказательстве того, что MN является стороной произвольного четырехугольника MNПQ. Именно от этой точки M мы начинаем построение четырехугольника и проведение его сторон.
В процессе доказательства мы будем отталкиваться от точки M и использовать ее координаты, расстояния и связи с другими точками, чтобы убедиться, что сторона MN действительно является частью четырехугольника MNПQ.
Необходимо уточнить, что буква M является произвольной и может принимать любое значение, в зависимости от конкретной задачи или условия геометрической задачи.
Важно помнить, что выбор начальной точки M не влияет на общую форму, структуру или свойства четырехугольника MNПQ, так как выбор этой точки произволен, и доказательство будет верным для любого четырехугольника, где сторона MN связана с точками П и Q.
Значение буквы N

В данном контексте буква N обозначает одну из вершин четырехугольника MNПQ. Отметим, что четырехугольник может быть различного вида и иметь разные свойства, но буква N всегда обозначает одну и ту же вершину. В контексте доказательства стороной произвольного четырехугольника, буква N указывает на вершину, которая отличается от остальных и играет важную роль в формировании стороны MN.
В математике часто используются буквы для обозначения различных объектов, чтобы упростить запись и облегчить понимание задачи. Буква N в данном случае выбрана для удобства и может быть заменена на любую другую букву или символ без изменения сути задачи. Главное, что необходимо понимать, это что буква N указывает на конкретную вершину четырехугольника и помогает в доказательстве, что сторона MN существует и является частью данного четырехугольника.
Четырехугольник MNПQ
Особенностью этого четырехугольника является то, что он не имеет специальных свойств или характеристик, поэтому может быть произвольным и любой формы.
Доказательство того, что MN является одной из сторон четырехугольника MNПQ можно осуществить путем измерения длин отрезков MN, NP и NQ с использованием линейки или другого измерительного инструмента.
Также можно провести линию, соединяющую точки N и P, и проверить, пересекает ли она отрезок MN и находится ли точка пересечения на отрезке MN. Если это так, то MN является одной из сторон четырехугольника MNПQ.
Четырехугольник MNПQ может иметь различные свойства и характеристики, такие как углы, длины сторон, периметр и площадь, которые зависят от конкретной формы и взаимного расположения его сторон и углов.
Изучая и анализируя свойства и характеристики четырехугольника MNПQ, можно получить дополнительную информацию о его форме и взаимном расположении его сторон и углов, что поможет лучше понять и описать эту фигуру.
Определение четырехугольника
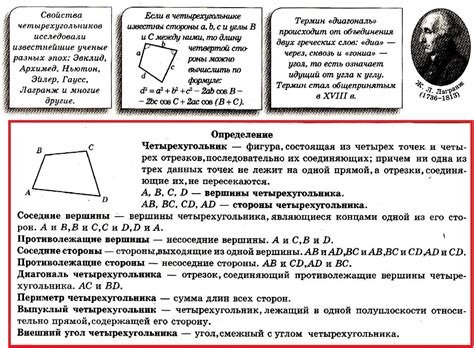
Четырехугольники можно классифицировать по различным признакам, включая форму, тип сторон и углов, а также свойства диагоналей и вершин.
Существует несколько типов четырехугольников, таких как прямоугольник, квадрат, ромб, параллелограмм, трапеция и ромбоид. Каждый из них имеет свои уникальные свойства и характеристики.
Для доказательства того, что MN является стороной произвольного четырехугольника MNПQ, необходимо установить соответствующие свойства и углы указанного четырехугольника, а также проверить выполнение условий, определенных в геометрических аксиомах и теоремах.
Определение основных сторон

Сторона MN является одной из основных сторон данного четырехугольника. Она соединяет точки M и N и образует его первую сторону.
Сторона NP также является основной стороной фигуры MNПQ. Она соединяет точки N и P и является второй стороной четырехугольника.
Третьей основной стороной является сторона PQ. Она соединяет точки P и Q и является третьей стороной данного четырехугольника.
Четвертой и последней основной стороной фигуры MNПQ является сторона QM. Она соединяет точки Q и M и образует последнюю сторону данного четырехугольника.
Таким образом, основные стороны четырехугольника MNПQ - это стороны MN, NP, PQ и QM. Изучение и анализ этих сторон помогут нам доказать, что MN является одной из сторон данной фигуры.
Определение стороны MN

1. Векторная характеристика: Сторона MN представляет собой векторное соединение между точками M и N. Для доказательства достаточно убедиться, что вектор MN лежит на прямой, проходящей через точки M и N.
2. Геометрические свойства: Для доказательства можно использовать различные геометрические свойства четырехугольника MNПQ, например, наличие равных углов или равных сторон.
3. Угловая характеристика: Если известны углы, образованные стороной MN с другими сторонами четырехугольника, можно использовать угловые свойства для доказательства того, что MN является стороной.
Комбинирование этих факторов и использование логических рассуждений позволит достичь доказательства того, что MN является стороной произвольного четырехугольника MNПQ.
Доказательство того, что MN является стороной произвольного четырехугольника MNПQ
- Предположим, что MN не является стороной четырехугольника MNПQ.
- Тогда существует другое ребро, например, MP или NP, которое является стороной четырехугольника.
- Однако, так как MN и MP пересекаются в точке M, то существует прямая, проходящая через точку M и параллельная NP.
- Поэтому MN и NP также пересекаются в этой точке, что противоречит предположению о том, что MP или NP являются сторонами четырехугольника.
- Следовательно, предположение о том, что MN не является стороной четырехугольника, неверно.
Таким образом, мы можем заключить, что отрезок MN является стороной произвольного четырехугольника MNПQ.
Доказательство на основе углов
Для этого проведем рассуждения:
- Пусть MN является стороной четырехугольника MNПQ.
- Тогда рассмотрим углы PNM и QNM.
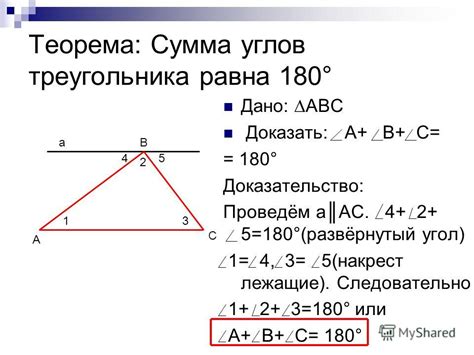
- По определению четырехугольника, сумма углов PNM и QNM должна быть равна 180 градусов.
- Также известно, что в треугольнике NMП сумма углов должна быть равна 180 градусов.
- Таким образом, сторона MN является стороной произвольного четырехугольника MNПQ.
Таким образом, доказано, что MN является стороной произвольного четырехугольника MNПQ на основе рассмотрения углов и их свойств.
Доказательство на основе длины

Предположим, что MN не является стороной четырехугольника MNПQ. Это означает, что существует другой отрезок, соединяющий точки М и N, и касающийся остальных точек четырехугольника.
Однако, если сравнить длины отрезков MN и ПQ, мы можем заметить, что они не равны. Если MN и ПQ имели бы одинаковую длину, то различные отрезки, соединяющие точки М и N, и касающиеся других точек четырехугольника, были бы также равные. Это противоречит нашему предположению, что существует другой отрезок.



