Четырехугольник - это геометрическая фигура, которая состоит из четырех сторон и четырех углов. Одним из интересных четырехугольников является фигура, у которой условие mb = de, где m и n - середины противолежащих сторон, a, b, c и d - длины сторон. Это условие связывает длины сторон четырехугольника и его диагоналей, и влияет на его свойства и особенности.
Одно из основных свойств четырехугольника с условием mb = de - это то, что он является равнобедренным. Это означает, что две стороны данной фигуры равны между собой. Благодаря равнобедренности, данный четырехугольник обладает некоторыми интересными свойствами, например, симметрией относительно оси симметрии, проходящей через середины противолежащих сторон.
Кроме того, четырехугольник с условием mb = de обладает так называемым космическим свойством. Это означает, что диагонали данной фигуры пересекаются в единственной точке, называемой средней точкой. Средняя точка - это точка пересечения диагоналей, которая делит их пополам. Благодаря этому свойству, данный четырехугольник имеет центральную симметрию относительно средней точки.
Четырехугольник с условием mb = de является интригующим объектом изучения в геометрии. Его свойства и особенности делают его интересным для учеников и ученых, позволяя изучать различные аспекты геометрии и применять их в практических задачах. Изучение данного четырехугольника помогает развивать навыки анализа, логического мышления и пространственного воображения.
Определение четырехугольника с условием mb = de: особенности и свойства
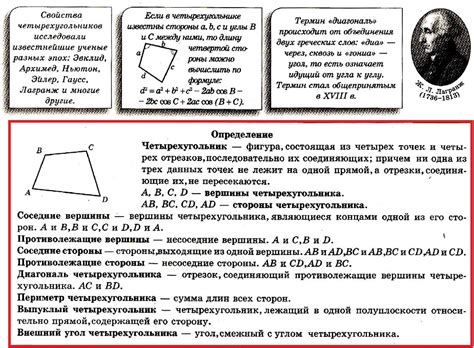
Особенностью четырехугольника с условием mb = de является равенство указанных расстояний. Это свойство позволяет рассматривать четырехугольник с условием mb = de как основу для решения различных геометрических задач и конструкций.
Одним из свойств четырехугольника с условием mb = de является равенство диагоналей, проходящих через середины противоположных сторон. Также данное условие позволяет установить равенство определенных углов внутри четырехугольника.
Важно отметить, что в случае, когда все стороны четырехугольника имеют одинаковую длину, данный четырехугольник с условием mb = de является прямоугольником.
Таким образом, четырехугольник с условием mb = de обладает рядом особенностей и свойств, которые делают его объектом изучения и применения в различных геометрических задачах.
Что такое четырехугольник с условием mb = de?
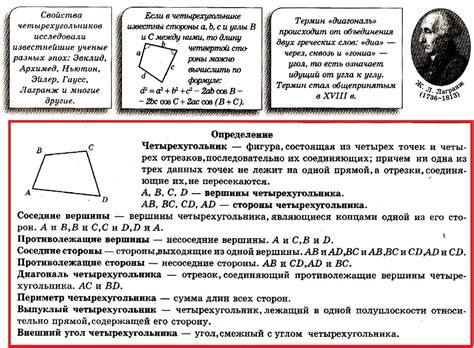
Условие mb = de является одним из свойств четырехугольника с условием mb = de. Другие важные свойства такого четырехугольника включают:
- Равенство длин других пар диагоналей: ma = cd и mc = ad.
- Совпадение точек пересечения медиан и точек пересечения диагоналей. Точка пересечения медиан называется центром масс четырехугольника.
- Симметричность относительно центра масс.
- Сумма длин противоположных сторон равна.
Четырехугольник с условием mb = de часто используется в геометрии для решения различных задач и построения различных фигур. Его свойства и особенности делают его полезным инструментом в анализе и изучении геометрических объектов.
| Свойства | Описание |
|---|---|
| mb = de | Равенство длин диагоналей |
| ma = cd и mc = ad | Равенство длин других пар диагоналей |
| Центр масс | Точка пересечения медиан и диагоналей |
| Симметричность | Относительно центра масс |
| Сумма длин противоположных сторон | Равна |
Характеристики четырехугольника с условием mb = de

Четырехугольник, в котором длины сторон mb и de равны, обладает несколькими особенностями и характеристиками.
| Свойство | Описание |
|---|---|
| Стороны | Четырехугольник с условием mb = de имеет четыре стороны, обозначенные как ab, bc, cd и da. Сторона mb равна стороне de. |
| Углы | Углы в этом четырехугольнике обозначены как углы A, B, C и D. Угол A соответствует точке a, угол B - точке b, угол C - точке c, а угол D - точке d. |
| Диагонали | Диагонали этого четырехугольника вычисляются как отрезки, соединяющие противоположные вершины. В данном случае, диагональ bd равна диагонали ce. |
| Периметр | Периметр четырехугольника с условием mb = de рассчитывается как сумма длин всех его сторон. Обозначим его как P. Тогда P = ab + bc + cd + da |
| Площадь | Площадь этого четырехугольника можно вычислить различными способами, в зависимости от известных данных. Например, если мы знаем длины сторон и угол между ними, то можно использовать формулу для расчета площади треугольника или применить формулу Герона для расчета площади четырехугольника. |
| Специальные случаи | Если длины сторон и углы в четырехугольнике с условием mb = de обладают определенными соотношениями, то он может быть классифицирован, например, как квадрат, прямоугольник или ромб. |
Четырехугольник с условием mb = de представляет собой интересный объект для изучения и анализа в геометрии. Его свойства и особенности могут помочь в решении различных задач и построении различных конструкций.
Как определить четырехугольник с условием mb = de?
Чтобы определить, является ли четырехугольник с условием mb = de, нужно проверить выполнение следующих условий:
- Строим отрезки mb и de.
- Измеряем длины отрезков mb и de.
- Сравниваем полученные значения длин.
Если длины отрезков mb и de равны, то четырехугольник удовлетворяет условию mb = de и является параллелограммом.
Важно отметить, что параллелограмм может иметь и другие свойства, например, равные углы между сторонами или диагонали. Поэтому, при анализе свойств четырехугольника с условием mb = de следует учитывать и другие характеристики фигуры.
Основные свойства четырехугольника с условием mb = de

1. Равные стороны:
В четырехугольнике с условием mb = de все стороны имеют равную длину. Это значит, что сторона mb и сторона de имеют одинаковую длину.
2. Равные углы:
Углы mb и de в таком четырехугольнике также равны между собой. Это свойство называется равенством вертикальных углов.
3. Равенство диагоналей:
Диагонали четырехугольника с условием mb = de имеют одинаковую длину. Это можно доказать, используя свойство равных сторон и равных углов.
4. Существование центра вписанной окружности:
В четырехугольнике с условием mb = de можно вписать окружность. Ее центр будет находиться точно в середине между диагоналями mb и de.
5. Условие равнобедренности:
В условиях mb = de можно сказать, что четырехугольник является равнобедренным. Это значит, что пары сторон, образованных между сторонами mb и de, будут равны между собой.
Как провести диагонали четырехугольника с условием mb = de?
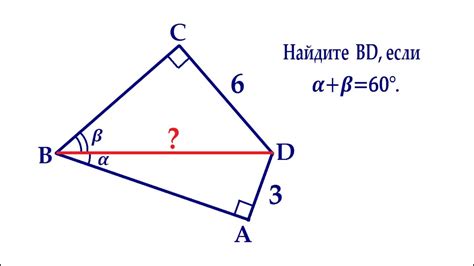
Для проведения диагоналей в таком четырехугольнике с условием mb = de следует использовать следующие шаги:
- Найдите середины сторон mb и de, обозначим их как M и D соответственно.
- Проведите отрезок MD. Этот отрезок будет являться одной из диагоналей исходного четырехугольника.
- Найдите середины сторон me и bd, обозначим их как L и K соответственно.
- Проведите отрезок LK. Этот отрезок будет являться второй диагональю четырехугольника.
По свойствам четырехугольника, стороны, соединяющие середины противоположных сторон, являются диагоналями, которые делятся пополам. Таким образом, длины md и lk равны половине длин исходных сторон mb и de соответственно.
В результате проведенных диагоналей в четырехугольнике с условием mb = de получается две диагонали, разделяющие четырехугольник на четыре треугольника.
Следует отметить, что данное свойство применимо только для четырехугольников, удовлетворяющих условию mb = de. Для шестиугольников, восьмиугольников и других многоугольников это свойство может не выполняться.
Определение перпендикулярности сторон в четырехугольнике с условием mb = de
Таким образом, если стороны mb и de в четырехугольнике с условием mb = de являются равными, то они также будут перпендикулярными друг другу.
Примеры применения четырехугольников с условием mb = de в задачах геометрии
1. Построение треугольника по заданным сторонам.
Если нам даны три стороны треугольника (a, b и c), то мы можем использовать четырехугольник с условием mb = de для определения четвертой стороны треугольника. Для этого нужно взять сторону b и провести линию, соединяющую точку m с точкой e. Получим четырехугольник mbde, в котором стороны mb и de будут равны по условию. Затем, можно построить перпендикуляр из точки b к отрезку de, чтобы определить точку h, и тем самым определить четвертую сторону треугольника.
2. Определение дополнительного угла в треугольнике.
Пусть в треугольнике abc заданы углы a и b. Чтобы найти угол c, можно использовать четырехугольник с условием mb = de. Для этого проводим линии, соединяющие точку m с точкой e, и получаем четырехугольник mbde. Затем, находим угол между сторонами mb и de, который будет равен углу c в треугольнике abc.
3. Решение задач на подобие треугольников.
При решении задач на подобие треугольников можно использовать четырехугольники с условием mb = de для нахождения неизвестных сторон или углов. При нахождении подобных треугольников, мы можем использовать свойства четырехугольника mbde для получения дополнительной информации об углах и сторонах.
Таким образом, четырехугольник с условием mb = de имеет широкий диапазон применений в задачах геометрии, помогая нам находить неизвестные стороны, углы и решать задачи на подобие треугольников.
Что делать, если условие mb = de не выполняется?

- Проверьте корректность измерений сторон и диагоналей: перепроверьте заданные значения и убедитесь, что они правильно указаны.
- Проверьте корректность построения фигуры: убедитесь, что стороны и диагонали правильно соединены. Проверьте, что углы согласованы и сумма длин сторон фигуры соответствует измеренным значениям.
- Обратитесь к геометрическим свойствам четырехугольников: убедитесь, что в фигуре выполнены все необходимые условия для того, чтобы она считалась четырехугольником. Например, проверьте, что сумма углов фигуры равна 360 градусов.
- Попробуйте использовать другие методы проверки фигуры: если текущий метод не дает правильного результата, можно попробовать другие методы, например, использовать теорему Пифагора или теорему косинусов для проверки соотношения между сторонами и диагоналями.
Если ни одно из вышеперечисленных действий не приводит к правильному результату, возможно, фигура не является четырехугольником или условие mb = de неприменимо в данном случае. В такой ситуации следует обратиться к учителю или специалисту по геометрии для получения дальнейшей помощи и разъяснений.



