Прямая лежит в плоскости треугольника - это геометрическое условие, когда прямая полностью находится внутри плоскости, ограниченной треугольником. При этом прямая может пересекать одну или несколько сторон треугольника, но не должна выходить за его границы.
Исследование положения прямых в плоскости треугольника имеет большое значение в геометрии и находит применение в различных областях. Знание, когда прямая лежит в плоскости треугольника, позволяет определить, пересекает ли прямая треугольник, и находить точки пересечения прямых и сторон треугольника.
Для того чтобы определить, лежит ли прямая в плоскости треугольника, необходимо выполнить следующие условия:
- Прямая должна находиться в одной плоскости с треугольником;
- Прямая должна пересекать две или три стороны треугольника, но не должна выходить за его границы;
- Прямая не должна совпадать с одной из сторон треугольника или быть параллельной ей.
Обращаясь к геометрии, анализируя положение прямой и треугольника на плоскости, можно получить информацию о геометрических свойствах фигур и решить задачи с использованием геометрических методов. Знание условий, когда прямая лежит в плоскости треугольника, откроет перед нами широкие возможности в решении геометрических задач.
Что значит, что прямая лежит в плоскости треугольника
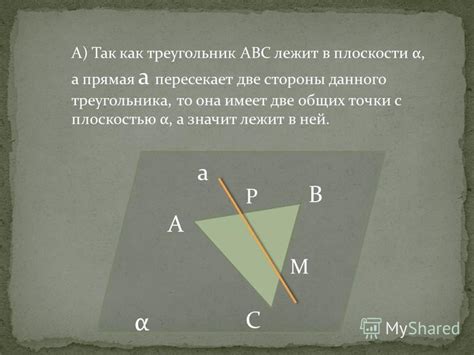
Когда говорят, что прямая лежит в плоскости треугольника, это означает, что прямая полностью находится в одной плоскости вместе с треугольником. То есть, все точки прямой можно представить как точки, принадлежащие этой плоскости, в которой также лежит треугольник.
Если прямая пересекает хотя бы одну сторону треугольника, то она уже не лежит в самом треугольнике и не считается лежащей в его плоскости.
Определить, лежит ли прямая в плоскости треугольника, можно с помощью геометрических методов. Например, можно провести параллельные прямые к сторонам треугольника и проверить, пересекает ли их исследуемая прямая. Если пересечение происходит, то прямая не лежит в плоскости треугольника, в противном случае - лежит.
Идея плоскости в геометрии
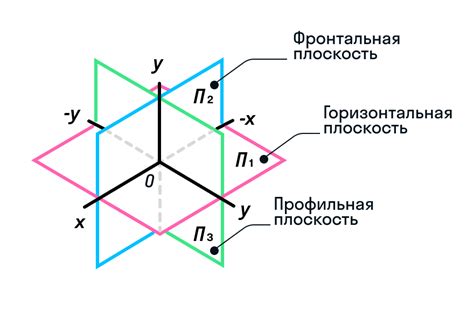
Плоскость АВС может быть определена через три точки, которые не лежат на одной прямой. Любые две линии в пространстве могут существовать в одной плоскости или в разных плоскостях. Однако, интерес представляют случаи, когда прямая целиком лежит в плоскости треугольника.
Прямая, лежащая в плоскости треугольника, означает, что все точки этой прямой лежат на плоскости, проходящей через вершины треугольника и содержащей все его стороны.
Треугольник как базовая фигура
В геометрии часто используется понятие прямой, которая является бесконечным набором точек, расположенных на одной линии. Прямая может проходить через вершины треугольника или лежать внутри его сторон. Если прямая проходит через одну из сторон треугольника, то она называется стороной треугольника. Если же прямая лежит внутри треугольника и не принадлежит ни одной из его сторон, то она говорит о том, что прямая лежит в плоскости треугольника.
Прямая, лежащая в плоскости треугольника, может иметь различные положения относительно этой плоскости. Например, прямая может пересекать все три стороны треугольника и быть отличной от любой из них. В таком случае, она называется пересекающей прямой. Также прямая может проходить через одну из сторон треугольника или быть параллельной одной из сторон. Или она может лежать внутри треугольника, но не пересекать его сторон.
Изучение прямых, лежащих в плоскости треугольника, позволяет углубить понимание его формы и особенностей. Умение определять и анализировать положение прямых внутри треугольника является важной навыком при решении геометрических задач и задач по построению треугольников.
Сущность прямой линии

Главная особенность прямой линии заключается в том, что она всегда лежит в одной плоскости. Плоскость - это геометрическое пространство, не имеющее толщины, но расширяющееся в двух измерениях - длине и ширине. Таким образом, прямая линия может быть представлена как граница плоскости или как отрезок, лежащий на этой плоскости.
В контексте треугольника прямая линия считается лежащей в плоскости треугольника, если она проходит через две или более его вершин. Такая линия может быть отрезком, диагональю или боковой стороной треугольника. Прямая линия, проходящая через все три вершины треугольника, называется медианой.
Изучение прямых линий и их взаимодействия с плоскостью является одним из основных аспектов геометрии. Понимание сущности прямой линии и ее связи с плоскостью треугольника позволяет анализировать и решать различные геометрические задачи, а также строить более сложные фигуры и объекты.
Выражение лежания прямой в плоскости треугольника
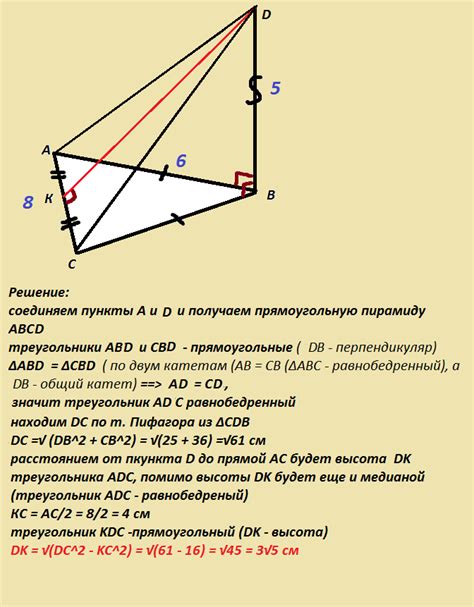
Лежание прямой в плоскости треугольника означает, что все точки этой прямой принадлежат данной плоскости и могут быть представлены как пересечение прямой с этой плоскостью. В геометрическом плане, прямая, лежащая в плоскости треугольника, не пересекает никакую его сторону и не выходит за пределы треугольника.
Выражение лежания прямой в плоскости треугольника можно также представить в виде уравнения. Если уравнение прямой, заданное в координатной системе, удовлетворяет уравнению плоскости, заданному треугольником, то прямая лежит в плоскости треугольника.
Выражение лежания прямой в плоскости треугольника является важным понятием в геометрии. Это позволяет определить, как прямые и треугольники взаимодействуют между собой, а также решать различные задачи, связанные с треугольниками и их сторонами.
Определение плоскости треугольника
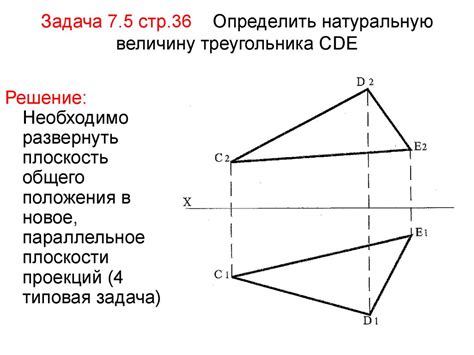
Для определения плоскости треугольника необходимо знать координаты трех его вершин, которые обозначаются точками A, B и C. Плоскость треугольника можно представить в виде алгебраического уравнения, которое выражается отношениями между координатами вершин и их компонентами. В общем случае, уравнение плоскости треугольника имеет вид Ax + By +Cz + D = 0, где A, B и C - коэффициенты уравнения, а D - свободный член.
Если треугольник лежит в плоскости, это означает, что его все три вершины А, В и С принадлежат одной плоскости и могут быть представлены с помощью заданного уравнения плоскости. Поэтому, для проверки того, что прямая лежит в плоскости треугольника можно использовать уравнение плоскости и проверить, удовлетворяют ли координаты точек прямой это уравнение.
Как определить, что прямая лежит в плоскости треугольника
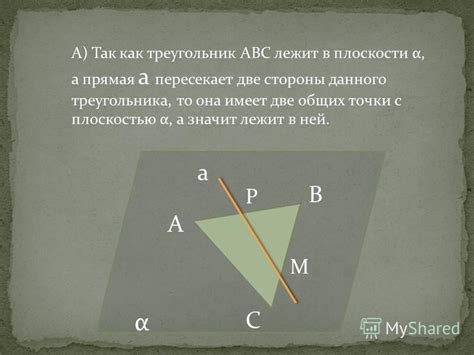
Чтобы определить, лежит ли прямая в плоскости треугольника, мы можем использовать несколько методов и критериев.
- Метод пересечения: Если прямая пересекает все стороны треугольника, то она лежит в его плоскости.
- Метод проекции: Если все точки прямой могут быть представлены в виде линейной комбинации точек треугольника, то прямая лежит в его плоскости.
- Метод векторного произведения: Если векторное произведение любой стороны треугольника и вектора, задающего прямую, равно нулю, то прямая лежит в его плоскости.
Также важно учитывать особые случаи:
- Если треугольник вырожденный (имеет нулевую площадь), то любая прямая, проходящая через его вершины, будет лежать в его плоскости.
- Если прямая параллельна одной из сторон треугольника, то она лежит в его плоскости.
В общем случае, чтобы определить, лежит ли прямая в плоскости треугольника, необходимо рассмотреть все описанные выше методы и критерии, основываясь на геометрических свойствах и условиях задачи.
Свойства прямой линии в плоскости треугольника
Прямая линия, лежащая в плоскости треугольника, обладает несколькими интересными свойствами:
1. Пересечение с сторонами треугольника:
Если прямая линия лежит в плоскости треугольника, она может пересекать его стороны в точках, лежащих как внутри треугольника, так и на его границе.
Если точка пересечения находится внутри треугольника, то можно сказать, что прямая делит треугольник на две части. Если точка пересечения находится на границе треугольника, то прямая лежит на одной из его сторон.
2. Параллельность:
Если прямая линия лежит в плоскости треугольника и параллельна одной из его сторон, то она будет параллельна всем его сторонам. Параллельность прямой с одной стороной треугольника означает, что она никогда не пересечет эту сторону и будет лежать на равном расстоянии от нее.
3. Прямая линия как медиана или высота:
Если прямая линия лежит в плоскости треугольника и проходит через его вершину, то она может быть медианой или высотой треугольника.
Медиана - это линия, проведенная из вершины треугольника к середине противоположной стороны. Прямая, соединяющая вершину треугольника и середину противоположной стороны, называется медианой. Если прямая линия является медианой, то она делит стороны треугольника пополам.
Высота треугольника - это прямая линия, опущенная из вершины треугольника к основанию, перпендикулярная стороне или ее продолжению. Если прямая линия является высотой треугольника, то она будет перпендикулярна стороне и проходить через ее середину.
Используя эти свойства прямой линии в плоскости треугольника, можно проводить различные геометрические рассуждения и решать задачи, связанные с треугольниками.
Практическое применение понятия лежания прямой в плоскости треугольника
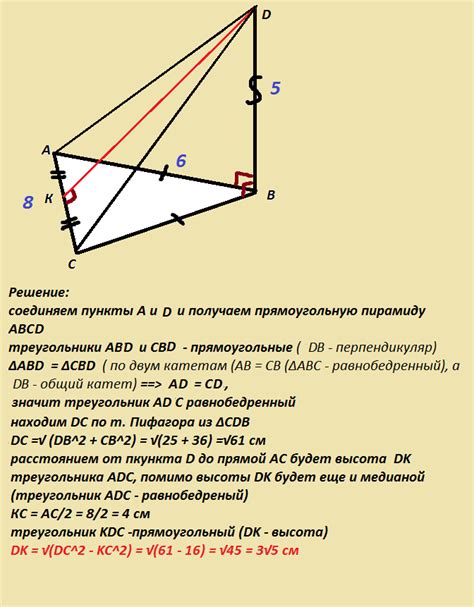
Понятие "прямая лежит в плоскости треугольника" имеет множество практических применений в различных областях. Рассмотрим некоторые из них:
- Геометрия. Понимание, что прямая лежит в плоскости треугольника, позволяет выполнять различные геометрические конструкции, такие как построение высот, биссектрис и медиан треугольника. Это важно для решения задач по геометрии и анализу треугольников.
- Графика. В компьютерной графике применяются алгоритмы и методы, основанные на понятии лежания прямой в плоскости треугольника. Например, алгоритм заполнения треугольника цветом (triangle rasterization) использует данное понятие для определения точек, входящих внутрь треугольника и подлежащих закрашиванию.
- Компьютерное зрение. В области компьютерного зрения требуется определение положения прямых в плоскости треугольника для решения различных задач. Например, определение положения ребер трехмерных объектов относительно проекции на изображение или определение столкновений объектов.
- Конструкционное моделирование. Понимание, что прямая лежит в плоскости треугольника, важно при создании трехмерных моделей и их анализе. Например, при создании трехмерного меша множество прямых лежат в плоскости треугольника, и их учет позволяет корректно определить свойства и поведение модели.
Когда говорят, что прямая лежит в плоскости треугольника, это означает, что все точки этой прямой находятся в той же плоскости, в которой лежит треугольник.
Если прямая полностью лежит внутри треугольника, то она пересекает все его стороны и вершины. Это означает, что все точки этой прямой находится внутри треугольника и не выходят за его границы.
Если прямая лежит на одной из сторон треугольника, то она касается этой стороны в одной или двух точках. В этом случае прямая лежит в плоскости треугольника, но некоторые ее точки могут находиться за его границей.
Если прямая пересекает одну или несколько сторон треугольника, то она лежит в плоскости треугольника, но не все ее точки находятся внутри треугольника. Некоторые точки прямой будут находиться вне треугольника.



