Позиционная система счисления – одна из основных математических систем, которая используется для записи и представления чисел. В отличие от других систем, таких как римская или двоичная, позиционная система основана на позиции цифры в числе, что делает ее универсальной и удобной для использования.
В позиционной системе счисления каждая позиция имеет свою весовую степень, которая зависит от основания системы. Например, в десятичной системе весовые степени увеличиваются в 10 раз с каждой следующей позицией: единицы, десятки, сотни и т.д. Таким образом, число 1234 в десятичной системе будет представлено как 1 тысяча, 2 сотни, 3 десятки и 4 единицы.
Однако, позиционная система счисления может иметь и другое основание. Например, в двоичной системе (основание 2) есть только две позиции: ноль и единица. Поэтому число 101 в двоичной системе будет представлено как 1 четыре, 0 двоек и 1 единица.
Что такое позиционная система счисления
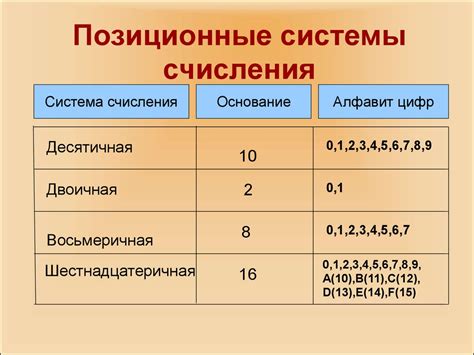
Основание системы счисления определяет количество различных символов, которые могут использоваться для представления чисел. Например, в десятичной системе счисления основанием является число 10, и для представления чисел используются 10 различных символов от 0 до 9.
В позиционной системе счисления каждая цифра в числе занимает определенную позицию, начиная с правой стороны. Значение цифры в позиции определяется умножением значения самой цифры на основание системы в степени позиции. Например, в десятичной системе число 3511 можно интерпретировать как 3 * 10^3 + 5 * 10^2 + 1 * 10^1 + 1 * 10^0.
| Цифра | Позиция | Значение |
|---|---|---|
| 3 | 3 | 3000 |
| 5 | 2 | 500 |
| 1 | 1 | 10 |
| 1 | 0 | 1 |
Позиционная система счисления используется во многих областях, включая математику, информатику и электронику. Она предоставляет удобный и эффективный способ представления и операций с числами.
Важность позиционной системы счисления
Универсальность: Позиционная система счисления позволяет представлять любое число с помощью ограниченного набора символов. Благодаря такому представлению, мы можем работать с числами разных порядков величины, от маленьких до огромных.
Удобство и простота использования: Позиционная система счисления основана на простом принципе разделения числа на разряды и использования ограниченного набора цифр. Это делает счет и выполнение арифметических операций над числами легкими и интуитивно понятными.
Широкое применение: Позиционная система счисления используется во многих областях, включая математику, физику, компьютерные науки, экономику и технику. Она является основой для работы с числами в компьютерах и программировании, а также необходима для анализа данных, проведения вычислений и решения различных задач.
Эффективность расчетов: Благодаря позиционной системе счисления мы можем выполнять различные арифметические операции, такие как сложение, вычитание, умножение и деление, с большой точностью и эффективностью. Это позволяет нам решать сложные математические задачи и проводить вычисления, которые раньше были невозможны.
Таким образом, позиционная система счисления является неотъемлемой частью нашей жизни и широко применяется в различных областях. Понимание ее принципов и основных преимуществ позволяет нам более эффективно работать с числами и проводить математические вычисления.
Принцип работы
Позиционная система счисления работает на основе принципа, что значение каждой цифры в числе зависит не только от самой цифры, но и от ее позиции в числе.
Для примера, возьмем десятичную систему счисления, которую мы используем в повседневной жизни. В десятичной системе есть десять цифр: от 0 до 9. Когда мы записываем число, каждая цифра имеет свою позицию, основанную на степени десятки. Например, число 256 имеет цифру 6 в позиции единиц, цифру 5 в позиции десятков и цифру 2 в позиции сотен.
Аналогично, в других позиционных системах счисления, таких как двоичная, восьмеричная или шестнадцатеричная, каждая цифра имеет свою позицию, которая зависит от степени основания системы счисления.
Примерно так же, как мы можем складывать и вычитать числа в десятичной системе, мы также можем выполнять арифметические операции в других позиционных системах счисления. Для этого мы применяем правила для сложения, вычитания, умножения и деления, основанные на основании системы счисления.
| База | Цифры | Пример |
|---|---|---|
| Десятичная | 0-9 | 256 |
| Двоичная | 0-1 | 11010000 |
| Восьмеричная | 0-7 | 740 |
| Шестнадцатеричная | 0-9, A-F | A3B |
Таблица показывает различные системы счисления, использующиеся на практике, и их соответствующие цифры.
Основные элементы системы счисления
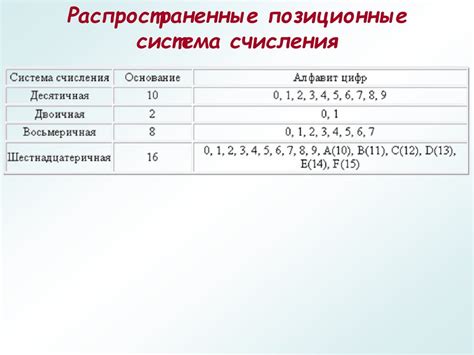
Основными элементами позиционной системы счисления являются:
1. База или основание системы счисления. Основание системы счисления определяет количество различных символов, которыми мы можем представлять числа. Например, в десятичной системе счисления (основание 10) мы используем 10 символов: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
2. Цифры. Цифры представляют собой используемые символы в системе счисления. Количество цифр определяется основанием системы счисления. В десятичной системе счисления цифры от 0 до 9. В двоичной системе счисления цифры только 0 и 1.
3. Позиции. Позиции в позиционной системе счисления определяют, какие степени основания надо использовать для расчета значения каждой цифры в числе. Например, в десятичной системе старшая позиция слева имеет вес 10^0, следующая - 10^1, затем 10^2 и так далее.
4. Знак. Знак указывает на то, является ли число положительным или отрицательным. Однако в позиционной системе счисления знак обычно не включается в само число, а используется отдельный символ или специальное правило для указания на знак числа.
5. Разряды. Разряды в позиционной системе счисления представляют собой отдельные позиции в числе. Каждая позиция в числе имеет определенный вес, определяющий вклад этой позиции в общее значение числа. Например, в десятичной системе счисления число 123 имеет три разряда: сотни, десятки и единицы.
6. Префиксы. Префиксы используются для обозначения основания системы счисления. Например, "0b" обозначает двоичную систему счисления, "0x" - шестнадцатеричную, "0o" - восьмеричную. Эти префиксы позволяют легко распознать основание системы счисления по представленному числу.
Взаимодействие всех этих элементов позволяет нам представлять различные числа в позиционной системе счисления и выполнять различные арифметические операции с ними.
Пример преобразования числа из одной системы счисления в другую

Для наглядности рассмотрим пример преобразования числа из десятичной системы счисления в двоичную.
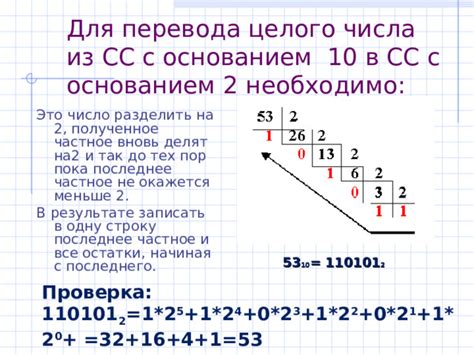
Пусть у нас есть число 42 в десятичной системе. Чтобы преобразовать его в двоичную систему, мы последовательно делим число на два и запоминаем остатки.
Процесс:
42 / 2 = 21, остаток 0
21 / 2 = 10, остаток 1
10 / 2 = 5, остаток 0
5 / 2 = 2, остаток 1
2 / 2 = 1, остаток 0
1 / 2 = 0, остаток 1
Чтобы получить двоичное представление числа, нужно записать остатки снизу вверх. В нашем случае это будет: 101010.
Таким образом, число 42 в десятичной системе счисления равно числу 101010 в двоичной системе.
Преимущества и недостатки

Преимущества позиционной системы счисления:
1. Универсальность: позиционная система счисления может быть использована для представления чисел любого размера, от небольших до очень больших.
2. Простота: основанные на позиционной системе счисления алгоритмы представления, сложения, вычитания и умножения чисел являются относительно простыми и понятными.
3. Эффективность: использование позиционной системы счисления позволяет эффективно использовать ресурсы памяти и вычислительной мощности.
4. Возможность представления дробных чисел: позиционная система счисления позволяет представлять десятичные дроби с высокой точностью.
Недостатки позиционной системы счисления:
1. Сложность чтения и записи чисел: в большинстве случаев требуется использование дополнительных символов (например, знаков плюс и минус) для представления чисел.
2. Ограниченная точность: из-за ограниченного количества символов, используемых в позиционной системе счисления, некоторые числа могут быть представлены только с ограниченной точностью.
3. Вычислительная сложность: выполнение сложных операций, таких как деление или извлечение квадратного корня, может быть сложно и требует дополнительных вычислительных ресурсов.
4. Неоднозначность символов: в некоторых случаях символы, используемые в позиционной системе счисления, могут быть неоднозначными и могут вызывать путаницу при чтении и записи чисел.
Преимущества позиционной системы счисления

Позиционная система счисления предоставляет ряд преимуществ, которые делают ее предпочтительной для использования в различных областях. Некоторые из наиболее значимых преимуществ:
| 1. | Универсальность: позиционная система счисления может быть использована для представления чисел в любой системе счисления, включая десятичную, двоичную, восьмеричную или шестнадцатеричную систему. |
| 2. | Простота использования: при работе с позиционной системой счисления нет необходимости запоминать отдельные символы или числа для каждой позиции. Вместо этого используются одни и те же символы и цифры для всех позиций. |
| 3. | Вычислительная эффективность: позиционная система позволяет выполнять различные арифметические операции, такие как сложение, вычитание, умножение и деление, с помощью простых правил, применимых к каждой позиции числа. |
| 4. | Гибкость: позиционная система счисления позволяет представлять числа любой длины, от маленьких до очень больших, без необходимости изменения самой системы счисления. |
| 5. | Поддержка различных математических операций: позиционная система счисления обеспечивает возможность проведения различных операций, таких как возведение в степень, извлечение корня и логарифмирование, используя те же правила, которые применяются к обычным арифметическим операциям. |
| 6. | Многообразие применений: позиционная система счисления широко используется в различных областях, включая математику, компьютерную науку, электронику, физику, информатику и даже в повседневной жизни. |
Все эти преимущества позволяют позиционной системе счисления оставаться оптимальным выбором при работе с числами в различных контекстах.
Недостатки позиционной системы счисления

Позиционная система счисления, несмотря на свою широкую применяемость и эффективность, также имеет некоторые недостатки.
- Сложность восприятия: Для людей, не знакомых с позиционной системой счисления, ее понимание может представлять определенные сложности. Необходимо усвоить концепцию разрядов и позиций, что может потребовать некоторого времени и усилий.
- Ошибки при записи и чтении чисел: В позиционной системе счисления несоблюдение правил записи чисел может приводить к ошибкам. Допущение опечаток или неправильное расположение цифр может существенно изменить значение числа.
- Неявное представление нуля: В позиционной системе счисления отсутствие цифр в разрядах считается нулевым значением. Однако это может вызывать путаницу при чтении чисел, особенно при работе с большими числами.
- Зависимость от базы системы: Изменение базы позиционной системы счисления может существенно влиять на запись и чтение чисел. При переходе от одной системы счисления к другой необходимо изменять разрядность чисел и применять другие правила записи.
Несмотря на эти недостатки, позиционная система счисления является удобным и мощным инструментом для работы с числами, используется во множестве областей и является основой для работы с компьютерами.
Применение в технологиях

Позиционная система счисления имеет широкое применение в различных технологиях. Ее основные области применения включают:
- Компьютерные сети: в сетевых протоколах часто используется двоичная система счисления, которая является позиционной системой.
- Криптография: позиционная система счисления используется в алгоритмах шифрования и дешифрования информации.
- Цифровая обработка сигналов: в области обработки аудио- и видеоданных также применяются позиционные системы счисления.
- Компьютерная графика: при работе с цветами и изображениями используются позиционные системы счисления, такие как RGB и CMYK.
- Арифметические операции: позиционная система счисления широко применяется в математических операциях, таких как сложение, вычитание, умножение и деление.
- Программирование и разработка ПО: при работе с программами и приложениями разработчики часто используют позиционную систему счисления для представления данных и выполнения операций.
- Электроника: в электронных схемах и при работе с микроконтроллерами также используется позиционная система счисления.
Это лишь некоторые примеры применения позиционной системы счисления в технологиях. Благодаря своей универсальности и эффективности, она широко использовалась и продолжает использоваться в различных областях современных технологий.



