В геометрии понятие "проведение плоскости через точку" играет важную роль при изучении пространственных фигур и отношений между ними. Плоскость - это бесконечно тонкое плоское пространство, состоящее из всех точек, лежащих на одной и той же плоскости. Когда говорят, что плоскость проведена через точку А, это значит, что все точки этой плоскости лежат на одной линии с точкой А.
Представьте, что у вас есть точка А, которая лежит в пространстве. Если провести плоскость через эту точку, то все точки этой плоскости будут располагаться на одной прямой, которая проходит через точку А и перпендикулярна плоскости. Это означает, что существует бесконечное множество плоскостей, которые можно провести через данную точку.
Знание о том, что плоскость проведена через точку А, позволяет упрощать решение геометрических задач. Например, если нам нужно найти пересечение двух плоскостей и мы знаем, что обе плоскости проходят через одну и ту же точку А, то нам достаточно найти только одну общую точку, чтобы определить пересечение этих плоскостей в целом.
Определение понятий: точка и плоскость
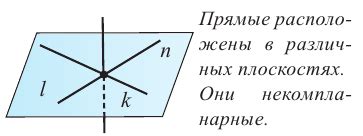
Плоскость - геометрическое понятие, представляющее собой бесконечно тонкую поверхность, которая содержит все возможные прямые, параллельные данной плоскости. Плоскость можно представить как двухмерное пространство, которое располагается на бесконечном расстоянии во всех направлениях.
Точка | Плоскость |
Через точку А (обозначается заглавной латинской буквой) может быть проведено бесконечное количество плоскостей. Плоскость, проходящая через точку А, называется плоскостью А.
Точка

В геометрии точка считается элементарной фигурой, относительно которой определяются другие геометрические объекты, такие как отрезки, прямые, плоскости и тела.
Точка может быть определена координатами на геометрической плоскости или в трехмерном пространстве. На плоскости точку обычно обозначают парой чисел, называемых координатами (x, y), где x - абсцисса (горизонтальное положение точки), а y - ордината (вертикальное положение точки).
Также, точка может быть представлена в виде геометрического символа - круга или точки на бумаге или экране компьютера.
Плоскость
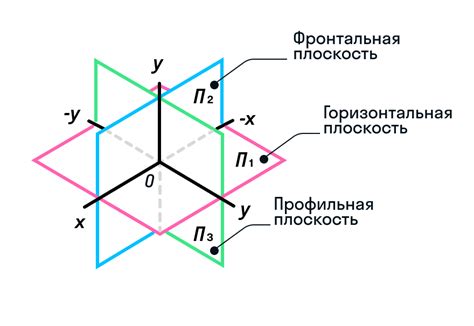
Через точку а может быть проведено бесконечное количество плоскостей. Плоскость, проходящая через точку, называется плоскостью, проходящей через данную точку.
Построение плоскости, проходящей через точку а, требует минимум трех точек. Эти точки должны быть неколлинеарными, то есть не лежать на одной прямой.
Зная координаты точки а и направляющие векторы плоскости, можно установить уравнение плоскости, проходящей через эту точку.
Значение проведения прямой через точку в плоскости

Проведение прямой через точку в плоскости имеет важное значение в геометрии. Это позволяет определить не только направление и угол наклона прямых, но и провести различные построения и находить точки пересечения.
Когда прямая проводится через точку в плоскости, она проходит ровно через эту точку и не имеет других ограничений. Такое построение позволяет нам определить направление прямой относительно точки. Можно сказать, что точка является началом или концом прямой в данной плоскости.
Зная направление прямой при проведении через точку, мы можем находить ее угол наклона. Для этого можно использовать геометрические инструменты, такие как угломер или протрактор. Также существуют математические методы для вычисления угла наклона прямой через точку с помощью тригонометрии.
Проведение прямой через точку также позволяет нам находить точки пересечения. Если у нас есть две прямые, проведенные через точки в плоскости, мы можем определить точку пересечения этих прямых. Это может быть полезно при решении геометрических задач или при построении графиков функций.
Таким образом, проведение прямой через точку в плоскости дает нам множество возможностей для определения направления, угла наклона и нахождения точек пересечения. Это важный инструмент в геометрии и математике в целом.
Проведение прямой через точку
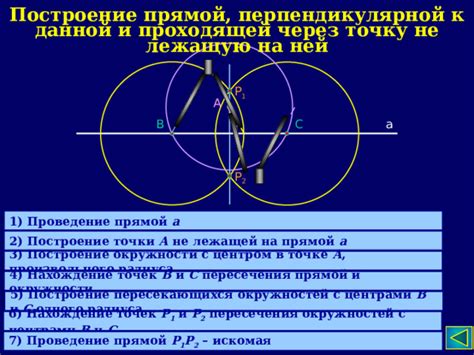
Для проведения прямой через точку нам понадобится еще одна точка и правило, которое поможет нам провести прямую таким образом, чтобы она точно пересекала выбранную точку А.
Если дана точка А и произвольная точка B, мы можем провести прямую AB таким образом, чтобы она пересекала точку А. Вектор, направленный от точки A к точке B, называется непосредственным направляющим вектором прямой AB. Он определяет направление прямой и является важной характеристикой данной прямой.
Используя непосредственно направляющий вектор, мы можем провести прямую через точку А. Для этого берем начальную точку А и перемещаемся в направлении данного вектора. Так мы получаем прямую, которая точно пересекает данную точку А.
Проведение прямой через точку используется во множестве геометрических задач. Зная точку А и непосредственно направляющий вектор, мы можем найти уравнение прямой, а также провести параллельную или перпендикулярную прямую через данную точку.
Математическое значение данного действия

Через точку А на плоскости можно провести бесконечно много плоскостей. Каждая такая плоскость будет иметь свои особенности и свойства.
Математически, проведение плоскости через точку А можно рассматривать как действие, при котором задается новая плоскость, проходящая через эту точку. Точка А является одной из бесконечно многих точек, которые лежат на данной плоскости.
Проведение плоскости через точку А может иметь различные цели и применения в математике. Например, при построении графиков функций можно проводить плоскость через оси координат и точку, которая соответствует заданной функции в определенной точке.
В геометрии проведение плоскости через точку А также может использоваться для определения взаимного расположения различных фигур. Например, проведение плоскости через вершину треугольника может помочь определить его тип и свойства.
Таким образом, проведение плоскости через точку А имеет математическое значение, которое заключается в задании новой плоскости, проходящей через данную точку, и использовании этой плоскости для решения геометрических или алгебраических задач.
Значение проведения плоскости через точку

Проведение плоскости через точку в геометрии имеет важное значение. Когда плоскость проводится через точку, она определяет направление вектора и позволяет установить взаимное расположение объектов.
Плоскость, проходящая через точку, может быть полезна при решении задач с трехмерной геометрией. Например, когда нужно определить, лежат ли две прямые в одной плоскости или пересекаются ли они в заданной точке. Проведение плоскости через точку помогает также при определении углов между прямыми или плоскостями.
Использование плоскости, проведенной через точку, также позволяет задать множество точек, лежащих на плоскости или в ее окрестности. Это может быть полезно при построении геометрических объектов, например, при построении окружности на плоскости или при определении местоположения точек в пространстве.
Проведение плоскости через точку является важным шагом при анализе и решении геометрических задач. Плоскость позволяет установить взаимное расположение объектов, определить углы и направления. Проведение плоскости через точку помогает строить и визуализировать геометрические объекты в трехмерном пространстве.
| Пример | Описание |
|---|---|
| Плоскость, проходящая через точку A | Позволяет определить, лежат ли прямые AB и AC в одной плоскости |
| Угол между прямыми, проходящими через точку A | Определяет величину и направление угла между прямыми AB и AC |
| Множество точек, лежащих на плоскости, проходящей через точку A | Определяет регион на плоскости, содержащий все возможные точки, которые могут принадлежать этой плоскости |





