Область определения функции – это множество всех значений, которые может принимать независимая переменная или аргумент функции. В контексте графиков функций область определения представляет собой множество всех возможных значений аргумента при рассмотрении функции.
График функции – это визуальное представление зависимости между независимой и зависимой переменными. Он позволяет наглядно увидеть, как меняется значение функции при изменении аргумента. Область определения функции на графике определяет, в каких точках графика функции существует и имеет смысл.
Например, если рассмотреть функцию f(x) = sqrt(x), то ее область определения не может содержать отрицательные числа или ноль, так как квадратный корень из отрицательного числа или нуля не существует в действительных числах. График функции будет представлять собой положительную часть оси абсцисс, где значение аргумента больше нуля.
Знание области определения функции на графике позволяет более точно анализировать поведение функции и ее свойства в различных точках. Также, зная область определения, можно определить допустимые значения аргумента и избежать ошибок при вычислениях.
Область определения функции
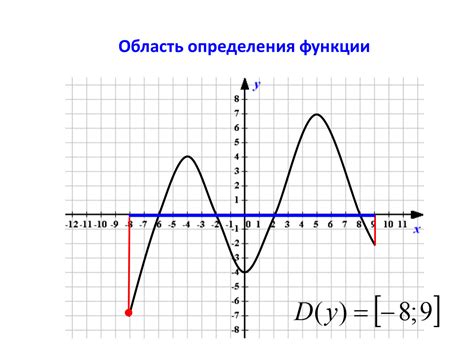
Область определения определяет правила, которые надо соблюдать при выборе значений аргумента функции. Некоторые значения могут быть недопустимыми, так как при них функция может принимать некорректное значение или не определена вовсе.
На графике функции область определения можно определить, просматривая ось аргумента. Значения, для которых функция определена, будут находиться на графике функции, в то время как значения, для которых функция не определена, будут вне графика.
Изучение области определения функции позволяет определить основные свойства функции и помогает в решении различных задач. Например, при построении графика функции, зная ее область определения, можно определить, какие части графика будут отображены, а какие – игнорироваться.
Важно отметить, что область определения функции может изменяться в зависимости от контекста задачи или допущений, сделанных в ее формулировке. Поэтому при работе с функциями необходимо учитывать указания и ограничения, заданные явно или неявно.
График функции
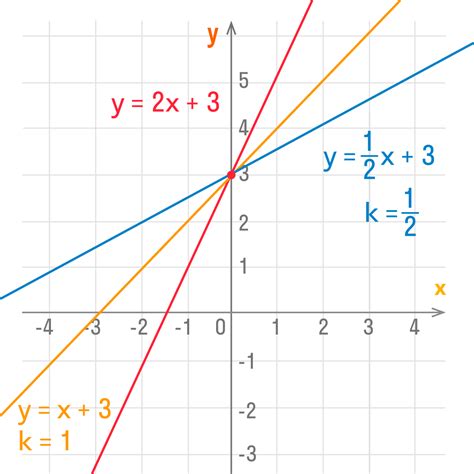
График функции обычно строится на координатной плоскости, где по горизонтальной оси откладываются значения аргумента функции, а по вертикальной оси - значения самой функции. Каждая точка на графике соответствует определенной паре значений аргумента и функции.
Область определения функции на графике - это множество значений аргумента, для которых функция имеет определенное значение. Все точки на графике, которые не относятся к области определения функции, не будут иметь смысла и могут считаться недействительными. Область определения функции на графике можно определить по его особенностям, таким как периодичность, асимптоты, точки разрыва и другим характеристикам.
Анализ графика функции помогает понять ее свойства и поведение, такие как возрастание, убывание, наличие экстремумов и точек перегиба. Понимание графика функции позволяет решать различные задачи, связанные с этой функцией, и устанавливать связи между этой функцией и другими.
Определение на графике
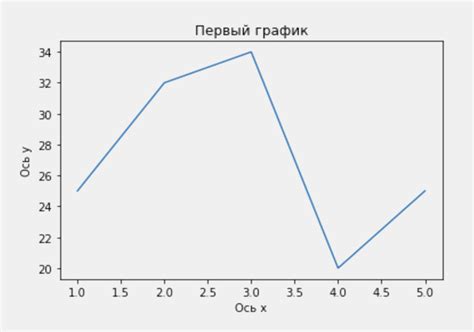
Область определения функции на графике представляет собой множество всех значений аргументов, при которых функция имеет определение и может быть вычислена. Математически, область определения функции на графике можно представить в виде интервалов или конечных множеств.
На графике функции область определения может быть определена по оси аргументов, где значения аргументов указываются вдоль оси X. То есть, на графике видно, на каких значениях X функция имеет определение.
Область определения на графике может быть ограничена либо неограничена. Если график функции охватывает всю ось X без каких-либо пропусков, то область определения функции является неограниченной. Если же график функции ограничен на определенном интервале, то область определения функции является ограниченной.
Определение на графике функции позволяет определить, при каких значениях аргументов функция существует и возможно вычисление ее значений. Это важная информация при изучении и анализе функций для определения их свойств и поведения.



