Математика - это наука о числах, фигурах и структурах. Одним из основных понятий, изучаемых в школьной программе по математике, является понятие значения.
Значение - это числовое выражение, которое показывает, какое число соответствует определенному выражению или переменной. Другими словами, это результат вычисления выражения или математической операции.
В пятом классе одним из первых понятий, связанных с значением, является значение выражения, которое вычисляется путем подстановки чисел вместо переменных. Например, если у нас есть выражение 2x + 5, где x - переменная, то значение этого выражения при x=3 будет 2*3 + 5 = 6 + 5 = 11.
Значение - очень важное понятие в математике, так как оно помогает понять, как работать с выражениями и уравнениями. Знание значений помогает ученикам понять, какие числа соответствуют определенным выражениям и как сравнивать их между собой. Это важно для решения различных задач и применения математики в повседневной жизни.
Понимание понятия значения в математике является фундаментом для дальнейшего изучения более сложных тем, таких как уравнения, системы уравнений и функции. Поэтому важно усвоить основные принципы вычисления значений в 5 классе, чтобы иметь надежную основу для дальнейшего изучения математики.
Математика 5 класс: значение и его смысл

Значение числового выражения можно найти, подставив в него конкретные числа. Например, для выражения 2 + 3 значение будет равно 5, так как при сложении 2 и 3 получается 5.
Важно понимать, что значение выражения может быть как положительным, так и отрицательным. Например, если мы вычисляем значение выражения 5 - 7, то получаем -2, что означает, что число 5 меньше числа 7 на 2.
Арифметические функции, такие как сложение, вычитание, умножение и деление, также имеют значение. Например, при умножении 4 на 6 получается значение 24.
В алгебре функции также имеют значение, которое зависит от значения переменных. Например, если функция y = 2x + 3, то значение этой функции при x = 4 будет равно 11, так как при подстановке 4 вместо переменной x получается 2 * 4 + 3 = 11.
Значение в математике имеет свой смысл и помогает нам понять, как влияют различные операции и переменные на результат.
Значение - основа математики 5 класса

Значение необходимо для определения порядка чисел. Меньшее число имеет меньшее значение, а большее число - большее. Например, число -5 имеет меньшее значение, чем число 2, так как оно находится левее на числовой прямой.
Значение числа можно определить с помощью числовой прямой и числового отрезка. На числовой прямой значения чисел обозначаются точкой. Например, точка с координатой -5 обозначает число -5.
Значение числа положительно, если оно находится правее нуля на числовой прямой. Значение числа отрицательно, если оно находится левее нуля на числовой прямой.
Значение числа можно также представить в виде числового отрезка, где число 0 находится в середине, положительные числа располагаются справа, а отрицательные числа - слева. Например, числа от -5 до 5 образуют числовой отрезок.
Значение является важным понятием при решении математических задач, так как позволяет сравнивать числа и определять их порядок. Например, при сравнении двух чисел нужно определить, какое из них имеет большее значение.
Понятие значения в математике 5 класс

В 5 классе, дети начинают изучать различные математические выражения и функции, и определять их значения. Например, пусть есть выражение 3 + 4. Чтобы найти его значение, нужно сложить числа 3 и 4, что приведет к результату 7.
Еще один пример - функция. Функция - это соответствие между элементами двух множеств, где каждому элементу одного множества сопоставляется элемент другого множества. Понятие функции вводится в 5 классе. Чтобы найти значение функции, нужно подставить значение аргумента в формулу функции. Например, пусть есть функция f(x) = 2x + 3 и аргумент x = 5. Чтобы найти значение функции f(5), нужно подставить x = 5 в формулу: f(5) = 2 * 5 + 3 = 13.
Понимание значения в математике важно, так как оно позволяет понять результаты вычислений и решений задач. Умение находить значение выражений и функций помогает решать различные задачи и применять математику в повседневной жизни.
Значение числа и его роль в математике 5 класса
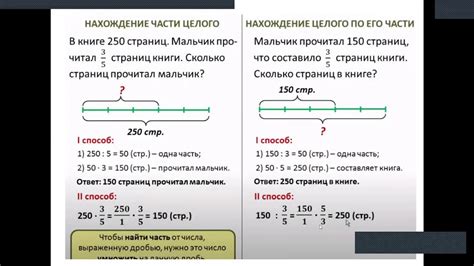
Числа играют важную роль в математике и имеют свои значения, которые используются для описания количества или позиции объектов.
Значение числа зависит от его разряда и положения в числовой системе. Например, число 345 состоит из трех разрядов: сотни (3), десятки (4) и единицы (5). В данном случае, значение каждого разряда можно выразить как произведение цифры на степень десятки. Таким образом, значение числа 345 будет равно: 3 × 100 + 4 × 10 + 5 × 1 = 345.
Кроме того, числа могут иметь различные значения в зависимости от контекста. Например, число 5 может означать пять яблок или пять метров. Поэтому, в математике важно уметь интерпретировать значение числа в соответствии с задачей или ситуацией.
Значение числа также может быть отрицательным или положительным, что указывает на его направление или удаленность от нуля на числовой оси. Например, число -2 означает, что объект находится две единицы влево от нулевой точки на числовой оси.
Значение переменной и его применение в математике 5 класса

В математике 5 класса мы часто сталкиваемся с понятием переменной. Значение переменной представляет собой число или выражение, которое может меняться в зависимости от условий задачи или выбора.
В уравнениях и выражениях, переменные обозначаются буквами, такими как "x" или "y". Значения переменных могут быть определены числами или выражениями.
Применение переменных в математике 5 класса позволяет решать задачи и находить неизвестные значения. Мы можем использовать переменные для записи и решения уравнений, составления и анализа выражений, а также для решения задач на изменение и зависимости величин.
Например, мы можем использовать переменную "x" для представления неизвестного возраста человека. Если мы знаем, что взрослый человек должен быть старше 18 лет, то можем записать условие: x > 18. Задача состоит в том, чтобы найти значение переменной "x", которое удовлетворяет данному условию.
Также переменные могут использоваться для составления и решения простых уравнений. Например, уравнение 2x + 5 = 15 означает, что двукратное значение переменной "x", увеличенное на 5, равно 15. Мы можем найти значение переменной "x", выполнив необходимые действия: 2x = 15 - 5; 2x = 10; x = 5.
Значение переменной в математике 5 класса имеет важное значение для решения задач и анализа математических выражений. Работа с переменными помогает детям развивать логическое мышление, умение анализировать и решать проблемы, а также повышает абстрактное и алгоритмическое мышление.
Значение операции и ее значение в математике 5 класса

Значение операции в математике означает результат выполнения этой операции. В пятом классе ученики изучают различные операции, такие как сложение, вычитание, умножение и деление.
Значение сложения – это сумма двух или более чисел. Например, если сложить 3 и 5, то значение этой операции будет равно 8.
Значение вычитания – это разность двух чисел. Например, если вычесть 4 из 9, то значение такой операции будет равно 5.
Значение умножения – это произведение двух или более чисел. Например, если умножить 2 на 6, то получится значение, равное 12.
Значение деления – это частное, получающееся при делении одного числа на другое. Например, если разделить 10 на 2, то значение такой операции будет равно 5.
Важно понимать, что значение операции зависит от исходных чисел и может изменяться в зависимости от них. Например, сложение двух положительных чисел даст положительное значение, а сложение положительного и отрицательного чисел может дать как положительное, так и отрицательное значение.
Ученики пятого класса изучают основные принципы и понятия математики, включая значение операций, что позволяет им решать простые математические задачи и развивать логическое и аналитическое мышление.
Значение выражения и его значимость в математике 5 класса

Значение выражения можно найти, следуя определенной последовательности действий. Сначала нужно заменить переменные в выражении конкретными числами, которые указаны в условии задачи или известны из других источников. Затем необходимо выполнить арифметические операции, указанные в выражении, в соответствии с приоритетом операций. В конечном итоге получается числовое значение, которое и является значением самого выражения.
Понимание значения выражения в математике 5 класса важно для решения задач и общего понимания математического материала. Знание как найти значение выражения и его правильное использование помогает ученикам развивать логическое мышление и аналитические навыки, а также повышает их успехи в учебе.
В итоге, значение выражения является ключевым понятием в математике 5 класса, которое помогает ученикам решать задачи, сравнивать выражения и развивать навыки анализа и логического мышления. Понимание значения выражения открывает двери к пониманию более сложных математических концепций и помогает строить крепкую основу для дальнейшего изучения математики.
Значение функции и ее значение в математике 5 класса

Чтобы найти значение функции, нужно подставить значение аргумента в выражение функции и вычислить его. Например, если дано выражение функции f(x) = x + 3 и нужно найти значение функции для x = 2, то нужно подставить 2 вместо x и выполнить вычисление: f(2) = 2 + 3 = 5. Таким образом, значение функции для данного случая равно 5.
Значение функции может быть как числовым, так и графическим. Например, при построении графика функции можно найти значение функции для определенного значения аргумента, считая его высоту над горизонтальной осью.
Значение функции в математике 5 класса часто используется для решения различных задач, например, для нахождения корней уравнений или определения области определения функции.
Таким образом, понимание значения функции и ее значение в математике 5 класса является ключевым для успешного решения математических задач и понимания более сложных понятий в будущем.
Значение уравнения и его роль в математике 5 класса
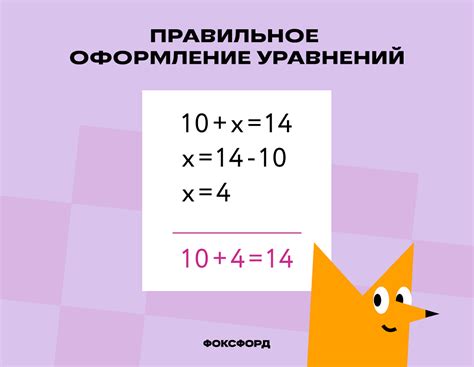
Примером уравнения может служить простейшее уравнение вида 2x + 5 = 15. Для того чтобы найти значение переменной x, необходимо решить это уравнение. Подставив различные значения для x, мы можем проверить, при каком значении уравнение становится верным. В данном случае, если мы подставим x = 5, то уравнение станет верным: 2 * 5 + 5 = 15. Таким образом, значение уравнения равно 5.
Значение уравнения имеет большое значение в математике, так как позволяет находить неизвестные переменные и решать различные задачи. В 5 классе дети изучают простые уравнения с одной неизвестной, которые помогают развивать логическое мышление, аналитические способности и навыки работы с числами.
Для решения уравнений в 5 классе можно использовать различные методы, такие как прямое подстановка значений, выявление общего множителя или решение уравнения пошагово. Знание значений уравнения поможет детям успешно справляться с упражнениями и заданиями по математике и приобретать необходимые навыки для дальнейшего изучения предмета.
| Пример | Значение уравнения | Решение |
|---|---|---|
| 2x + 5 = 15 | 5 | 2 * 5 + 5 = 15 |
| 3 + y = 10 | 7 | 3 + 7 = 10 |
| 4a - 2 = 10 | 3 | 4 * 3 - 2 = 10 |
Значение неравенства и его применение в математике 5 класса

В 5 классе, ученики знакомятся с понятием неравенства и его применением в различных математических задачах. Они учатся сравнивать числа и определять их отношение друг к другу с помощью неравенств.
Кроме того, ученики учатся работать с неравенствами в математических уравнениях и неравенствах. Они учатся решать неравенства и находить значения переменных, удовлетворяющие данному неравенству.
Таким образом, знание о значении неравенства и его применение помогают ученикам развивать навыки сравнения чисел, решения математических задач и работы с уравнениями и неравенствами.



