Выпуклый многоугольник - это такой многоугольник, все углы которого являются выпуклыми, то есть сумма всех внутренних углов многоугольника больше 180 градусов. В 8 классе учащиеся изучают понятие выпуклого многоугольника, а также его свойства.
Выпуклый многоугольник имеет ряд характерных свойств. Например, все диагонали выпуклого многоугольника лежат внутри него. Это значит, что любая прямая, соединяющая две точки внутри многоугольника, полностью лежит внутри его границы. Также выпуклый многоугольник имеет наибольшее площадь среди всех многоугольников с теми же вершинами.
Учащиеся 8 класса также изучают условия, которые должны выполняться для определения выпуклого многоугольника, такие как неравенство всех внутренних углов многоугольника. Они также учатся классифицировать многоугольники на выпуклые и невыпуклые, что помогает им лучше понять структуру и свойства этих геометрических фигур.
Определение выпуклого многоугольника
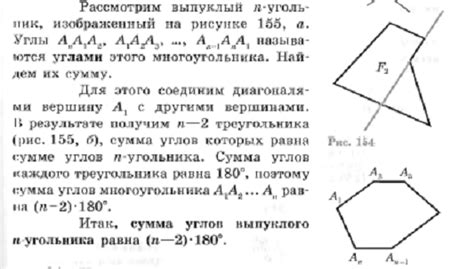
Выпуклый многоугольник – это многоугольник, все внутренние углы которого являются выпуклыми, то есть они меньше 180 градусов. Основное свойство выпуклого многоугольника заключается в том, что любая прямая, проведенная внутри данного многоугольника, не пересекает его сторон и углы. Другими словами, выпуклый многоугольник не имеет "вдавленных" частей, все его стороны выгнуты наружу.
Для определения выпуклого многоугольника можно использовать следующий критерий: если для любых двух подряд идущих вершин и любой другой точки, лежащей внутри многоугольника, прямая, соединяющая первую вершину с данной точкой, не пересекает многоугольник, то многоугольник является выпуклым.
Выпуклые многоугольники широко применяются в геометрии, как в теоретических задачах, так и в практических решениях. Они обладают множеством свойств, которые позволяют легко проводить различные операции с ними, такие как нахождение периметра и площади, разделение на треугольники и многое другое.
Понятие выпуклого многоугольника
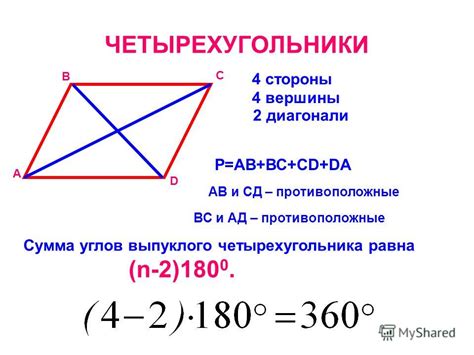
Чтобы понять, что такое выпуклый многоугольник, нужно представить себе многоугольник на плоскости и провести через любые две его вершины прямую. Если эта прямая не пересекает многоугольник, то он является выпуклым. Однако, в случае пересечения или касания прямой с многоугольником, он будет невыпуклым.
Выпуклые многоугольники обладают рядом свойств:
- Внутренние углы выпуклого многоугольника не превосходят значения 180 градусов. Более того, все внутренние углы выпуклого многоугольника строго меньше значения 180 градусов.
- Любая прямая, проходящая через две вершины выпуклого многоугольника, лежит полностью внутри многоугольника, за исключением самих вершин.
- Выпуклый многоугольник имеет только один внутренний угол в каждой своей вершине.
- Выпуклый многоугольник не имеет самопересечений, то есть отрезки, соединяющие две вершины, не пересекаются внутри многоугольника.
Выпуклые многоугольники широко применяются в различных областях, таких как геометрия, компьютерная графика и оптимизация. Знание и понимание понятия выпуклого многоугольника позволяет лучше анализировать и работать с такими многоугольниками в этих областях.
Свойства выпуклого многоугольника
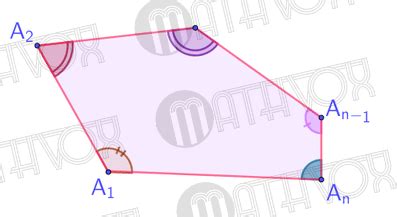
1. Углы выпуклого многоугольника
В каждой вершине выпуклого многоугольника сумма внутренних углов всегда равна 180 градусам. То есть, если у данного многоугольника n вершин, то сумма его внутренних углов равна (n-2) * 180°.
2. Ребра выпуклого многоугольника
Ребра выпуклого многоугольника не пересекаются. Каждое ребро соединяет две вершины и лежит полностью внутри многоугольника.
3. Диагонали выпуклого многоугольника
Диагонали выпуклого многоугольника соединяют две вершины, не являющиеся соседними. Каждая диагональ полностью лежит внутри многоугольника и не пересекает никакие его ребра.
4. Центр симметрии
В любом выпуклом многоугольнике всегда существует точка, называемая центром симметрии, через которую можно провести ось симметрии, так что при отражении фигуры относительно этой оси она совпадает сама с собой. Центр симметрии многоугольника совпадает с его центром тяжести.
5. Периметр и площадь
Периметр выпуклого многоугольника равен сумме длин всех его сторон. Площадь многоугольника равна сумме площадей всех его треугольников (если отметить внутри многоугольника точку и соединить ее с каждой вершиной).
Знание этих свойств помогает в анализе и решении задач, связанных с выпуклыми многоугольниками, а также с их конструкцией и характеристиками.
Виды выпуклых многоугольников
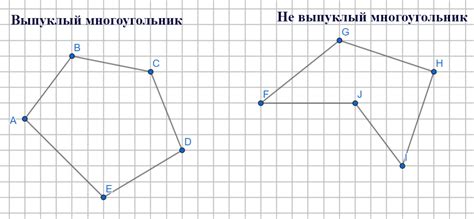
Выпуклый многоугольник представляет собой фигуру, все вершины которой лежат в одной плоскости и все углы внутри нее не превышают 180 градусов. Однако выпуклые многоугольники бывают различных видов, которые обладают своими особенностями и характеристиками.
1. Простой выпуклый многоугольник. Простым называется выпуклый многоугольник, вершины которого не пересекаются и не лежат на одной прямой. Такой многоугольник образуется только из одного контура.
2. Невыпуклый многоугольник. Невыпуклым называется такой многоугольник, у которого имеется хотя бы один выдавленный угол или пересекающиеся стороны. В отличие от выпуклого многоугольника, вершины невыпуклого многоугольника могут лежать на одной прямой.
3. Многоугольник с самопересечениями. В этом случае у многоугольника имеются пересекающиеся стороны с образованием самопересечений. Такие многоугольники могут иметь любую форму и не являются допустимыми при определении выпуклого многоугольника.
4. Окружность. Окружность также является выпуклым многоугольником, но имеет особые свойства. Все точки окружности равноудалены от центра, а углы внутри нее равны 180 градусов.
Знание о видах выпуклых многоугольников позволяет анализировать и классифицировать их по различным свойствам, а также применять полученные знания в решении разнообразных геометрических задач.
Примеры выпуклых многоугольников
Рассмотрим несколько примеров выпуклых многоугольников:
Многоугольник с 4 вершинами | Многоугольник с 5 вершинами |
Многоугольник с 6 вершинами | Многоугольник с 8 вершинами |
В этих примерах все углы каждого многоугольника меньше 180 градусов, и все его вершины лежат на одной выпуклой оболочке.
Применение выпуклых многоугольников в реальных задачах

| Дисциплина | Пример применения |
|---|---|
| География | Определение границ территории, выявление контуров географических объектов. |
| Робототехника | Планирование движения роботов, избегание препятствий на основе определения выпуклых областей. |
| Компьютерная графика | Рендеринг трехмерных объектов, определение линейной перспективы. |
| Экономика | Моделирование проблем распределения ресурсов, определение оптимальных маршрутов доставки. |
| Оптимизация задач | Поиск максимально эффективного способа решения задач с ограничениями. |
И это только небольшая часть областей, где выпуклые многоугольники находят свое применение. Изучение и понимание свойств этих фигур помогает в решении разнообразных задач и развитии абстрактного мышления. Поэтому знакомство с выпуклыми многоугольниками в 8 классе – важный этап в обучении геометрии и аналитической геометрии.







