Вектор - это понятие, которое используется в математике и физике для описания направления и величины движения или силы.
Вектор задается двумя характеристиками: направлением и модулем, или величиной. Направление вектора определяется углом между его направлением и некоторой фиксированной осью. Модуль вектора, или его длина, определяется числовым значением. Векторы используются в различных областях науки и техники, таких как физика, геометрия, программирование и т. д.
Векторы могут быть разных типов в зависимости от своих свойств и применения. Одним из наиболее распространенных типов является геометрический вектор. Геометрический вектор задает направление и длину смещения от начальной точки к конечной точке. Он используется для описания перемещения, скорости, ускорения и других физических величин.
Кроме того, существуют алгебраические векторы, которые представляют собой упорядоченные наборы чисел, называемых компонентами или координатами. Алгебраические векторы используются для описания различных физических и математических величин, таких как сила, скорость, ускорение, скалярное и векторное произведение.
Кроме геометрических и алгебраических векторов существуют еще и другие типы векторов, такие как единичные векторы, нулевые векторы и свободные векторы. Единичные векторы имеют длину равную 1 и используются для задания направления. Нулевые векторы имеют нулевую длину и не имеют определенного направления. Свободные векторы представляют собой векторы, которые не имеют фиксированной точки приложения и могут перемещаться в пространстве.
Определение и примеры векторов

Вектор может быть задан различными способами:
- С использованием координат: координатами начала и конца вектора.
- С использованием компонентов: проекциями вектора на координатные оси.
- С помощью направляющих чисел: числами, которые задают направление и длину вектора.
Примеры векторов:
- Вектор скорости: указывает направление и скорость движения тела.
- Вектор силы: определяет направление и величину действующей силы.
- Вектор смещения: представляет собой разницу между начальным и конечным положением объекта.
- Вектор ускорения: показывает изменение скорости объекта.
Структура вектора и его характеристики

Вектор представляет собой математическую сущность, которая используется для описания физических и геометрических величин. Он характеризуется не только своим числовым значением, но и направлением.
Структура вектора состоит из двух основных компонентов: модуля и направления. Модуль вектора представляет собой его длину и указывает на величину данного вектора. Направление вектора определяется углом, который образует вектор с заданной осью или направлением.
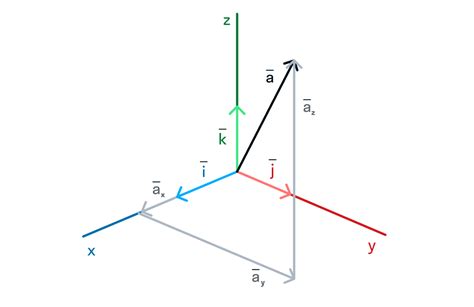
Векторы могут быть двумерными или трехмерными, в зависимости от количества компонентов, которые они имеют. Двумерные векторы обычно представлены в виде упорядоченных пар чисел (x, y) или векторов. Трехмерные векторы могут быть представлены в виде упорядоченных троек чисел (x, y, z) или векторов.
У векторов также есть различные характеристики, такие как сумма и разность векторов, скалярное и векторное произведение. Сумма векторов представляет собой операцию, при которой соответствующие компоненты векторов суммируются. Разность векторов осуществляется путем вычитания соответствующих компонентов одного вектора из компонентов другого вектора.
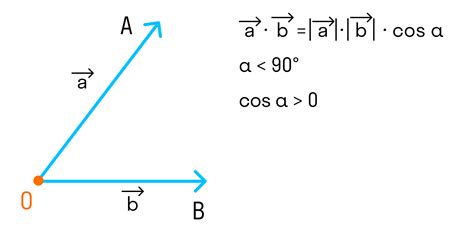
Скалярное произведение векторов представляет собой операцию, при которой перемножаются все соответствующие компоненты векторов, а затем результаты суммируются. Скалярное произведение часто используется для нахождения угла между векторами или для определения проекции одного вектора на другой.
Векторное произведение векторов представляет собой операцию, при которой находится новый вектор, перпендикулярный обоим исходным векторам. Векторное произведение также используется для нахождения площади параллелограмма, образованного двумя исходными векторами.
Векторы играют важную роль во многих областях науки, техники и геометрии. Они позволяют более точно описывать и моделировать различные физические и геометрические явления, а также являются основой для множества вычислительных методов и алгоритмов.
Скалярный вектор и его использование
Скалярные векторы широко используются в различных областях, включая физику, математику и компьютерную графику. Они могут быть использованы для представления физических величин, таких как скорость, масса или температура.
В физике, например, скалярные векторы используются для описания величин, которые имеют только численное значение, такие как энергия или время. Они обычно обозначаются буквой с нижним индексом, такой как E или t.
В математике скалярные векторы могут быть использованы в различных операциях, таких как сложение и умножение на скаляр. Они также могут быть использованы в линейной алгебре для решения уравнений и систем уравнений.
Скалярные векторы также используются в компьютерной графике для определения положения объектов на экране. Они могут быть использованы для определения координат точек и векторов, а также для задания расстояния между объектами.
| Примеры скалярных векторов | Обозначение |
|---|---|
| Скорость автомобиля | v |
| Масса объекта | m |
| Температура воздуха | T |
| Высота здания | h |
В целом, скалярные векторы играют важную роль в многих областях науки и техники. Их использование позволяет точно определить и описать различные физические и математические величины, что делает их неотъемлемой частью нашей повседневной жизни.
Нулевой вектор и его свойства

Основными свойствами нулевого вектора являются:
- Нулевой вектор является нейтральным элементом по отношению к операции сложения векторов. Это означает, что при сложении нулевого вектора с любым другим вектором получится сам этот вектор: 0 + a = a, где a – произвольный вектор.
- Нулевой вектор является нейтральным элементом по отношению к операции вычитания векторов. Это означает, что при вычитании нулевого вектора из любого другого вектора получится сам этот вектор: a - 0 = a, где a – произвольный вектор.
- Нулевой вектор является нулевым элементом по отношению к операции умножения вектора на число. Это означает, что умножение нулевого вектора на любое число дает нулевой вектор: k * 0 = 0, где k – произвольное число.
Нулевой вектор не имеет определенного направления, поэтому его иногда можно представить как точку в пространстве. Векторы, отличные от нулевого, называют ненулевыми векторами.
Единичный вектор и его особенности

Векторы могут быть представлены в виде направленных отрезков на плоскости или в пространстве. Их длина показывает, насколько велик физический или геометрический объект, который они представляют. Однако, длина вектора сама по себе не несет большого значения, пока не будет установлено направление, в котором он указывает.
Единичный вектор имеет длину, равную 1, но его основное значение заключается в его направлении. Он является нормализованной формой вектора, так как позволяет сосредоточиться только на направлении, не обращая внимания на его масштаб или длину.
Единичный вектор также важен, когда речь идет о различных операциях над векторами, таких как скалярное произведение и векторное произведение. Например, проекция вектора на другой вектор может быть найдена путем умножения длины этого вектора на косинус угла между ними. Единичный вектор также удобен для определения угла между векторами.
Применение единичного вектора распространено в различных областях науки и техники, включая физику, геометрию, компьютерную графику, робототехнику, аэронавтику и даже игровую индустрию. Он является важным инструментом для анализа и моделирования движений объектов в пространстве и определения результатов взаимодействий между ними.
Таким образом, единичный вектор является ключевым понятием в векторной алгебре и играет значительную роль в решении различных задач. Он позволяет упростить вычисления и упрощает анализ физических и геометрических явлений, что делает его ориентирами во многих областях науки и техники.
Свободный вектор и его свойства
Свободный вектор – это вектор, который может быть перемещен и повернут в пространстве без изменения своих свойств. Он не привязан к определенной точке или началу координат, и его положение может быть произвольно выбрано. Свободный вектор представляет собой только направление и длину, но не имеет никаких абсолютных или фиксированных координат.
Свободный вектор можно представить в виде направленного отрезка, где начальная точка и конечная точка не важны, поскольку вектор сохранит свое направление и длину при перемещении.
Основные свойства свободного вектора:
- Сложение: Свободные векторы могут быть складываны между собой. Результат сложения будет новым свободным вектором с направлением и длиной, определенными в соответствии с законами векторной алгебры.
- Умножение на число: Свободный вектор может быть умножен на скаляр (число). Произведение будет новым свободным вектором, который имеет ту же направленность, но измененную длину в соответствии с коэффициентом умножения.
- Противоположный вектор: Каждый свободный вектор имеет свой противоположный вектор, который имеет ту же направленность, но противоположную длину.
Свободные векторы широко применяются в физике, геометрии, инженерии и других науках для моделирования и анализа физических явлений и объектов, которые подчиняются законам векторной алгебры.
Коллинеарные векторы и их применение

Применение коллинеарных векторов встречается во многих областях науки и техники. Одним из применений является геометрия, где коллинеарные векторы используются для определения прямых или плоскостей. Например, для определения уравнения прямой, проходящей через две точки, можно использовать коллинеарные векторы.
Векторы с коллинеарными направлениями также часто применяются в физике. Например, векторы силы и ускорения могут быть коллинеарными, что облегчает расчеты в задачах механики.
Еще одним применением коллинеарных векторов является анализ данных. Возможность сравнивать векторы с коллинеарными направлениями может помочь выявить закономерности или тренды в наборе данных.
Изучение коллинеарных векторов и их применение имеет большое значение в различных областях науки и техники. Понимание свойств и характеристик коллинеарных векторов позволяет более точно и эффективно решать разнообразные задачи и проблемы.
Ортогональные векторы и их связь

Скалярное произведение векторов определяется суммой произведений их соответствующих координат. Если результат равен нулю, то говорят, что векторы ортогональны.
Ортогональные векторы играют важную роль в различных областях, таких как физика и геометрия. Они используются для построения трехмерных моделей, в решении уравнений и векторных операций.
Ортогональные векторы часто используются для определения базиса в векторном пространстве. Они образуют линейно независимую систему, что позволяет представлять любой вектор как линейную комбинацию ортогональных векторов.
Связь между ортогональными векторами проявляется в том, что они направлены в разные стороны. Если векторы имеют одинаковую длину, то они называются ортонормированными векторами.
Ортогональность векторов играет важную роль в линейной алгебре и математике в целом. Понимание свойств ортогональных векторов позволяет решать сложные задачи и упрощать вычисления.
Векторное пространство и его особенности
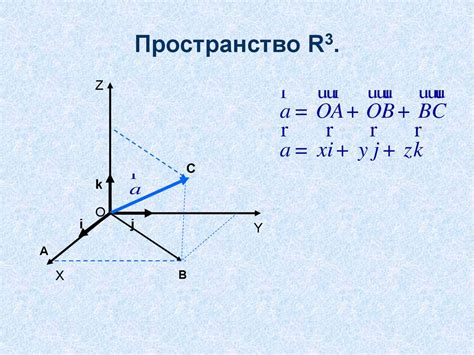
Особенности векторного пространства:
- Замкнутость относительно сложения – сумма двух векторов, принадлежащих векторному пространству, также принадлежит этому пространству. При сложении векторов не возникает никаких ограничений или ограничивающих условий. Это значит, что сумма может быть любым вектором из данного векторного пространства.
- Замкнутость относительно умножения на скаляр – умножение вектора на скаляр дает вектор, принадлежащий этому же векторному пространству. То есть, если вектор принадлежит векторному пространству, то произведение вектора на любой скаляр также будет принадлежать этому пространству.
- Ассоциативность операции сложения – результат сложения векторов не зависит от порядка, в котором их складывают. То есть, сложение векторов ассоциативно.
- Наличие нулевого вектора – в векторном пространстве всегда существует нулевой вектор, который при сложении с любым другим вектором не меняет его.
- Обратимость сложения – для каждого вектора в векторном пространстве найдется обратный вектор, такой, что их сумма будет равна нулевому вектору.
- Ассоциативность операции умножения на скаляр – произведение вектора на скаляр не зависит от порядка, в котором эти операции выполняются.
- Дистрибутивность операции умножения на скаляр относительно операции сложения – умножение вектора на скаляр, а потом сложение полученных результатов, равносильно сложению векторов, а потом умножению полученной суммы на тот же скаляр.
Векторное пространство находит применение во многих разделах математики, физики и других науках. Оно позволяет описывать и анализировать различные объекты, имеющие направление и величину, а также разрабатывать эффективные алгоритмы и модели, использующие векторные операции.



