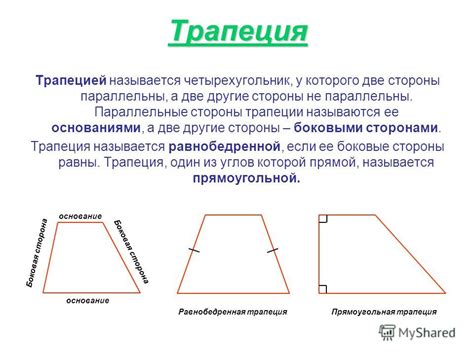
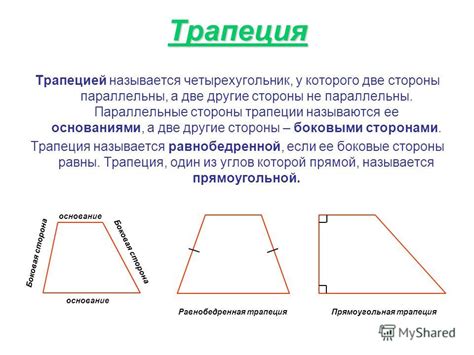
Трапеция - это геометрическая фигура, которая обладает множеством интересных свойств. Трапеция имеет четыре стороны: две параллельные стороны называются основаниями, а две другие стороны - боковыми сторонами. Мы можем наблюдать трапеции в жизни на примере различных объектов, таких как дорожные знаки, столы или пирамидки для игры.
Одним из важных свойств трапеции является то, что сумма всех ее углов равна 360 градусов. Боковые стороны трапеции могут быть либо одинаковой длины, либо различной длины. Кроме того, высота трапеции - это отрезок, который проходит перпендикулярно между параллельными основаниями и соединяет их.
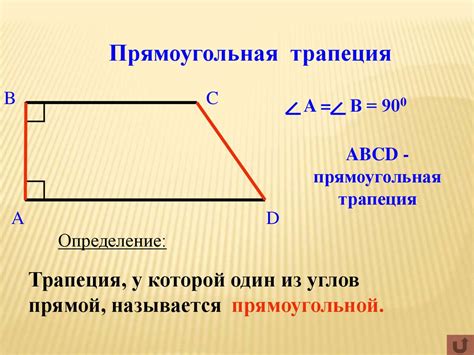
Также важно отметить, что трапеция является частным случаем параллелограмма - это плоская фигура, у которой противоположные стороны параллельны и равны. В общем случае, трапеция может быть прямоугольной, равнобедренной или произвольной. Прямоугольная трапеция - это такая трапеция, у которой один из углов равен 90 градусов.
Трапеция имеет много других интересных свойств, которые могут быть использованы в геометрии и математике. Например, альтернативные углы трапеции равны, а сумма углов при основаниях трапеции также равна 180 градусов. Знание свойств трапеции помогает решать различные задачи, связанные с этой фигурой и ее особенностями.
Что такое трапеция: определение и его свойства
Одно из оснований трапеции может быть длиннее другого, что определяет ее тип:
Прямоугольная трапеция - трапеция, у которой одно из оснований перпендикулярно боковым сторонам.
Равнобедренная трапеция - трапеция, у которой боковые стороны равны по длине.
Прямоугольная равнобедренная трапеция - трапеция, сочетающая в себе свойства прямоугольной и равнобедренной трапеции.
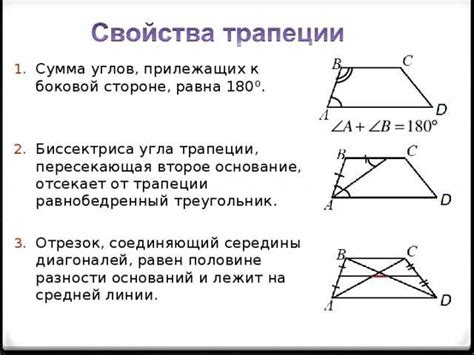
У трапеции есть несколько свойств:
- Сумма углов трапеции равна 360 градусам.
- Противоположные углы трапеции сумма которых равна 180 градусов, являются смежными или дополнительными.
- Высота трапеции - это перпендикуляр, опущенный из одного основания на другое. Она является ортогональной прямой к основаниям.
- Площадь трапеции можно вычислить, используя формулу: S = (a + b) * h / 2, где a и b - длины оснований, а h - высота.
- Периметр трапеции вычисляется по формуле: P = a + b + c + d, где a, b, c и d - длины сторон трапеции.
Трапеции встречаются в различных сферах, таких как геометрия, архитектура, инженерное дело, физика и т.д. Знание свойств трапеции помогает в решении задач, связанных с измерениями и конструкциями.
Определение трапеции
Также важно отметить, что все диагонали трапеции делятся пополам и пересекаются в точке, называемой точкой пересечения диагоналей. Трапеция обладает несколькими свойствами, такими как сумма всех ее углов равна 360 градусам и сумма длин ее противоположных сторон равна.
- Трапеция может быть вписана в окружность и в этом случае сумма углов на основаниях равна 180 градусам.
- Высотой трапеции называется расстояние между ее основаниями, и она является перпендикулярной к основаниям.
- Площадь трапеции рассчитывается по формуле: S = ((a + b) * h) / 2, где a и b – длины оснований, а h – высота.
Трапеции встречаются во многих областях геометрии и имеют широкое применение в решении различных задач, связанных с площадями и длинами. Изучение свойств и формул, связанных с трапециями, позволяет более глубоко понять структуру этой фигуры и применять полученные знания в практических ситуациях.
Стороны трапеции
В трапеции есть несколько основных сторон:
| Сторона | Название | Описание |
|---|---|---|
| AB | Основание | Это одна из параллельных сторон трапеции. Основание обычно обозначается буквами A и B. |
| CD | Основание | Это вторая параллельная сторона трапеции. Основание обычно обозначается буквами C и D. |
| BC | Боковая сторона | Это сторона, которая соединяет точки B и C и не является параллельной основаниям. |
| AD | Боковая сторона | Это сторона, которая соединяет точки A и D и не является параллельной основаниям. |
Из свойств трапеции следует, что основания равны между собой, то есть AB = CD. Боковые стороны могут быть равны или неравны, в зависимости от формы трапеции.
Знание названий и свойств основных сторон трапеции помогает упрощать и решать задачи по геометрии, а также улучшает понимание этой фигуры.
Углы трапеции

1. Углы основания: основания трапеции - это его параллельные стороны. Углы, образованные основаниями и боковыми сторонами, называются углами основания. В трапеции существуют два угла основания.
2. Смежные углы: это углы, которые расположены по соседству друг с другом в трапеции. Соседние углы соответствуют смежным углам.
3. Угол диагонали: это угол, образованный прямой, соединяющей вершины непараллельных сторон трапеции.
Зная эти основные типы углов трапеции, мы можем легче изучить ее свойства и использовать их в решении различных задач.
Основания трапеции
Основания трапеции можно представить как две равные параллельные отрезки, соединенные непараллельными сторонами. Длины оснований трапеции обозначаются как a и b.
На основании свойств трапеции можно выделить следующие особенности:
| 1. | Основания трапеции равны между собой (a = b). |
| 2. | Диагонали трапеции равны между собой (d₁ = d₂). |
| 3. | Сумма углов при основаниях трапеции равна 180°: А+В = 180°. |
| 4. | Углы при основаниях трапеции смежны и дополнительны (А+С = 180°, В+D = 180°). |
| 5. | Высота трапеции – это отрезок, проведенный перпендикулярно между основаниями и соединяющий их середины. Высота трапеции обозначается как h. |
Знание свойств оснований трапеции позволяет проводить различные геометрические вычисления и находить неизвестные значения сторон, углов и высоты данной фигуры.
Высота трапеции

Свойства высоты трапеции:
- Высота трапеции делит ее на два треугольника, которые являются подобными друг другу и подобны всей трапеции.
- Высота трапеции является кратчайшим путем между ее основаниями, то есть сумма длин отрезаний, соединяющих вершины непарных сторон трапеции, меньше суммы длин отрезклв, соединяющих вершины парных сторон.
- Высота трапеции равна разности площадей двух треугольников, на которые она делит трапецию.
- Высота трапеции можно найти, зная длину одного из оснований, а также площадь трапеции.
Периметр трапеции
Обозначим длину первого основания трапеции как a, а длину второго основания трапеции - как b. Длину боковых сторон трапеции обозначим как c и d.
Тогда формула для вычисления периметра трапеции будет следующей:
Периметр = a + b + c + d
Таким образом, чтобы найти периметр трапеции, необходимо сложить длины всех ее сторон.
Знание периметра трапеции может быть полезным при решении различных задач, связанных с поиском и описанием данной фигуры.
Площадь трапеции
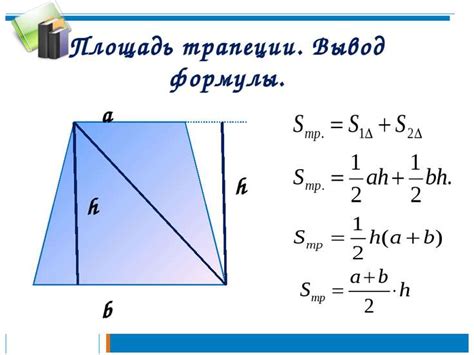
Площадь трапеции вычисляется по формуле:
S = (a + b) * h / 2
где:
- S - площадь трапеции;
- a и b - длины оснований трапеции;
- h - высота трапеции.
Чтобы найти площадь трапеции, необходимо знать длины ее оснований и высоту. Основаниями трапеции являются ее параллельные стороны, а высотой - отрезок, проведенный между основаниями поперек трапеции. Формула позволяет найти площадь трапеции, используя только эти три значения.
Площадь трапеции может быть выражена в квадратных единицах, так как это мера площади. Величина площади зависит от длин оснований и высоты трапеции.
Важно помнить, что длины оснований и высота должны быть измерены в одной системе измерения, например, в метрах или в сантиметрах, чтобы получить корректный результат.
Трапеция в геометрических построениях

С помощью трапеции можно выполнять различные геометрические построения. Например:
- Построение средней линии трапеции. Средняя линия трапеции - это отрезок, соединяющий середины ее непараллельных сторон. Для построения средней линии необходимо провести диагонали трапеции и соединить точки их пересечения.
- Построение высоты трапеции. Высотой трапеции называется перпендикуляр, опущенный из вершины не параллельной стороны на противоположную параллельную сторону. Для построения высоты нужно опустить перпендикуляр из одной из вершин непараллельных сторон на противоположную сторону.
- Построение равнобокой трапеции. Равнобокой трапецией называется трапеция, у которой боковые стороны равны между собой. Для построения равнобокой трапеции нужно провести диагонали трапеции, точки их пересечения будут являться серединами боковых сторон.
Трапеция в геометрических построениях имеет множество свойств, которые помогают в решении различных задач. Знание этих свойств позволяет уверенно работать с трапециями и выполнять точные построения.
Примеры использования трапеции
1. Архитектура: В архитектуре трапеция может использоваться в дизайне здания или моста. Например, форма крыши или перегона может иметь форму трапеции.
2. Торговля и экономика: В экономике трапеция может использоваться для построения графиков или диаграмм. Трапеции могут представлять различные показатели или тренды в экономической деятельности.
3. Математика: В математике трапеция используется для решения задач по геометрии и нахождения площади фигуры. Также трапеция может использоваться для иллюстрации различных геометрических свойств и теорем.
4. Изобразительное искусство: В изобразительном искусстве трапеция может быть использована для создания абстрактных или геометрических композиций. Форма трапеции может придавать произведению особую динамику или симметрию.
5. Физика: В физике трапеция может использоваться для описания движения тела или формы некоторых объектов. Например, в физике могут использоваться трапеции для описания траектории движения автомобиля или планеты.
Трапеция - это универсальная геометрическая фигура, которая имеет много применений в различных областях. Изучение свойств и применения трапеции позволяет лучше понять и использовать эту фигуру в различных задачах и заданиях.



