Геометрия – это раздел математики, изучающий пространственные формы, положения и отношения между ними. В 7 классе, учебная программа предусматривает изучение базовых понятий и принципов геометрии, а именно – евклидовой геометрии. Это одна из наиболее распространенных форм геометрии, которая применяется в повседневной жизни.
Теория в геометрии 7 класс охватывает основные понятия, на которых строится весь дальнейший материал по геометрии. Это включает в себя такие понятия, как взаимное расположение прямых и плоскостей, основные элементы фигур (точки, прямые, плоскости), а также базовые формулы и теоремы, которые позволяют решать геометрические задачи.
Основная задача теории в геометрии 7 класс – научить учеников использовать геометрические инструменты для решения различных задач, а также формировать логическое мышление и способность анализировать пространственные отношения. Предмет геометрии является неотъемлемой частью школьной программы и имеет практическое применение как в науке, так и в повседневной жизни.
Теория в геометрии 7 класс: основные понятия и применение

Одним из первых понятий, осваиваемых в 7 классе, является понятие "точка". Точка – это основной элемент геометрической фигуры, не имеющий размеров. От точки можно провести прямую и построить различные фигуры.
Другим важным понятием является "отрезок". Отрезок – это часть прямой, ограниченная двумя точками. В геометрии 7 класса, ученики изучают методы измерения длины отрезка и учатся работать с отрезками на плоскости.
Треугольник – это фигура, образованная тремя отрезками, соединяющими три точки, не лежащие на одной прямой. В 7 классе ученики изучают свойства треугольников, такие как сумма углов треугольника, равенства сторон и углов, а также методы построения треугольников.
Важным понятием геометрии 7 класса является также "параллель". Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются. В школьном курсе геометрии ученики учатся определять параллельные прямые и проводить различные построения с параллельными прямыми.
Геометрия имеет множество применений не только в школьной программе, но и в повседневной жизни. Знакомство с основными понятиями геометрии помогает ученикам развивать логическое мышление, усваивать абстрактные понятия, а также решать разнообразные задачи из разных областей науки и техники.
Геометрические фигуры и основные понятия
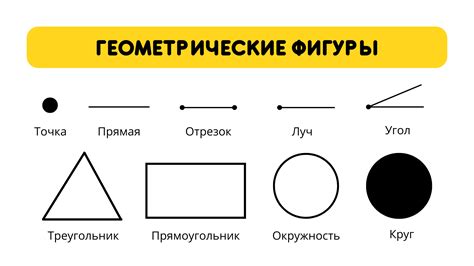
Многоугольник - это такая геометрическая фигура, у которой все стороны и углы равны или не все равны. Все многоугольники можно разделить на треугольники и четырехугольники. Существуют специальные треугольники - прямоугольник, равнобедренный и равносторонний треугольник.
Прямоугольник - это четырехугольник, у которого противоположные стороны параллельны и все углы прямые. Равнобедренный треугольник - это треугольник, у которого две стороны равны. Равносторонний треугольник - это треугольник, у которого все стороны равны и все углы равны 60 градусов.
Окружность - это множество всех точек плоскости, равноудаленных от одной фиксированной точки - центра окружности. Другие важные понятия связанные с окружностью - диаметр и радиус. Диаметр - это отрезок, соединяющий две точки на окружности через центр. Радиус - это отрезок, соединяющий центр окружности с любой точкой на окружности.
Таблица ниже представляет основные геометрические фигуры и их свойства:
| Фигура | Описание | Свойства |
|---|---|---|
| Треугольник | Многоугольник с тремя сторонами. | Сумма углов треугольника равна 180 градусам. |
| Прямоугольник | Четырехугольник с противоположными сторонами, параллельными и углами, равными 90 градусам. | Противоположные стороны равны и все углы прямые. |
| Ромб | Многоугольник с равными сторонами. | Противоположные углы равны и диагонали перпендикулярны. |
| Окружность | Множество точек равноудаленных от центра. | Диаметр равен удвоенному радиусу и сумма углов в центре равна 360 градусам. |
Это лишь некоторые из геометрических фигур и основных понятий, которые изучаются в геометрии 7 класса. Понимание этих понятий поможет учащимся развить пространственное мышление и решать задачи связанные с геометрией.
Понятие геометрической точки и ее свойства
Главное свойство геометрической точки - она может быть положена на бесконечно много различных мест на плоскости. Невозможно задать точное положение геометрической точки без использования других точек или координат.
С другой стороны, геометрическая точка может также рассматриваться как начальная точка при измерении расстояний или углов. Например, если нужно измерить расстояние между двумя точками, одна из точек может быть выбрана в качестве начальной точки.
У геометрической точки есть несколько свойств:
- Неделимость: Точку нельзя разделить на части, она не имеет ни объема, ни площади.
- Уникальность: Две разные точки не могут находиться в одном и том же месте на плоскости, каждая точка имеет свое уникальное положение.
- Бесконечность: Точка может быть помещена в любом месте на плоскости, она не имеет ограничений в положении.
Понимание геометрической точки и ее свойств является основным для понимания остальных геометрических понятий и построений в геометрии.
Геометрические линии и их классификация

Существует несколько основных типов геометрических линий:
- Прямая - это линия, которая не имеет начала или конца, она продолжается в бесконечность. Прямая также может быть описана как наиболее короткий путь между двумя точками.
- Луч - это линия, которая начинается с определенной точки и продолжается в одном направлении до бесконечности.
- Отрезок - это часть прямой линии, ограниченная двумя конечными точками.
- Кривая - это линия, которая может изменять свое направление между точками и не может быть прямой.
- Плоская кривая - это кривая, которая лежит на одной плоскости без изгибов.
Классификация геометрических линий помогает лучше понять их особенности и использование в геометрии. Она также позволяет создавать точные определения и применять их в решении геометрических задач.
Углы и их виды в геометрии
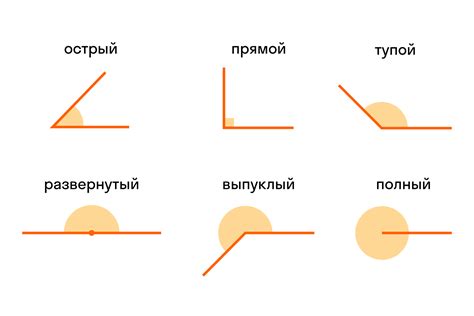
В геометрии существуют различные виды углов, каждый из которых имеет свои особенности. Рассмотрим основные виды углов:
| Название | Описание |
|---|---|
| Прямой угол | Угол, равный 90 градусам или четверти полного оборота. Лучи прямого угла образуют прямую линию. |
| Острый угол | Угол, меньший 90 градусов. Лучи острого угла направлены внутрь фигуры, при этом вершина находится между лучами. |
| Тупой угол | Угол, больший 90 градусов. Лучи тупого угла направлены наружу фигуры, при этом вершина также находится между лучами. |
| Прямоугольник | Угол, равный 90 градусам. Более узкое понятие прямого угла, встречающееся в основном при рассмотрении прямоугольных фигур. |
| Вертикальные углы | Углы, которые имеют общую вершину и расположены по разные стороны плоскости. Вертикальные углы равны друг другу. |
| Смежные углы | Углы, которые имеют общую вершину и общую сторону. Сумма смежных углов составляет 180 градусов. |
Знание различных видов углов в геометрии позволяет разбираться в основных понятиях и применять их для решения задач на построение и измерение углов.
Треугольники: классификация и основные свойства

Треугольники могут быть классифицированы по различным признакам:
По длинам сторон:
- Равнобедренный треугольник - имеет две равные стороны.
- Равносторонний треугольник - все стороны равны друг другу.
- Разносторонний треугольник - все стороны имеют разную длину.
По величине углов:
- Остроугольный треугольник - все углы острые (меньше 90 градусов).
- Прямоугольный треугольник - один из углов равен 90 градусам.
- Тупоугольный треугольник - один из углов больше 90 градусов.
Треугольники также имеют ряд основных свойств:
- Сумма углов треугольника равна 180 градусам. Угол в сумме с двумя другими углами треугольника составляет 180 градусов. Это свойство называется "основной суммой углов треугольника".
- Длина каждой стороны треугольника меньше суммы длин двух других сторон. Например, длина стороны AB меньше суммы длин сторон BC и AC. Это свойство называется "неравенством треугольника".
- Высота треугольника - это перпендикуляр, опущенный из вершины треугольника до основания (противоположной стороны). Высота может лежать как внутри треугольника, так и на продолжении одной из его сторон.
- Медиана треугольника - это отрезок, соединяющий вершину треугольника и середину противоположной стороны. Треугольник имеет три медианы, которые пересекаются в одной точке.
Ознакомление с классификацией треугольников и их основными свойствами позволяет более глубоко изучать геометрию и решать различные задачи, связанные с этой геометрической фигурой.
Четырехугольники и их классификация
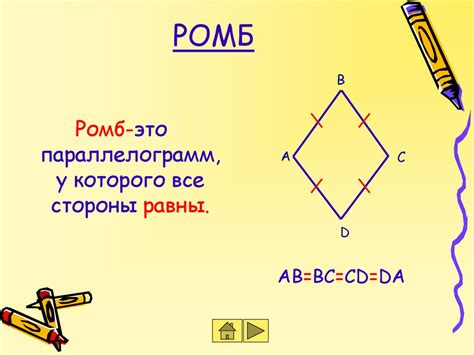
Самым простым видом четырехугольника является выпуклый четырехугольник. У него все углы меньше 180 градусов, а стороны не пересекаются. Примерами выпуклых четырехугольников являются прямоугольник, ромб, параллелограмм и трапеция.
Другим видом четырехугольников являются невыпуклые или вогнутые четырехугольники. Они имеют углы, большие 180 градусов, и одну или несколько сторон, которые пересекаются. Примеры вогнутых четырехугольников включают в себя некоторые виды квадратов и ромбов с вогнутыми углами.
Еще одной группой четырехугольников являются равносторонние четырехугольники. У них все стороны равны друг другу. Примерами таких фигур являются квадрат и ромб.
Также существуют прямоугольники, у которых все углы прямые, а стороны могут быть разными по длине. Трапеции имеют одну пару параллельных сторон.
Изучение четырехугольников и их классификация играют важную роль в геометрии. Они помогают нам понять и анализировать формы и свойства различных фигур, что может быть полезно в различных областях, таких как архитектура, дизайн и инженерное дело.
Площади и периметры геометрических фигур
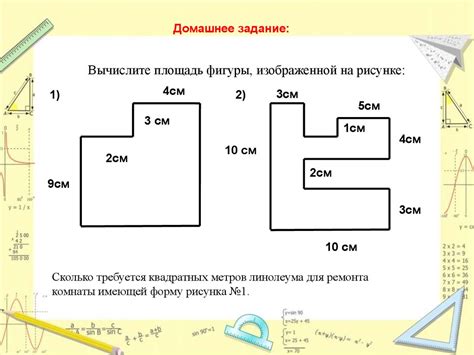
Площадь - это мера поверхности фигуры, выраженная числом. Вычисление площади различных фигур основано на формулах, которые зависят от их типа. Например, если мы хотим найти площадь прямоугольника, мы можем использовать формулу: площадь = длина × ширина.
Периметр - это длина контура фигуры, то есть сумма длин всех ее сторон. У разных фигур периметры рассчитываются по-разному. Например, для прямоугольника периметр рассчитывается по формуле: периметр = 2 × (длина + ширина).
Знание площадей и периметров геометрических фигур позволяет решать различные задачи. Например, с помощью этих понятий мы можем определить, сколько плиток нужно для выложения пола или стены, или найти площадь участка земли для строительства дома.
Важно уметь применять понятия площади и периметра в реальных ситуациях. Это поможет не только в решении задач, но и в анализе и понимании окружающего мира. Знание геометрии и основных понятий, таких как площадь и периметр фигур, является важной составляющей образования и развития человека.
Понятие симметрии и основные примеры
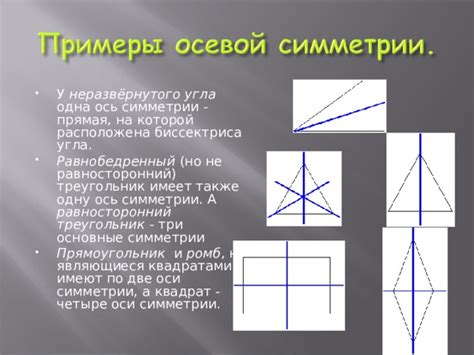
В геометрии выделяют несколько типов симметрии:
| Тип симметрии | Описание | Примеры |
|---|---|---|
| Осевая симметрия | Фигура симметрична относительно оси, то есть ее половинки отображаются друг в друга. | Прямоугольник, квадрат |
| Плоскостная симметрия | Фигура симметрична относительно плоскости, то есть ее зеркальные отображения совмещаются. | Круг, треугольник |
| Центральная симметрия | Фигура симметрична относительно центра, то есть ее точки симметричны относительно центральной точки. | Окружность |
Эти типы симметрии могут использоваться для решения различных задач в геометрии. Например, осевая симметрия позволяет находить симметричные точки и линии относительно заданной оси. Плоскостная и центральная симметрия могут использоваться для построения фигур и нахождения симметричных элементов.
Применение геометрии в повседневной жизни

- Архитектура: Геометрия играет ключевую роль в создании архитектурных проектов. Архитекторы используют принципы геометрии для расчета пропорций зданий, создания равномерных фасадов и определения гармоничного соотношения деталей.
- Конструирование: Геометрия помогает инженерам и конструкторам создавать различные объекты, начиная от простых машин и аппаратов до сложных сооружений. Использование геометрии позволяет оптимизировать форму и структуру объекта с целью достижения максимальной прочности и эффективности работы.
- Навигация и картография: Геометрические принципы используются при разработке карт и навигационных систем. Они позволяют определить местоположение объектов на карте, проложить оптимальный маршрут и рассчитать расстояние между точками.
- Дизайн: Геометрия имеет большое значение в сфере дизайна. Дизайнеры используют геометрические формы и пропорции для создания эстетически привлекательных и гармоничных композиций.
- Медицина: Геометрия применяется в медицине при планировании хирургических операций и подгонке протезов. Врачи и инженеры используют геометрические модели для создания точной копии части тела или определения оптимального расположения имплантата в организме пациента.
Применение геометрии в повседневной жизни свидетельствует о том, что эта наука не только теоретическая, но и практическая, помогающая нам в различных сферах деятельности.



