Скорость – одно из важнейших понятий в математике, которое изучается уже в 4 классе. Это понятие помогает нам понять, насколько быстро или медленно что-то движется или меняется. Скорость – это отношение пройденного пути или изменения к затраченному времени. Она позволяет нам количественно оценить, насколько быстро или медленно происходит то или иное явление.
В математике скорость изображается символом v. А чтобы вычислить скорость, необходимо знать два параметра: пройденный путь (s) и затраченное время (t). Формула для вычисления скорости выглядит так: v = s / t. Эта формула позволяет нам определить, сколько единиц пути мы проходим или изменяем за единицу времени. Например, если мы проходим 5 километров за 1 час, то наша скорость будет равна 5 километров в час.
Важно понимать, что скорость может быть как положительной, так и отрицательной. Положительная скорость означает движение вперед или увеличение параметра, а отрицательная скорость – движение назад или уменьшение параметра. Например, если при понижении температуры воздуха зимой на 3 градуса за 1 час, скорость будет равна -3 градуса в час.
Скорость в математике 4 класс
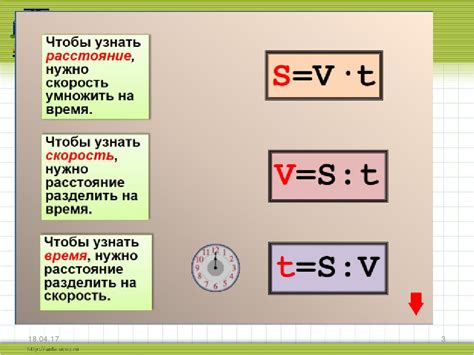
Для того чтобы рассчитать скорость, нужно знать расстояние, которое объект преодолел, и время, за которое он это сделал. Формула для определения скорости проста: скорость = расстояние / время.
Важно понять, что скорость может быть разной в зависимости от времени и расстояния. Например, если объект перемещается со скоростью 10 километров в час, он преодолеет 20 километров за 2 часа. Но если он будет двигаться с такой же скоростью, но только в течение 1 часа, он преодолеет только 10 километров.
Скорость также может быть положительной или отрицательной, в зависимости от направления движения. Если объект движется вперед, скорость будет положительной. Если он движется назад, скорость будет отрицательной.
В математике 4 класса скорость является важным понятием при изучении геометрии и алгебры. Она помогает понять, как движутся объекты и как изменяется их положение в пространстве со временем.
Концепция скорости

Предметно-пространственная скорость – это пример того, когда измеряется скорость движения тела или объекта в определенном пространстве (например, сантиметрах, метрах или километрах в секунду).
Временная скорость – это величина, которая показывает, какое расстояние тело проходит за фиксированный период времени (например, за секунду, минуту или час).
В математике скорость обычно обозначается буквой 'v' и измеряется в единицах, соответствующих пространственным размерностям (например, м/с).
Для расчета скорости используется следующая формула:
v = s / t
где v – скорость, s – пройденное расстояние, t – затраченное время.
Зная значения пройденного расстояния и затраченного времени, можно рассчитать скорость объекта. Например, если автомобиль проехал 100 километров за 2 часа, то его скорость будет 50 км/ч.
Понимание концепции скорости помогает ученикам лучше понять и описывать движение объектов и решать простые задачи в математике и физике.
Измерение скорости

Измерение скорости происходит с помощью различных инструментов и методов. Один из таких методов – использование специального прибора, называемого скорометром. Скорометр позволяет измерить скорость движения объекта в определенный момент времени.
Другой метод измерения скорости – использование формулы, в которой скорость вычисляется как отношение пройденного расстояния к затраченному времени. Формула выглядит следующим образом: скорость = пройденное расстояние / затраченное время.
Для того чтобы измерить скорость, необходимы точные измерения времени и расстояния. Время можно измерить с помощью секундомера или часов, а расстояние – с помощью измерительной ленты или других инструментов.
В математике 4 класса изучаются простые задачи на вычисление скорости. Решая такие задачи, ученикам необходимо определить пройденное расстояние и затраченное время, а затем вычислить скорость. Это помогает развить навык работы с числами и понимание основных понятий физики в контексте математики.
Связь скорости с расстоянием и временем

Чтобы вычислить скорость, необходимо знать пройденное расстояние и время, затраченное на это расстояние. Формула для вычисления скорости выглядит следующим образом:
Скорость = Расстояние / Время
Например, если автомобиль проехал 100 километров за 2 часа, то его скорость будет равна 100 / 2 = 50 километров в час.
Также можно использовать эту формулу для нахождения расстояния или времени. Например, если известна скорость и время, можно найти расстояние, пройденное объектом. Для этого необходимо умножить скорость на время:
Расстояние = Скорость * Время
Кроме того, можно выразить время через расстояние и скорость:
Время = Расстояние / Скорость
Знание связи между скоростью, расстоянием и временем позволяет решать различные задачи в математике, связанные с движением и перемещением объектов.
Скорость как отношение расстояния и времени

Для вычисления скорости необходимо знать два параметра: расстояние, пройденное объектом, и время, затраченное на это перемещение. Скорость вычисляется путем деления расстояния на время:
Скорость = Расстояние / Время
Например, если автомобиль проехал 200 километров за 2 часа, то его скорость равна 200/2 = 100 километров в час.
Скорость может быть разной в зависимости от условий движения. Например, при движении по трассе автомобиль может развивать более высокую скорость, чем при движении по городским улицам с ограничениями скорости.
Понимание понятия скорости помогает понять, как быстро или медленно объект движется, а также влияет на решение разнообразных задач, связанных с перемещением.
Графическое представление скорости
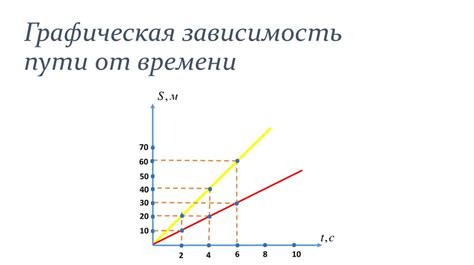
Графическое представление скорости может помочь нам лучше понять, как движется объект. Для этого мы можем построить график, на котором по оси X откладывается время, а по оси Y - расстояние, которое пройдет объект за это время.
Если объект движется с постоянной скоростью, то график будет прямой линией с постоянным наклоном. Если скорость увеличивается, то линия будет иметь положительный наклон, а если скорость уменьшается, то линия будет иметь отрицательный наклон.
При анализе графика скорости можно определить такие характеристики движения, как скорость на начальном и конечном отрезках, равномерность движения, промежуток времени, за который объект изменяет скорость и другие.
Расчет скорости по формуле

Для расчета скорости необходимо знать пройденное расстояние и время, затраченное на его преодоление. Формула для расчета скорости выглядит следующим образом:
Скорость (V) = расстояние (S) / время (t)
Скорость измеряется в единицах длины на единицу времени, например, метры в секунду или километры в час. При расчете необходимо учесть, что расстояние и время должны иметь одни и те же единицы измерения.
Например, если автомобиль проехал расстояние 200 километров за 4 часа, то скорость будет равна 200 км / 4 ч = 50 км/ч. Это означает, что автомобиль двигался со скоростью 50 километров в час.
Кроме того, при расчете скорости необходимо учитывать направление движения. Если оно известно, то скорость можно представить вектором, указывающим на направление и величину скорости.
Источник: учебник по математике для 4 класса
Примеры задач на скорость

Ниже приведены несколько примеров задач на расчет скорости:
| Пример | Условие задачи | Решение |
|---|---|---|
| Пример 1 | Аня прошла 400 метров за 1 минуту. Найдите ее скорость в метрах в секунду. | Скорость вычисляется по формуле: скорость = расстояние / время. В данном случае, скорость = 400 м / 60 с = 6.67 м/с. |
| Пример 2 | Вова проехал на велосипеде 5 километров за 10 минут. Найдите его скорость в метрах в секунду. | Сначала нужно перевести расстояние из километров в метры: 5 км = 5000 м. Затем применим формулу скорости: скорость = 5000 м / 600 с = 8.33 м/с. |
| Пример 3 | Мальчик бежит со скоростью 4 метра в секунду. За какое время он пробежит 200 метров? | Подставим известные значения в формулу расчета времени: время = расстояние / скорость. Получим время = 200 м / 4 м/с = 50 секунд. |
Это лишь некоторые примеры задач, связанные со скоростью. В математике существует множество других задач и концепций, связанных с этой темой.
Задачи с переменной скоростью
При решении задач с переменной скоростью необходимо учитывать, что скорость может меняться в зависимости от времени или от других факторов. Рассмотрим несколько примеров таких задач.
Пример 1:
Автомобиль движется со скоростью 60 км/ч. Через 2 часа после начала движения скорость увеличивается до 80 км/ч. Какое расстояние пройдет автомобиль за 3 часа после начала движения?
Решение:
За первые 2 часа автомобиль проедет расстояние, равное произведению его начальной скорости на время движения: 60 км/ч * 2 ч = 120 км.
За следующие 3 часа автомобиль будет двигаться со скоростью 80 км/ч. Расстояние, пройденное за это время, равно произведению новой скорости на время движения: 80 км/ч * 3 ч = 240 км.
Итого, за 3 часа после начала движения автомобиль пройдет 120 км + 240 км = 360 км.
Пример 2:
Поезд движется со скоростью 100 км/ч. Через каждый час после начала движения его скорость увеличивается на 20 км/ч. Через сколько часов поезд достигнет скорости 160 км/ч?
Решение:
За первый час поезд проедет расстояние, равное его начальной скорости: 100 км/ч.
За второй час его скорость будет 100 км/ч + 20 км/ч = 120 км/ч, и поезд проедет еще 120 км.
За третий час его скорость будет 120 км/ч + 20 км/ч = 140 км/ч, и поезд проедет еще 140 км.
За четвертый час его скорость будет 140 км/ч + 20 км/ч = 160 км/ч, и поезд достигнет желаемой скорости.
Итого, поезд достигнет скорости 160 км/ч через 4 часа после начала движения.
Практическое применение скорости в жизни

Дорожное движение: скорость – основной параметр, определяющий время, за которое автомобиль достигнет своего пункта назначения. Знание скорости помогает оценить необходимое время на поездку и спланировать свой маршрут.
Спорт: скорость имеет огромное значение в различных видах спорта, например, в беге, плавании или велоспорте. Знание своей скорости помогает спортсменам улучшить свои результаты и достичь новых спортивных высот.
Экономика: скорость является ключевым фактором в экономической деятельности и транспортной логистике. Быстрая доставка товаров и услуг влияет на эффективность бизнеса и удовлетворение потребностей клиентов.
Наука и технологии: скорость используется во многих научных исследованиях и разработках. Например, в физике для изучения движения тел или в компьютерной графике для создания реалистичных анимаций.
Это только небольшая часть областей, где скорость играет важную роль. В повседневной жизни мы постоянно сталкиваемся с понятием скорости и используем его для принятия решений и планирования своих действий.



