Си (синус) – одна из основных тригонометрических функций, широко применяемая в физике для вычисления различных величин. Определение синуса – отношение противолежащего катета к гипотенузе прямоугольного треугольника. В физических расчетах синус используется для решения задач, связанных с колебаниями, волнами, периодическими процессами и другими явлениями.
Существует несколько способов вычисления значения синуса:
1. Геометрический подход: построение треугольника, нахождение противолежащего катета и гипотенузы, вычисление отношения. Этот способ применяется при решении прямоугольных треугольников и геометрических задач.
2. Ряд Тейлора: разложение синуса в бесконечную сумму, каждое слагаемое которой можно посчитать при помощи факториалов, степеней и синусов. Ряд Тейлора позволяет приближенно вычислить значение синуса с заданной точностью.
3. Тригонометрическая окружность: построение специальной окружности с радиусом 1, нахождение координаты точки пересечения радиуса с определенным углом и определение значения синуса как ординаты этой точки. Этот способ особенно эффективен при использовании компьютерных программ и таблиц.
Си – одна из самых важных функций в физике. Знание определения синуса и способов его вычисления позволяет проводить более точные и эффективные расчеты в физических задачах.
Что такое Си в физике?
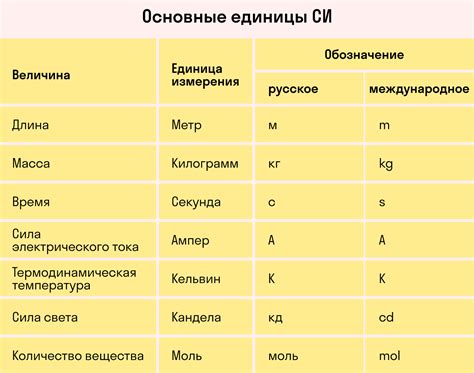
Си включает в себя семь основных единиц: метр (длина), килограмм (масса), секунда (время), ампер (сила тока), кельвин (температура), мол (количество вещества) и кандела (сила света).
В Си существуют также производные единицы, которые можно выразить через основные единицы. Например, скорость можно измерять в метрах в секунду, сила - в ньютонах, энергия - в джоулях и так далее.
Си обеспечивает единое и универсальное понимание физических величин и их измерений. Это позволяет ученым, инженерам и другим специалистам работать с одними и теми же единицами, что делает обмен данными и результатами исследований гораздо проще и эффективнее.
Зачем нужно вычислять Си?

Период колебаний осциллирующей системы, измеренный в единицах времени, называется циклической частотой или частотой колебаний. Си (или именно циклическая частота) играет важную роль в физике при изучении колебательных и волновых процессов, таких как механические колебания, электрические колебания и световые волны.
Вычисление Си позволяет определить, сколько колебаний или волн происходит в единицу времени. Это позволяет нам более точно описывать и предсказывать поведение колебательных и волновых систем. Например, зная циклическую частоту электрических колебаний в цепи, можно рассчитать время между повторениями сигнала или определить максимальные значения напряжения и тока.
Вычисление Си также позволяет сравнивать и анализировать различные системы колебаний и волн и находить общие закономерности между ними. Это помогает установить связи и улучшить понимание физических явлений.
Кроме того, знание Си и его вычисление являются неотъемлемой частью физических вычислений и моделирования. Циклическая частота используется в уравнениях и формулах для расчета различных физических параметров и свойств систем.
Таким образом, вычисление Си является важной задачей в физике, которая позволяет более полно и точно описывать и изучать колебательные и волновые процессы, а также использовать их в практических приложениях.
Определение

Си является производной единицей исходной системы единиц СГС. В системе СИ, си равен единице проводимости в метре квадрате на Ом (1 С = 1 м²/Ом).
Си обозначается буквой С и может использоваться для измерения проводимости материалов, таких как металлы, полупроводники и электролиты. Чем выше значение электрической проводимости, тем легче электрический ток протекает через материал.
Способы вычисления си включают измерение сопротивления материала и расчет проводимости по формуле C = 1/R, где R - сопротивление материала.
Си является основным понятием в электросвязи и электронике, и его понимание важно для понимания основ электрических цепей и электронных компонентов.
Основные составляющие Си
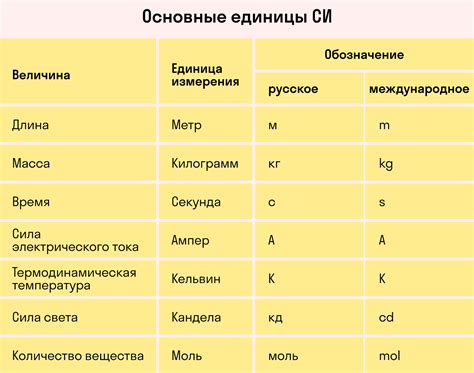
Основные составляющие СИ включают:
| Единица | Обозначение | Описание |
|---|---|---|
| Метр | m | Единица длины, используемая для измерения пространства. |
| Килограмм | kg | Единица массы, используемая для измерения количества вещества. |
| Секунда | s | Единица времени, используемая для измерения процессов и событий. |
| Ампер | A | Единица электрического тока, используемая для измерения электрической силы. |
| Кельвин | K | Единица температуры, используемая для измерения холода и тепла. |
| Кандела | cd | Единица светового потока, используемая для измерения яркости света. |
| Моль | mol | Единица вещества, используемая для измерения количества частиц. |
Эти основные единицы образуют основу для всех физических измерений и являются основными стандартами, на которых основана вся СИ.
Принципы вычисления Си

Для вычисления силы тока (Си) в физике существуют несколько основных принципов:
Закон Ома является основным принципом, на основе которого можно вычислить силу тока в электрической цепи. Согласно Закону Ома, сила тока пропорциональна напряжению и обратно пропорциональна сопротивлению в цепи. Формула для вычисления тока по Закону Ома выглядит следующим образом:
I = V / R, где I представляет силу тока, V - напряжение в цепи, R - сопротивление в цепи.
Закон Кирхгофа также применяется для вычисления силы тока. Закон Кирхгофа состоит из двух основных принципов - сумма токов, входящих в узел, равна сумме токов, выходящих из узла, а сумма падений напряжения в замкнутом контуре равна сумме электродвижущих сил в этом контуре. С помощью Закона Кирхгофа можно вычислить силу тока на различных участках цепи.
Метод Кирхгофа - это метод, основанный на Законе Кирхгофа, позволяющий вычислить силу тока в сложных цепях. Метод Кирхгофа заключается в составлении уравнений, их решении и нахождении неизвестных токов в цепи.
Силомеры и амперметры также позволяют вычислить силу тока. Силомеры - это специальные измерительные приборы, предназначенные для измерения силы тока в электрической цепи. Амперметры - это приборы, которые вставляются в цепь для измерения силы тока. Оба этих прибора основаны на физических принципах, позволяющих вычислить силу тока по показаниям прибора.
Таким образом, в физике существует несколько принципов и методов вычисления силы тока, которые позволяют определить его значение в различных электрических цепях.
Способы вычисления

В физике существует несколько основных способов вычисления физических величин с использованием языка программирования Си. Некоторые из них включают:
- Использование математических формул. Формулы позволяют вычислять значения физических величин, основываясь на исходных данных и известных законах и связях. Для этого нужно знать соответствующую формулу и передать в нее необходимые значения переменных.
- Методы численного решения. В некоторых случаях вычисление физических величин может быть сложным или невозможным с использованием аналитических формул. В таких случаях можно применить методы численного решения, такие как метод Ньютона или метод Эйлера.
- Использование библиотек. Самостоятельное написание алгоритмов для решения сложных задач вычисления физических величин может быть трудным и затратным по времени. Поэтому можно использовать специализированные библиотеки, которые предоставляют готовые функции для вычисления определенных видов физических величин.
- Симуляция и моделирование. В некоторых случаях, для предсказания поведения физической системы или вычисления физических величин, можно использовать методы симуляции и моделирования. Симуляции позволяют создавать виртуальные модели объектов или систем и проводить вычисления на основе этих моделей.
Выбор способа вычисления зависит от поставленной задачи, доступных данных и требуемой точности результатов. Важно выбрать наиболее подходящий способ и правильно написать соответствующий код на языке Си.
Метод Джоуля-Томсона

Процесс Джоуля-Томсона происходит при потоке газа через пористую перегородку, называемую дросселем. При прохождении через дроссель, газ испытывает изменение давления и, как следствие, изменение температуры.
Суть этого метода заключается в измерении изменения температуры газа до и после прохождения через дроссель при постоянной температуре окружающей среды. Если газ охлаждается при прохождении через дроссель, то говорят о положительном эффекте Джоуля-Томсона. Если же газ нагревается, то говорят о отрицательном эффекте Джоуля-Томсона.
Метод Джоуля-Томсона широко применяется в физике и химии для измерения коэффициента Джоуля-Томсона, который характеризует способность газа охлаждаться или нагреваться при расширении или сжатии. Этот метод особенно полезен при исследовании свойств некоторых газов, например, при определении критической точки газа.
Измерение эффекта Джоуля-Томсона осуществляется с помощью специальных устройств, таких как Джоуля-Томсоновские клетки. Эти устройства позволяют контролировать процесс расширения или сжатия газа через дроссель и измерять изменение температуры газа.
Метод Джоуля-Томсона является важным инструментом для физиков и инженеров, которые работают с газами и требуют точных данных о их свойствах. Этот метод позволяет проводить эксперименты и получать значения термодинамических параметров газов, которые могут быть использованы для различных практических целей.
Метод изобарного расширения
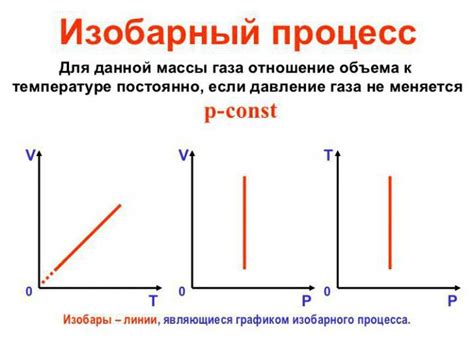
Для определения коэффициента теплового расширения газов методом изобарного расширения используется таблица Прадля. В ней представлены значения объема газа при различных температурах и постоянном давлении. Измерения проводятся при двух разных температурах, а затем с использованием формулы вычисляется коэффициент теплового расширения газа.
| Температура (°C) | Объем (л) |
|---|---|
| 20 | 2.5 |
| 30 | 3.0 |
Для вычисления коэффициента теплового расширения газа по методу изобарного расширения используется следующая формула:
γ = (V2 - V1) / (V1 * (T2 - T1))
Где γ - коэффициент теплового расширения газа, V1 и V2 - объем газа при первой и второй температуре соответственно, T1 и T2 - первая и вторая температуры.
При проведении измерений и вычислении коэффициента теплового расширения газа следует учитывать погрешности измерений и обеспечивать стандартные условия (например, комнатную температуру и атмосферное давление).
Метод расчета по производным

Для использования метода расчета по производным требуется знание математической модели, описывающей исследуемый процесс. Исходя из этой модели, можно вывести аналитическое выражение для производной функции и использовать его для расчета значений исследуемой величины.
Чтобы провести расчет по производным, необходимо знать значения физических величин, от которых зависит исследуемый процесс. Подсчитывая производные по этим величинам и затем подставляя значения в полученное аналитическое выражение для производной функции, можно получить значения исследуемой величины.
Основное преимущество метода расчета по производным заключается в том, что он позволяет получить значения величин, которые невозможно измерить прямым экспериментом. Также этот метод обладает высокой точностью расчетов в сравнении с другими методами.
Однако следует учитывать, что метод расчета по производным требует знания математической модели и навыков вычислительного анализа. Кроме того, точность расчетов может быть ограничена точностью измерения исходных данных.
Примеры вычисления Си
Вычисление скорости света (Си) может осуществляться различными способами в физике. Рассмотрим два примера:
- Метод Физического электромагнитного колебания - данный метод основан на измерении времени, за которое электромагнитное колебание распространяется от передатчика до приемника. Зная расстояние между ними и время задержки, можно вычислить скорость света по формуле: Си = Расстояние / Время.
- Опыты по интерференции - в этом методе используется явление интерференции света, которое происходит при взаимодействии двух или нескольких волн. Измеряется разность фаз между волнами и вычисляется длина волны света. С помощью соотношения Си = Длина волны * Частота можно определить скорость света.
Эти методы позволяют получить достаточно точные значения Си и являются основой для измерения скорости света в различных научных экспериментах.



