Равнобедренный треугольник - это геометрическая фигура, у которой две стороны и два угла равны друг другу. В греческом языке слово "равнобедренный" обозначает "равные ноги", что указывает на особенность этого треугольника - наличие двух равных сторон.
Одно из ключевых свойств равнобедренного треугольника - равенство углов при его основании. Также в равнобедренном треугольнике две равные стороны соответствуют двум равным углам, формирующимся на основании. Это нарушается только в случае равностороннего треугольника, где все стороны и углы равны между собой.
Равнобедренные треугольники могут быть использованы в различных областях, таких как архитектура, инженерия, графика и т.д. Благодаря своим геометрическим свойствам они позволяют решать разнообразные задачи, например, строить устойчивые и прочные конструкции.
Изучение равнобедренных треугольников важно для понимания основных понятий геометрии и формирования навыков аналитического мышления. Это также является важным средством для абстрактного мышления и развития логического и пространственного мышления. Поэтому знание свойств равнобедренных треугольников является не только академически значимым, но и полезным в повседневной жизни.
Определение равнобедренного треугольника
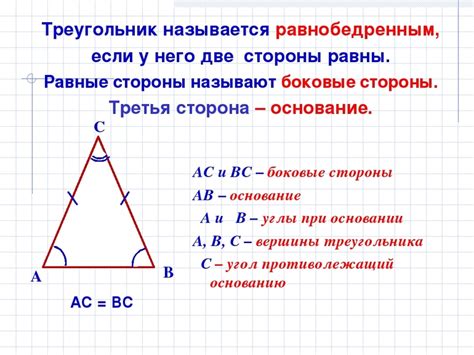
Для того чтобы определить, является ли треугольник равнобедренным, необходимо проверить равенство длин двух его сторон и равенство двух углов при основании.
Если две стороны треугольника равны по длине, то говорят, что треугольник имеет равные боковые стороны. Они также являются основаниями равнобедренного треугольника.
Равнобедренный треугольник является частным случаем треугольника, в котором все стороны и углы равны. Он отличается от равностороннего треугольника, у которого все стороны равны, но углы могут быть разными.
Таблица ниже показывает визуальное представление равнобедренного треугольника:
| Угол при вершине | ||||
| / | \ | |||
| / | – | – | \ | / |
| Основание |
Примеры равнобедренных треугольников: треугольник со сторонами 3, 4 и 3, треугольник со сторонами 5, 6 и 5.
Свойства равнобедренного треугольника
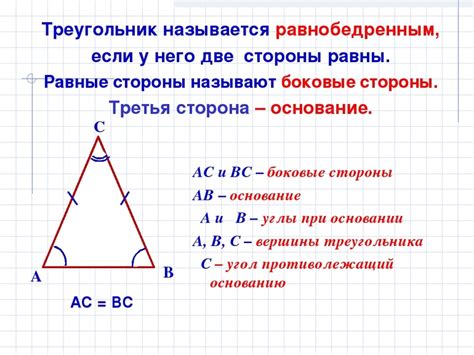
Главное свойство равнобедренного треугольника заключается в равенстве двух его боковых сторон. Это означает, что если две стороны треугольника равны между собой, то углы при основании также будут равны. В равнобедренном треугольнике сторона, прилегающая к углу, равному углу при основании, называется боковой стороной, а сторона, противолежащая этому углу, – основанием.
Кроме того, равнобедренный треугольник обладает рядом других свойств:
- Перпендикуляр из вершины, противолежащей основанию, опущенный на основание, является высотой треугольника и делит его на два равных прямоугольных треугольника.
- Серединный перпендикуляр к основанию равнобедренного треугольника проходит через вершину, противолежащую этому основанию, и делит его на два равных прямоугольных треугольника.
- Биссектриса, проведенная из вершины, противолежащей основанию, делит угол при основании на два равных угла, а основание – на две равные части.
- Медиана, проведенная из вершины, противолежащей основанию, делит предполагаемую основу треугольника на две равные части.
Формулы для вычисления площади и периметра равнобедренного треугольника
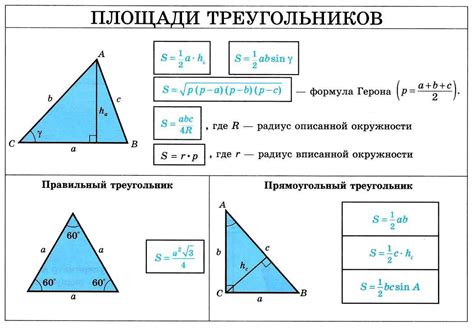
Площадь и периметр равнобедренного треугольника можно вычислить с помощью следующих формул:
1. Площадь равнобедренного треугольника.
Площадь равнобедренного треугольника может быть вычислена по формуле:
S = (a^2 * h)/2,
где a - длина основания треугольника, h - высота, опущенная на основание.
2. Периметр равнобедренного треугольника.
Периметр равнобедренного треугольника можно вычислить по формуле:
P = 2a + b,
где a - длина равных сторон треугольника, b - длина основания треугольника.
Эти формулы позволяют находить площадь и периметр равнобедренного треугольника при известных значениях его основания и высоты, а также при известной длине сторон.
Углы равнобедренного треугольника

- Базисы равнобедренного треугольника равны, поэтому углы при основании равнобедренного треугольника равны между собой. Они называются основными углами равнобедренного треугольника.
- Угол между боковой стороной и основанием равнобедренного треугольника называется вершинным углом равнобедренного треугольника.
- Вершинные углы равнобедренного треугольника равны между собой. Это означает, что противолежащие им стороны также равны.
- Основные углы равнобедренного треугольника равны и образуют вместе вершинный угол.
- Сумма всех углов равнобедренного треугольника равна 180 градусам.
Как найти длину биссектрисы равнобедренного треугольника
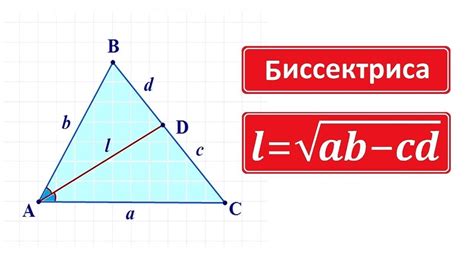
Длина биссектрисы равнобедренного треугольника может быть найдена с использованием формулы, основанной на свойствах данного вида треугольника.
1. Найдите длину основания равнобедренного треугольника. Основание - это одна из сторон треугольника, которая не является равной другим двум сторонам. Обозначим основание как a, а равные стороны – как b.
2. Используя основание и формулу для нахождения площади треугольника, можно найти высоту треугольника. Площадь треугольника равна половине произведения длины основания на высоту. Поэтому высота треугольника h будет равна (2 * площадь) / a.
3. Так как в равнобедренном треугольнике биссектриса является перпендикуляром к основанию и к одной из равных сторон, то можно использовать теорему Пифагора для нахождения длины биссектрисы (b/2)^2 = h^2 + (a/2)^2.
4. Наконец, найдите длину биссектрисы треугольника, извлекая квадратный корень из обеих сторон последнего уравнения. Таким образом, длина биссектрисы равной стороны треугольника будет равна корню из [(a/2)^2 + h^2].
Применяя эти шаги, вы сможете найти длину биссектрисы равнобедренного треугольника и использовать ее для решения различных геометрических задач.
Примеры задач:

1. Найдите площадь равнобедренного треугольника со сторонами длиной 5 см, основание которого равно 6 см.
2. Известно, что в равнобедренном треугольнике один из углов при основании равен 60 градусов. Найдите острый угол этого треугольника.
3. В равнобедренном треугольнике перпендикуляр, опущенный из вершины на основание, равен 6 см, а основание – 8 см. Найдите площадь треугольника.
4. Сторона равнобедренного треугольника равна 10 см. Найдите радиус вписанной окружности.
5. В равнобедренном треугольнике сторона равна 12 см, а высота, опущенная на основание, равна 9 см. Найдите площадь треугольника.
Применение равнобедренного треугольника в практике
Одним из самых распространенных применений равнобедренных треугольников является строительство и архитектура. Равнобедренные треугольники часто используются для создания устойчивых и прочных конструкций, таких как крыши, окна и арки. Благодаря своей симметрии и устойчивости равнобедренные треугольники позволяют создавать эстетически привлекательные и прочные строительные элементы.
Еще одно практическое применение равнобедренных треугольников можно найти в геодезии и навигации. С помощью равнобедренных треугольников можно измерять расстояния, высоты и углы на местности. Это особенно полезно в навигации и создании карт, так как равнобедренные треугольники позволяют точно определить местоположение и ориентацию объектов.
Равнобедренные треугольники также используются в физике и инженерии. Например, они применяются в расчетах силы или давления, так как равнобедренные треугольники имеют одинаковые углы и длину боковых сторон, что упрощает математические вычисления.
Кроме того, равнобедренные треугольники играют важную роль в геометрии и математике. Они являются основой для изучения других типов треугольников и могут использоваться в доказательствах различных геометрических теорем.
| Применение | Пример |
|---|---|
| Строительство и архитектура | Равнобедренные треугольники используются для создания прочных и устойчивых конструкций. |
| Геодезия и навигация | Равнобедренные треугольники помогают определять местоположение и ориентацию объектов на местности. |
| Физика и инженерия | Равнобедренные треугольники используются для расчетов силы или давления. |
| Геометрия и математика | Равнобедренные треугольники являются основой для изучения других типов треугольников и доказательства геометрических теорем. |



