В геометрии 7 класса одной из важных тем является изучение противоположных лучей. Это понятие играет важную роль в построении аксиоматической теории геометрии. Противоположные лучи - это довольно интересное и полезное понятие, которое помогает понять, как работает геометрическое пространство.
Противоположные лучи - это два луча, которые имеют одну общую начальную точку и направлены в разные стороны. Отличительной особенностью противоположных лучей является то, что они не пересекаются и не имеют других общих точек, кроме начальной.
Противоположные лучи можно представить себе как две стрелки, которые начинают своё движение из одного и того же места, но направлены в противоположные стороны. Например, если взять точку A и провести из неё два луча - AB и AC, то они будут являться противоположными, так как имеют общую начальную точку A, но направлены в противоположные стороны - вдоль отрезков AB и AC.
Противоположные лучи: понятие и основные свойства
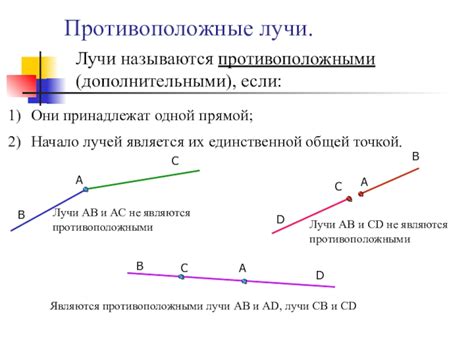
Основные свойства противоположных лучей:
- Начало: Оба луча начинаются в одной точке, которая называется началом лучей. Эта точка задаётся общей вершиной двух прямых.
- Направление: Противоположные лучи направлены в разные стороны. Один луч продолжается вправо от вершины, а другой – влево.
- Бесконечность: Прямые линии, на которых лежат противоположные лучи, продолжаются в обе стороны бесконечно.
- Угол: Противоположные лучи образуют угол, который равен 180 градусам или пи радианам. Этот угол называется прямым.
Противоположные лучи широко используются в геометрии и математике для изучения свойств прямых линий и углов. Они помогают определить различные типы углов и проверять параллельность прямых. Кроме того, понимание противоположных лучей важно при решении задач на построение и доказательство теорем.
Что такое геометрия и зачем она нужна?
Геометрия помогает нам понять формы и структуры нашей окружающей среды. Она используется в архитектуре, инженерии, дизайне и других областях для создания и анализа трёхмерных моделей и построения различных сооружений.
Она также играет важную роль в технике и технологии. Геометрические принципы используются в разработке компьютерных графических систем, виртуальной реальности и трёхмерной печати.
Геометрические понятия и методы применяются в физике, чтобы описать движение тел и взаимодействие частиц. Они также используются в экономике и статистике для анализа данных и моделирования различных ситуаций.
Геометрия развивает наше абстрактное и логическое мышление, улучшает наши навыки решения проблем и развивает наше воображение. Она помогает нам лучше понимать мир вокруг нас и находить элегантные решения для различных задач.
Таким образом, геометрия является неотъемлемой частью нашей жизни и имеет широкий спектр применений в различных областях знания и деятельности.
Разделение лучей: основные понятия и определения

Противоположные лучи – это два луча, которые имеют общий начальный пункт и противоположные направления. Другими словами, они расположены на одной прямой, начиная из одной точки, но направлены в противоположные стороны.
Чтобы лучи были противоположными, они должны иметь одну и ту же длину, но направлены в противоположные стороны друг относительно общего начального пункта.
Противоположные лучи могут быть использованы для определения, например, угла или прямой линии. Они также широко применяются для решения геометрических задач и конструкций.
Понимание основных понятий и определений, связанных с разделением лучей, является важным для изучения геометрии и решения задач, связанных с пространством и формами.
Что означает понятие "противоположные лучи"?

Противоположные лучи – это два луча, исходящие из одной точки и направленные в противоположных направлениях. Точка, из которой эти лучи исходят, называется вершиной противоположных лучей.
Основными свойствами противоположных лучей являются:
- Противоположные лучи имеют одинаковую начальную точку (вершину) и разные направления;
- При продолжении противоположных лучей они никогда не пересекаются;
- Противоположные лучи могут быть равными, если они находятся на одной прямой и имеют одинаковую длину;
- Противоположные лучи не могут быть параллельными, так как они направлены в разные стороны.
Противоположные лучи являются важным элементом при изучении геометрии и находят применение в различных областях знаний, таких как решение задач, конструирование и анализ геометрических объектов.
Свойства противоположных лучей и их применение в геометрии 7
Одно из основных свойств противоположных лучей заключается в том, что они образуют прямую линию. Таким образом, если два противоположных луча AB и AC имеют общее начало A, то они могут быть продолжены в одном направлении, чтобы сформировать прямую линию. Это свойство позволяет использовать противоположные лучи для построения отрезков и прямых линий на плоскости.
Другое важное свойство противоположных лучей - равенство. Если два противоположных луча имеют одну и ту же длину и направление, то они считаются равными. Это свойство можно использовать для измерения длины отрезков и относительного расположения точек на плоскости.
Противоположные лучи также могут быть использованы для определения углов. Если луч AC делит угол CAB на два равных угла, то лучы AC и AB считаются противоположными. Это свойство позволяет использовать противоположные лучи для изучения геометрических углов и их свойств.
В геометрии 7 противоположные лучи часто используются при решении задач на построение геометрических фигур. Например, для построения равнобедренного треугольника можно воспользоваться свойством противоположных лучей - продолжить сторону треугольника, чтобы получить противоположные лучи, а затем провести прямую через их общее начало и середину продолженной стороны.
Таким образом, свойства противоположных лучей играют важную роль в геометрии 7. Они помогают в построении геометрических фигур и решении задач, а также позволяют изучать углы и относительное расположение точек на плоскости.



