Производная – понятие, изучаемое в математике, которое играет важную роль в анализе функций. Она позволяет определить изменение величины функции в зависимости от ее аргумента. Производная позволяет выявлять экстремумы функций, а также их поведение в окрестности определенной точки.
Чтобы найти производную функции, необходимо использовать правила дифференцирования и определенные формулы. Один из основных способов вычисления производной – использование дифференциальных операторов, таких как дифференциал. Производная является пределом отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю.
Если функция задана аналитически, то для нахождения ее производной могут применяться такие методы, как дифференцирование по правилу сложной функции, дифференцирование по правилу суммы функций, дифференцирование по правилу произведения функций и т.д.
Производные функций используются в различных областях науки и техники. Они находят применение в физике, экономике, биологии и других дисциплинах. Понимание производной и умение находить ее является важным навыком для работы с функциями и анализа различных явлений.
Определение и суть производной

Формально, производная функции f(x) в точке x определяется как предел изменения функции при бесконечном приближении аргумента:
Численно значение производной можно представить как отношение изменения функции к изменению ее аргумента в сколь угодно малом интервале. Иными словами, производная показывает наклон касательной к графику функции в данной точке.
Производная имеет множество применений в различных областях науки и инженерии, таких как физика, экономика, биология и другие. Она позволяет анализировать тенденции, предсказывать будущие значения функции, оптимизировать процессы и даже находить точки минимума и максимума функции. Без производной было бы невозможно точно моделировать и изучать различные явления и процессы.
Формулы и правила нахождения производной
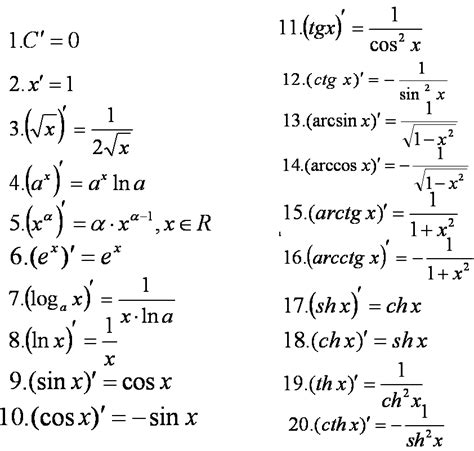
Ниже представлены основные формулы и правила нахождения производной:
1. Правило суммы: производная суммы двух функций равна сумме производных этих функций. Если f(x) и g(x) являются дифференцируемыми функциями, то (f(x) + g(x))' = f'(x) + g'(x).
2. Правило произведения числа на функцию: производная произведения числа на функцию равна произведению числа на производную функции. Если c является постоянным числом и f(x) является дифференцируемой функцией, то (c*f(x))' = c*f'(x).
3. Правило произведения функций: производная произведения двух функций равна произведению первой функции на производную второй функции, плюс произведение второй функции на производную первой функции. Если f(x) и g(x) являются дифференцируемыми функциями, то (f(x)*g(x))' = f'(x)*g(x) + f(x)*g'(x).
4. Правило частного: производная частного двух функций равна разности произведения первой функции на производную второй функции и произведения второй функции на производную первой функции, делённая на квадрат второй функции. Если f(x) и g(x) являются дифференцируемыми функциями и g(x) не равна 0, то (f(x)/g(x))' = (f'(x)*g(x) - f(x)*g'(x)) / (g(x))^2.
5. Правило цепочки: производная сложной функции равна произведению производной внешней функции на производную внутренней функции. Если u(x) и v(x) являются дифференцируемыми функциями, то (f(g(x)))' = f'(g(x)) * g'(x).
6. Правило степени: производная функции, которая является степенной функцией, равна произведению показателя степени на основание степени, умноженного на производную основания степени. Если f(x) = x^n, где n является постоянным числом, то f'(x) = n*x^(n-1).
Это лишь некоторые основные формулы и правила для нахождения производной. С их помощью возможно вычисление производной сложных функций и даже функций высокого порядка.
Понятие и значение производной в математике

Производная функции f(x) обозначается как f'(x) или dy/dx и определяется как предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю:
| Функция | Производная |
|---|---|
| f(x) | f'(x) или dy/dx |
Величина производной в каждой точке характеризует наклон касательной к графику функции в этой точке. Если значение производной положительно, то функция возрастает в данной точке, если отрицательно – убывает, а если равно нулю – функция имеет экстремум.
Производная также используется для нахождения критических точек функции, определения точек минимума и максимума, составления уравнения касательной линии и многих других применений в математике и физике.
Производная функции: основные свойства
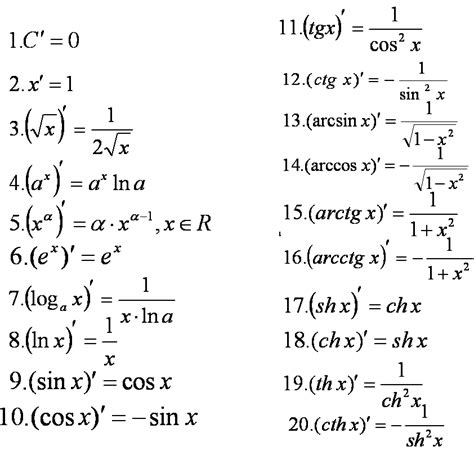
Существуют несколько основных свойств производной функции, которые используются при ее нахождении:
1. Линейность: Если функция f(x) и g(x) имеют производные в точке x, а также заданы константы a и b, то производная от (a*f(x) + b*g(x)) равна a * f'(x) + b * g'(x).
2. Правила дифференцирования: Существуют определенные правила (например, правило сложения, правило произведения, правило дифференцирования степенной функции), которые позволяют находить производную сложных функций.
3. Производная произведения: Производная произведения двух функций равна произведению производных этих функций, умноженному на первую функцию, плюс произведение первой функции на производную второй функции.
4. Производная частного: Производная частного двух функций равна разности произведения производной первой функции на вторую функцию и произведения первой функции на производную второй функции, деленной на квадрат второй функции.
Знание этих основных свойств и правил дифференцирования позволяет находить производные различных функций, а также проводить дальнейшие исследования и оптимизацию функций.
Непрерывность функций и их производных

Производная функции показывает, как быстро меняется значение функции в зависимости от изменения ее аргумента. Если функция имеет производную на интервале, то она называется дифференцируемой на этом интервале. Важно отметить, что дифференцируемость функции предполагает ее непрерывность на данном интервале.
Таким образом, непрерывность функции является необходимым условием для наличия ее производной на заданном интервале. Однако существуют функции, которые непрерывны, но не являются дифференцируемыми. В таком случае говорят о существовании разрыва в производной функции.
Знание свойств непрерывности функций и их производных позволяет анализировать поведение функций, определять их критические точки и экстремумы, а также проводить детальное исследование функций на данном интервале.
Примеры и задачи на нахождение производной

Для лучшего понимания производной, рассмотрим несколько примеров и попробуем решить задачи на ее нахождение.
Пример 1:
Найдите производную функции f(x) = 3x^2 + 2x - 1.
Решение: Для нахождения производной, нужно посчитать производную каждого слагаемого и сложить их. Производная константы равна нулю. Производная функции вида x^n, где n - целое число, равна n*x^(n-1).
Производная данной функции равна f'(x) = 6x + 2.
Пример 2:
Найдите производную функции f(x) = 4sin(x) + cos(x).
Решение: Производная суммы функций равна сумме их производных. Производная синуса равна косинусу, а производная косинуса равна минус синусу.
Производная данной функции равна f'(x) = 4cos(x) - sin(x).
Задача:
Найдите производную функции f(x) = x^3 - 2x^2 + 5x - 3 в точке x = 2.
Решение: Найдем производную функции, используя правила нахождения производной. Затем, подставим значение x = 2 в найденную производную.
Производная данной функции равна f'(x) = 3x^2 - 4x + 5. Подставляем x = 2 в производную и получаем значение производной в точке x = 2: f'(2) = 3*2^2 - 4*2 + 5 = 7.
В данных примерах и задачах мы рассмотрели некоторые базовые случаи и правила для нахождения производных. Однако, в реальных задачах могут быть более сложные функции, требующие применения других правил и методов для нахождения производной. Практика и примеры помогут вам лучше понять производную и использовать ее в решении задач.
Графическое представление производной
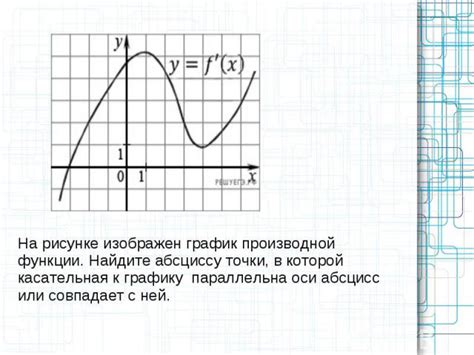
График производной функции показывает, как меняется наклон графика исходной функции. Если производная положительна в какой-то точке, то график исходной функции в этой точке возрастает (имеет положительный наклон). Если производная отрицательна, то график функции убывает (имеет отрицательный наклон).
Если производная равна нулю, то график функции имеет горизонтальную асимптоту (наклон = 0).
Таким образом, графическое представление производной функции помогает понять, как функция меняется на каждом участке своего графика и определить значения экстремумов (максимумов и минимумов).
Для построения графика производной функции можно использовать различные программы и онлайн-инструменты, а также ручное построение по значению производной в каждой точке.
Пример:
Рассмотрим функцию f(x) = x2. График этой функции имеет форму параболы с вершиной в точке (0, 0).
Если мы возьмем производную от функции f(x), то получим f'(x) = 2x. График производной функции будет представлять собой прямую пропорциональную значению x.
Таким образом, график производной функции f'(x) = 2x будет проходить через точку (0,0) и будет являться наклонной прямой, проходящей через начало координат.
Этот пример демонстрирует, как графическое представление производной позволяет наглядно увидеть изменение функции и ее наклон в каждой точке.
Производная в прикладных задачах

Одним из примеров задач, где производная играет ключевую роль, является задача оптимизации. Например, представим себе задачу о максимизации прибыли при производстве товара. Для решения этой задачи необходимо определить точку максимума функции, описывающей зависимость прибыли от производства. Для этого находим производную функции прибыли, приравниваем ее к нулю и находим соответствующую точку на графике. Эта точка будет представлять максимальную прибыль.
Другой пример применения производной – задача на определение скорости и ускорения движения. Например, при изучении движения материальной точки можно определить ее скорость в каждый момент времени, а также ускорение, исходя из изменения ее координаты. Для этого необходимо взять производные функций, описывающих изменение координаты точки от времени.
Производная также может быть использована для определения точек перегиба на графике функции. Эти точки представляют собой места, где график функции меняет свое изгибление. Например, в задаче на определение доли отказов при работе оборудования можно использовать производную функции доли отказов для определения точки перегиба, которая будет указывать на наиболее надежную долю работы оборудования.



