Рациональная дробь – это число, которое можно представить в виде отношения двух целых чисел. В математике рациональные дроби являются основным классом чисел, включающим как целые числа, так и десятичные дроби. Они играют важную роль в различных областях науки, техники и финансов.
Представление числа в виде рациональной дроби осуществляется путем записи числителя и знаменателя через символ дроби, обычно заключенный в скобки или через десятичную запятую. Например, 3/4 или 0,75. Числитель и знаменатель могут быть большими или маленькими целыми числами или десятичными дробями, в зависимости от вида представляемого числа.
Рациональные дроби используются во многих областях, включая физику, экономику, статистику и инженерию. Они позволяют точно описывать и вычислять дробные и десятичные значения, что имеет огромное значение для решения различных задач и принятия обоснованных решений.
Что такое рациональная дробь?

Рациональные дроби широко применяются в математике, физике, экономике и других науках для описания долей, коэффициентов и пропорций. Они позволяют представить дробные значения точно и компактно, что делает их удобными для использования и анализа.
Рациональные дроби могут быть положительными или отрицательными, десятичными или обыкновенными. В обыкновенной форме рациональной дроби числитель и знаменатель записываются отдельно, разделенные знаком "/". Например, дробь 3/4 представляет собой рациональное число, где числитель равен 3, а знаменатель равен 4.
Рациональная дробь может быть также записана в десятичной форме. В этом случае, десятичная запись представляет собой конечную или бесконечную последовательность цифр после запятой. Десятичная запись рациональной дроби может быть преобразована в десятичную дробь путем деления числителя на знаменатель.
| Обыкновенная форма | Десятичная форма |
|---|---|
| 1/2 | 0.5 |
| -3/4 | -0.75 |
| 2/3 | 0.6666... |
Рациональные дроби могут использоваться для решения различных математических задач, включая доли, пропорции, проценты и т. д. Они также могут быть использованы для представления результатов вычислений, таких как сложение, вычитание, умножение и деление.
Важно отметить, что рациональные дроби являются одним из базовых понятий алгебры и имеют широкий спектр применений. Понимание и умение работать с рациональными дробями является необходимым навыком для многих областей знаний и профессий.
Как представить число в виде рациональной дроби?

Для рациональных чисел с конечным десятичным представлением процесс представления в виде дроби прост. Например, для числа 0.75 мы можем записать его в виде 3/4.
Однако, для чисел с бесконечной десятичной дробью, таких как 0.3333... (1/3) или 0.142857142857... (1/7), процесс представления в виде обыкновенной дроби более сложный.
Мы можем использовать математические методы, чтобы преобразовать бесконечные десятичные дроби в рациональные дроби. Например, для числа 0.3333... мы можем обозначить его как x и затем умножить на 10, чтобы получить 10x. Следующим шагом будет вычитание x из 10x, что даст нам 9x. Затем мы можем разделить 9x на 9, чтобы получить x = 1/3.
Аналогичные методы используются для представления других бесконечных десятичных дробей в виде рациональных дробей. Эти методы могут включать нахождение периодического или непериодического закона повторения десятичных цифр и применение алгоритмов для нахождения общих множителей или составления системы уравнений.
Итак, представление числа в виде рациональной дроби требует решения математических задач, включающих деление, умножение, вычитание и извлечение корней. Такие представления позволяют нам работать с числами более удобным способом и выполнять различные математические операции.
Примеры представления чисел в виде рациональных дробей
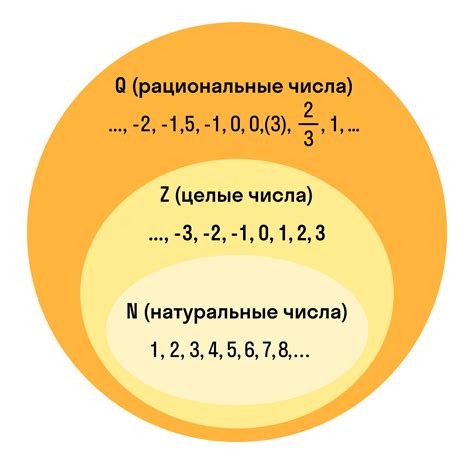
Примеры представления чисел в виде рациональных дробей:
- 1/2 - дробь, где числитель равен 1, а знаменатель равен 2. Это означает, что число 1/2 представляет половину единицы.
- 3/4 - дробь, где числитель равен 3, а знаменатель равен 4. Это означает, что число 3/4 представляет три четверти единицы.
- 5/8 - дробь, где числитель равен 5, а знаменатель равен 8. Это означает, что число 5/8 представляет пять восьмых единицы.
- 2/3 - дробь, где числитель равен 2, а знаменатель равен 3. Это означает, что число 2/3 представляет две трети единицы.
- 7/10 - дробь, где числитель равен 7, а знаменатель равен 10. Это означает, что число 7/10 представляет семь десятых единицы.
Представление чисел в виде рациональных дробей позволяет нам точно определить долю или доли числа по отношению к единице. Это важный концепт, который широко используется в математике, физике, экономике и других областях науки и техники.



