Площадь – одно из ключевых понятий математики, которое изучается уже в третьем классе. Это величина, которая позволяет определить, сколько плоскости занимает данная фигура. Знание площади позволяет решать множество задач в геометрии, а также в повседневной жизни.
Основное правило для расчета площади в 3 классе – это умение составить прямоугольник или квадрат с такими же размерами, какие имеет изучаемая фигура. Для этого нужно "залить" контур фигуры внутри прямоугольника и посчитать количество квадратных клеток, занимаемых этой фигурой.
Знание площади позволяет решать различные задачи, такие как вычисление площади комнаты в доме или расчет количества плиток для покрытия пола. Понимание этого важного понятия позволяет детям развивать свои математические навыки и логическое мышлениес самого раннего возраста.
Площадь: определение и примеры из школьной программы 3 класса математики
Примеры вычисления площади в 3 классе включают в себя простые геометрические фигуры, с которыми дети знакомятся в рамках школьной программы:
| Фигура | Формула для вычисления площади | Пример |
|---|---|---|
| Прямоугольник | Площадь = длина * ширина | Для прямоугольника со сторонами 4 и 6: Площадь = 4 * 6 = 24 единицы площади |
| Треугольник | Площадь = (основание * высота) / 2 | Для треугольника с основанием 5 и высотой 8: Площадь = (5 * 8) / 2 = 20 единиц площади |
| Круг | Площадь = π * радиус^2 | Для круга с радиусом 3: Площадь = 3.14 * 3^2 = 28.26 единиц площади |
Знание площади позволяет детям измерять и сравнивать размеры различных фигур, а также использовать эту информацию для решения задач и построения дополнительных геометрических фигур.
Что такое площадь и как она вычисляется?

Вычисление площади различных фигур может быть сложной задачей, но существуют некоторые правила и формулы, которые могут помочь нам в этом процессе.
Ниже перечислены некоторые универсальные формулы для вычисления площадей:
- Площадь прямоугольника: S = a * b, где а и b – длины сторон прямоугольника.
- Площадь квадрата: S = a * a, где a – длина стороны квадрата.
- Площадь треугольника: S = 0.5 * a * h, где a – длина основания треугольника, h – высота от основания к вершине.
- Площадь круга: S = π * r * r, где π – математическая константа, равная примерно 3.14159, r – радиус круга.
Определение площади фигуры может быть полезным при решении различных задач, таких как расчет площади помещения, вычисление площади поля или сада и т.д.
Простые правила для вычисления площади фигур в 3 классе
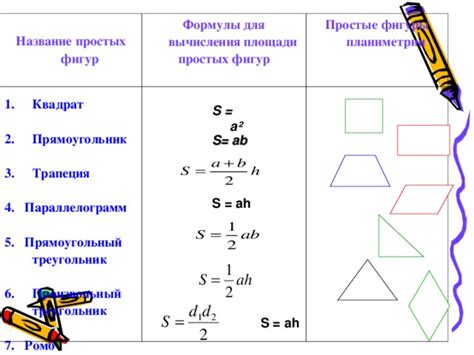
- Площадь прямоугольника: чтобы найти площадь прямоугольника, нужно умножить длину на ширину.
- Площадь квадрата: площадь квадрата можно найти, умножив длину одной стороны на себя. Ведь все стороны у квадрата равны!
- Площадь треугольника: формула для вычисления площади треугольника - умножить длину основания на высоту и делить на 2.
- Площадь круга: чтобы найти площадь круга, нужно умножить квадрат радиуса на число Пи (π), приближенно равное 3,14.
Запомни эти простые правила, чтобы с легкостью вычислять площадь разных фигур. Это поможет тебе не только в математике, но и в повседневной жизни, например, при покупке ковра или рассчете площади комнаты.
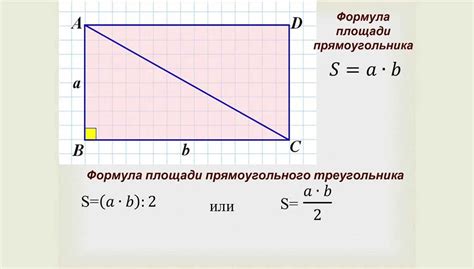
Как вычислить площадь прямоугольника?
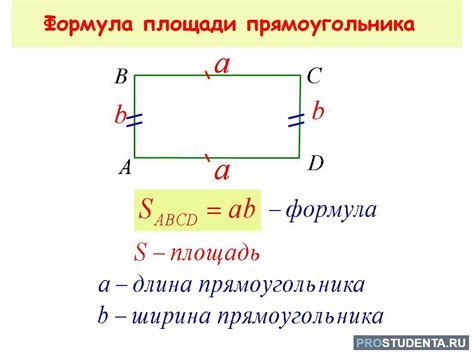
Формула для вычисления площади прямоугольника очень простая:
| Площадь прямоугольника (S) | = Длина (a) * Ширина (b) |
Для того чтобы найти площадь прямоугольника, необходимо знать значение его длины и ширины. Длина прямоугольника - это сторона, которая больше, а ширина - это сторона, которая меньше.
Допустим, у нас есть прямоугольник со сторонами 5 см и 3 см. Чтобы вычислить площадь этого прямоугольника, нужно умножить длину на ширину:
| Площадь прямоугольника (S) | = 5 см * 3 см | = 15 см² |
Таким образом, площадь прямоугольника равна 15 квадратным сантиметрам.
Примеры вычисления площади прямоугольника

Для вычисления площади прямоугольника необходимо знать его длину и ширину. Площадь представляет собой произведение этих двух величин.
Пример 1:
Пусть длина прямоугольника равна 5 см, а ширина равна 3 см. Для вычисления площади прямоугольника умножаем эти два числа: 5 см * 3 см = 15 см².
Пример 2:
Если известны стороны прямоугольника в метрах, то площадь будет выражаться в квадратных метрах. Пусть длина прямоугольника равна 2 м, а ширина равна 4 м. Умножаем длину на ширину: 2 м * 4 м = 8 м².
Пример 3:
Если прямоугольник с заданными сторонами уже изображен на графическом листе, площадь можно вычислить посредством замеров на местности. Например, длина прямоугольника равна 10 см, а ширина равна 6 см. Площадь будет равна 10 см * 6 см = 60 см².
Как найти площадь треугольника?
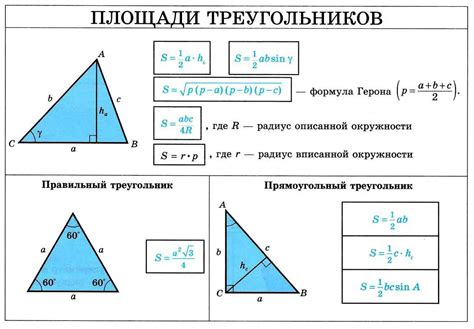
Площадь треугольника можно найти с помощью простых математических формул. Существует несколько способов вычисления площади треугольника, в зависимости от данных, которыми вы располагаете.
1. Если у вас есть длина основания треугольника и высота, проведенная к этому основанию:
- Умножьте длину основания на высоту треугольника (длина * высота)
- Разделите полученное значение на 2
2. Если у вас есть длины всех трех сторон треугольника:
- Используйте формулу Герона: S = sqrt(p * (p - a) * (p - b) * (p - c)), где "p" - полупериметр треугольника, "a", "b", "c" - длины сторон
3. Если у вас есть координаты вершин треугольника на плоскости:
- Используйте формулу площади треугольника по координатам: S = 0.5 * |(x1 * (y2 - y3) + x2 * (y3 - y1) + x3 * (y1 - y2))|, где "x1", "x2", "x3" - координаты вершин по оси X, "y1", "y2", "y3" - координаты вершин по оси Y
Будьте внимательны при подсчете площади треугольника, чтобы правильно использовать формулы и получить точный результат.
Примеры вычисления площади треугольника:

Для вычисления площади треугольника нужно знать его высоту и основание.
Пример 1:
Пусть треугольник имеет высоту 4 см и основание 8 см.
Площадь треугольника равна половине произведения высоты на основание:
S = (4 см * 8 см) / 2 = 16 см²
Ответ: площадь треугольника равна 16 см².
Пример 2:
Допустим, вы знаете, что треугольник имеет высоту 5 м и основание 10 м.
Аналогично, площадь треугольника будет равна:
S = (5 м * 10 м) / 2 = 25 м²
Ответ: площадь треугольника равна 25 м².
Как определить площадь квадрата?

Площадь квадрата можно определить, зная длину его стороны. В случае квадрата все стороны равны между собой, поэтому для определения площади достаточно знать длину одной из сторон.
Формула для нахождения площади квадрата проста: площадь равна квадрату длины стороны.
Математически записать формулу можно так: S = a^2, где S - площадь квадрата, a - длина стороны.
Например, если длина стороны квадрата равна 5 см, то площадь будет равна 5^2 = 25 см^2. Если длина стороны квадрата измеряется в метрах, то площадь будет измеряться в квадратных метрах.
Определение площади квадрата может пригодиться при решении задач по геометрии и измерениям. Зная площадь квадрата, можно определить его площадь дальше можно использовать для нахождения площади других фигур, например, прямоугольника, разбивая его на квадраты и суммируя их площади.
| Пример: | Решение: |
|---|---|
| Сторона квадрата: 8 см | Площадь квадрата: 8^2 = 64 см^2 |
| Сторона квадрата: 3 м | Площадь квадрата: 3^2 = 9 м^2 |
Примеры вычисления площади квадрата
Рассмотрим примеры вычисления площади квадрата для разных значений стороны.
| Сторона квадрата (а) | Площадь квадрата (S) |
|---|---|
| 2 см | 4 см² |
| 5 м | 25 м² |
| 10 см | 100 см² |
| 3 м | 9 м² |
Таким образом, площадь квадрата прямо пропорциональна квадрату длины его стороны.
Зачем нужно знать площадь и как это помогает в повседневной жизни?
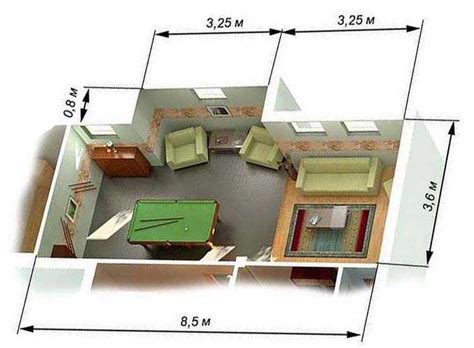
Например, знание площади позволяет нам определить, сколько квадратных метров занимает определенная площадь нашего основного жилья. Это может быть полезно при покупке ковра или расчете количества стекла, необходимого для облицовки окон. Также знание площади помогает нам решать задачи по обустройству сада или участка, определять, сколько растений будет помещаться на определенной площади или сколько краски потребуется для покраски стен.
Знание площади также полезно при обустройстве кухни или гостиной. Оно позволяет правильно подобрать мебель и определить, сколько квадратных метров занимают определенные предметы, такие как столы, стулья или шкафы. Благодаря этому мы можем планировать пространство так, чтобы все предметы помещались без проблем.
Кроме того, знание площади помогает нам разобраться в географии и архитектуре. Мы можем измерять площадь стран, городов, зданий и других объектов, чтобы лучше понимать их размеры. Это помогает нам сформировать представление о разных местах и способах их использования.
В общем, знание площади играет важную роль в нашей повседневной жизни, помогая нам решать различные задачи, планировать пространство и лучше понимать окружающий нас мир.



