Пирамида - это геометрическое тело, которое обладает особыми свойствами и имеет характерную форму стороны, напоминающую треугольник. Однако пирамида отличается от обычного треугольника тем, что у нее есть вершина и боковые грани, которые сходятся в этой вершине. Именно поэтому пирамида считается одним из основных элементов геометрии и используется в различных науках и отраслях человеческой деятельности.
Апофема пирамиды - это величина, которая является высотой боковой грани пирамиды и противоположна ей по отношению к основанию. Это расстояние олицетворяет глубину и мощность пирамиды и важно при изучении и анализе ее свойств и характеристик. Апофема пирамиды должна быть измерена от вершины пирамиды до середины самой длинной боковой грани и может быть представлена как формула или числовое значение.
Примером пирамиды с измеренной апофемой может служить Эгипетская пирамида Хеопса - одно из Семи чудес света. Эта пирамида имеет основание в форме квадрата и четыре боковые грани, сходящиеся в вершине. Апофема этой пирамиды составляет около 186.4 метра и является одной из ключевых характеристик этого удивительного сооружения.
Что такое пирамида и как она определяется
Одной из наиболее известных примеров пирамиды является Египетская пирамида. Египетские пирамиды, сооруженные в Древнем Египте, являются одним из семи чудес древнего мира. Они имеют квадратную или прямоугольную форму основы и аккуратные треугольные грани, сходящиеся в вершину.
Пирамида является одним из важных геометрических тел, так как она присутствует в различных сферах нашей жизни. Например, горные вершины часто имеют форму пирамиды. Кроме того, пирамиды используются в архитектуре для построения зданий и монументов, а также в математике и физике для изучения геометрии и пространственных отношений.
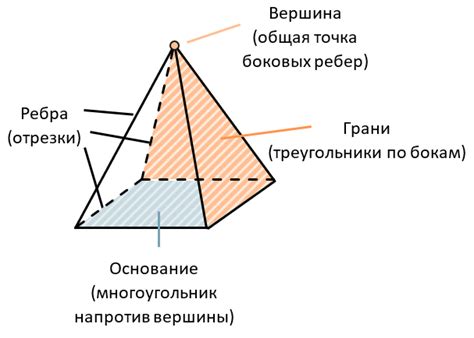
Основные понятия и сущность пирамиды

Одной из важных характеристик пирамиды является ее высота. Высота пирамиды - это расстояние от вершины до плоскости основания, принято обозначать буквой h. В зависимости от формы основания пирамида может быть правильной или неправильной. В правильной пирамиде все грани имеют одинаковую форму и равные углы между собой.
Площадь основания пирамиды - это площадь замкнутой плоской фигуры, на которую опирается пирамида. Обозначается буквой S. Площадь основания является важным параметром при расчетах объема и других характеристик пирамиды.
Объем пирамиды - это мера пространства, занимаемого пирамидой. Вычисляется по формуле V = (1/3) * S * h, где S - площадь основания пирамиды, а h - высота пирамиды. Объем пирамиды измеряется в кубических единицах.
Пирамиды широко используются в архитектуре, искусстве, математике и других областях. Они являются символами силы, могущества и мистических знаний. Примерами известных пирамид являются пирамида Хеопса в Гизе, Луврская пирамида во Франции и пирамида Майя в Чичен-Ице.
| Вид пирамиды | Пример | Форма основания |
|---|---|---|
| Тетраэдр | Пирамида Хеопса | Треугольник |
| Гексаэдр | Луврская пирамида | Квадрат |
| Октаэдр | Пирамида Майя | Восьмиугольник |
Примеры апофемы пирамиды в архитектуре и математике

Вот несколько примеров пирамид в архитектуре:
- Пирамиды Гизы, Египет: Самые известные пирамиды на планете, включая Гизскую пирамиду Хеопса, Хефрена и Микерина.
- Пирамиды Месоамерики: Как часть различных майянских и ацтекских городов, пирамиды месоамерики имеют особую архитектуру и высоту.
- Пирамида Солнца, Мексика: Расположенная в археологическом комплексе Теотиуакан, пирамида Солнца является самым высоким сооружением в Теотиуакане и одной из крупнейших пирамид в мире.
- Пирамиды Южной Америки: Некоторые из наиболее известных пирамид в Южной Америке находятся в Чавин-де-Хуантар и Сипане.
Помимо архитектуры, пирамиды также используются в математике для описания и исследования различных фигур и моделей. Апофема пирамиды - это расстояние от апекса пирамиды до центра основания. Вот некоторые примеры использования апофемы пирамиды в математике:
- Вычисление объема пирамиды на основе апофемы и высоты.
- Расчет площади боковой поверхности пирамиды, используя апофему и периметр основания.
- Изучение свойств и формул для разных типов пирамид, таких как правильные пирамиды и усеченные пирамиды.
- Использование апофемы для решения различных геометрических задач, связанных с пирамидами.
В архитектуре и математике, апофема пирамиды играет важную роль в определении размеров и свойств этой уникальной формы. Она помогает разработчикам и исследователям лучше понимать и использовать пирамиды для своих нужд.



