Отношение в геометрии – это одно из базовых понятий, которое помогает нам понять, как связаны между собой различные геометрические фигуры и объекты. Оно дает возможность описать взаимосвязь различных сторон, углов или длин, позволяя нам разбираться в сложных пространственных конструкциях.
Отношение может быть выражено числом или формулой, которая показывает соотношение между разными сторонами или углами в геометрическом объекте. Например, можно рассмотреть отношение между длиной основания и площадью прямоугольника, а также отношение между диагоналями и сторонами квадрата.
Важно понимать, что отношение в геометрии может быть как прямым, так и обратным. Прямое отношение означает, что при увеличении или уменьшении одной стороны или угла, другая сторона или угол будут изменяться пропорционально. Обратное отношение, наоборот, означает, что увеличение одной стороны или угла может привести к уменьшению другой или наоборот.
Отношение в геометрии играет важную роль в понимании форм, размеров и свойств различных фигур. Благодаря ему мы можем проводить различные математические операции с геометрическими объектами, а также решать разнообразные задачи на нахождение неизвестных величин. Отношение в геометрии является основой для понимания пропорций, подобия и других важных концепций.
Определение понятия отношения в геометрии
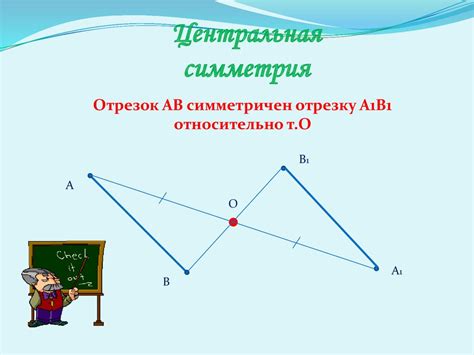
Отношение может быть определено на основе различных свойств объектов. Например, в геометрии отношение симметричности используется для описания объектов, которые могут быть симметричными относительно определенной точки, оси или плоскости. Отношение включения описывает ситуацию, когда один объект целиком содержится внутри другого объекта.
Отношение в геометрии может быть также использовано для определения различных типов треугольников, таких как равносторонний, равнобедренный или прямоугольный. В этом случае отношение основано на соотношении длин сторон и углов треугольника. Отношение также может быть использовано для определения площади и объема различных геометрических фигур.
Свойства отношений в геометрии
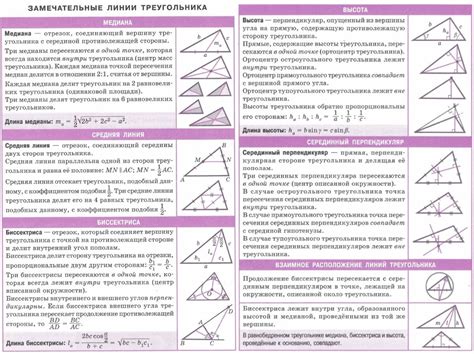
1. Соотношение длин: Один из основных типов отношений в геометрии – отношение длин. Ученики учатся сравнивать длины отрезков и устанавливать, когда они равны, меньше или больше друг друга. Для сравнения длин используются математические операции сравнения, такие как «больше», «меньше» или «равно».
2. Соотношение площадей: Другим важным свойством отношений в геометрии является отношение площадей. Ученики учатся сравнивать площади различных фигур и выражать их отношения в виде дробей или процентов. Они также изучают, как изменяется площадь при изменении размеров фигуры.
3. Соотношение углов: Ещё одно важное свойство отношений в геометрии – отношение углов. Ученики учатся сравнивать углы и анализировать их величину. Они изучают, как связаны углы в треугольниках и четырехугольниках, и решают задачи на определение неизвестных углов.
4. Соотношение объемов и площадей поверхностей: В более продвинутых заданиях ученики изучают отношения объемов и площадей поверхностей различных трехмерных фигур. Они сравнивают объемы и площади, решают задачи на нахождение неизвестных данных, и анализируют изменение объемов и площадей при изменении размеров фигур.
Как представить отношение в геометрии
Отношение в геометрии представляет собой соотношение между двумя или более объектами. В геометрии отношения могут быть выражены при помощи различных понятий, таких как подобие, равенство, параллельность и перпендикулярность.
Подобие - это отношение между двумя фигурами, когда все соответствующие стороны и углы у них пропорциональны. Например, если два треугольника имеют одинаковые углы, и их стороны пропорциональны, то они являются подобными.
Равенство - это отношение, которое означает, что две фигуры имеют одинаковую длину или площадь. Например, если две отрезка имеют одинаковую длину, то они равны.
Параллельность - это отношение между двумя прямыми линиями, которые не пересекаются ни в одной точке. Например, если две прямые линии находятся на одной плоскости и не пересекаются, то они параллельны.
Перпендикулярность - это отношение между двумя линиями, когда они пересекаются, образуя прямые углы. Например, если две линии пересекаются и образуют прямой угол, то они перпендикулярны.
Представление отношений в геометрии помогает установить связь между различными фигурами и использовать их свойства для решения геометрических задач. Знание отношений в геометрии позволяет анализировать и предсказывать свойства и взаимосвязь геометрических объектов.
Отношение между прямыми и плоскостями
Если прямая лежит в плоскости, то говорят, что она пересекает эту плоскость. В случае, если прямая лежит в плоскости и не пересекает ее, то говорят, что она параллельна плоскости.
Отношение между прямыми и плоскостями можно также определить с помощью угловой меры. Если прямая и плоскость пересекаются и образуют между собой угол, то этот угол называется прямым углом. В случае, если прямая и плоскость пересекаются и образуют между собой угол, который меньше или больше прямого угла, то говорят, что угол тупой или острый.
Отношение между прямыми и плоскостями может быть также определено с помощью расстояния между ними. Если расстояние между прямой и плоскостью равно нулю, то прямая лежит в плоскости. В случае, если расстояние между прямой и плоскостью больше нуля, то прямая пересекает плоскость.
Отношение между прямыми и плоскостями имеет важное значение при решении геометрических задач. Например, знание того, что прямая параллельна плоскости, позволяет найти точку пересечения прямой и плоскости. Аналогично, знание того, что прямая пересекает плоскость, позволяет найти точку пересечения прямой и плоскости и определить угол между ними.
В итоге, понимание отношения между прямыми и плоскостями является фундаментальным для понимания геометрии и позволяет анализировать пространственные конфигурации с помощью геометрических методов.
Отношение между углами

В геометрии отношение между углами определяется их взаимным расположением и величинами. Рассмотрим основные типы отношений между углами.
1. Вертикальные углы - это пары углов, расположенных друг напротив друга при пересечении двух прямых. Вертикальные углы всегда равны друг другу. Это свойство позволяет применять их для решения геометрических задач.
2. Смежные углы - это пары углов, имеющих общую сторону и общую вершину. Сумма смежных углов всегда равна 180 градусов. Это свойство полезно при решении задач на нахождение неизвестных углов.
3. Взаимно внутренние углы - это пары углов, расположенных внутри двух параллельных прямых и пересеченных третьей прямой. Взаимно внутренние углы равны между собой. Они используются при решении задач на нахождение неизвестных углов и нахождение параллельных прямых.
4. Взаимно внешние углы - это пары углов, расположенных внешне двух параллельных прямых и пересекаемых третьей прямой. Взаимно внешние углы равны между собой. Они применяются при решении задач на нахождение неизвестных углов и нахождение параллельных прямых.
Использование знания об отношении между углами помогает решать разнообразные геометрические задачи, а также облегчает понимание и построение различных геометрических фигур.
Отношение между отрезками
В геометрии отношение между отрезками определяется как соотношение их длин. Отношение может быть равным, больше или меньше. Чтобы установить отношение между двумя отрезками, необходимо найти их длины и сравнить их между собой.
Отношение равенства обозначается символом "=", что означает, что длины двух отрезков равны. Например, если отрезок AB равен отрезку CD, то можно записать AB = CD. Это означает, что длины этих отрезков равны.
Отношение больше обозначается символом ">", что означает, что один отрезок больше другого по длине. Например, если отрезок AB больше отрезка CD, то можно записать AB > CD. Это означает, что длина отрезка AB больше длины отрезка CD.
Отношение меньше обозначается символом "
Отношение между отрезками играет важную роль в геометрии, позволяя сравнивать и классифицировать отрезки по их длине. Отношение между отрезками также является основой для других геометрических понятий, таких как подобие и пропорции.
Аналитический подход к отношениям в геометрии

В геометрии отношение между точками, отрезками или другими геометрическими фигурами можно изучать с помощью аналитического подхода. Аналитическая геометрия основана на использовании координатных систем и алгебраических методов для изучения геометрических объектов.
В аналитической геометрии точки на плоскости и в пространстве обычно представляются парой чисел, называемых координатами. Координаты точки на плоскости обозначаются обычно как (x, y), а координаты точки в пространстве - как (x, y, z), где x, y и z - числа. Таким образом, мы можем определить отношение между двумя точками, вычислив разницу их координат.
Отношение между отрезками можно также анализировать с помощью аналитического подхода. Для этого необходимо вычислить длины отрезков и сравнить их значения. Если длина одного отрезка в два раза больше длины другого отрезка, то мы можем сказать, что отношение между этими отрезками равно 1:2.
Одним из важных применений аналитического подхода в геометрии является вычисление расстояний между точками или отрезками. Для этого используются формулы, основанные на теореме Пифагора и других математических принципах. Например, расстояние между двумя точками на плоскости можно вычислить по формуле: √((x2 - x1)^2 + (y2 - y1)^2), где (x1, y1) и (x2, y2) - координаты точек.
Таким образом, аналитический подход позволяет изучать отношения между геометрическими объектами с помощью координат и математических операций. Этот подход широко используется в геометрии, физике, инженерии и других науках.
Задачи на отношения в геометрии
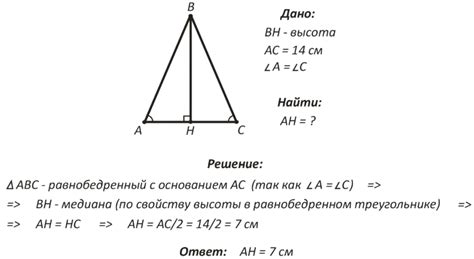
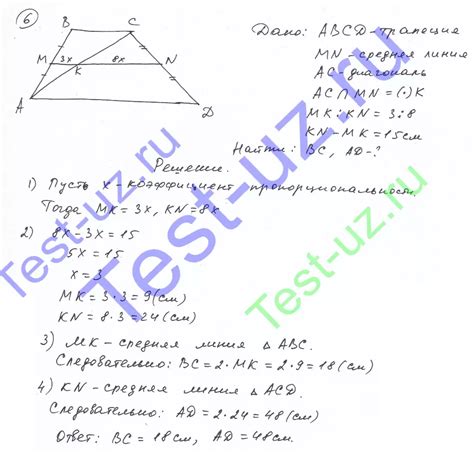
Отношения в геометрии играют важную роль при решении различных задач. Вот несколько примеров задач, в которых необходимо использовать понятие отношения:
- Найти соотношение длин двух отрезков. Для этого нужно определить, какая из длин больше или меньше, и возможно ли выразить одну длину через другую с помощью отношения.
- Найти соотношение площадей двух фигур. Для этого нужно выразить площадь одной фигуры через площадь другой с помощью отношения.
- Решить задачу на подобие. Подобные фигуры имеют одинаковые отношения между длинами сторон. Нужно найти пропорциональные отношения между сторонами фигур и использовать их для нахождения неизвестных величин.
- Найти пропорциональное отношение между объемами двух тел. Для этого нужно знать формулы для расчета объема тел и использовать их для выражения одного объема через другой.
- Решить задачу на треугольники. Например, в задаче может быть дано, что два треугольника подобны, а одна из сторон одного треугольника в два раза больше соответствующей стороны другого треугольника. Нужно найти отношение площадей этих треугольников.
Это лишь некоторые примеры задач, в которых необходимо использовать понятие отношения в геометрии. При решении таких задач важно четко представлять себе значение отношения и правильно применять его для нахождения ответа.
Примеры применения отношений в геометрии

Отношения в геометрии играют важную роль при решении различных задач и построении геометрических фигур. Вот несколько примеров применения отношений в геометрии:
1. Отношение между сторонами треугольника: В геометрии существует три основных отношения между сторонами треугольника: равенство сторон, соотношение сторон и отношение сторон. Отношение между сторонами треугольника позволяет определить, является ли треугольник равнобедренным, равносторонним или разносторонним.
2. Отношение между диагоналями прямоугольника: В прямоугольнике диагонали имеют специальное отношение, они равны и делят прямоугольник на два равных треугольника. Это позволяет найти длину диагонали, зная длины сторон прямоугольника.
3. Отношение между радиусами и диаметрами окружности: В окружности радиусы и диаметры также имеют специальное отношение: радиус в два раза меньше диаметра. Это отношение позволяет находить радиус или диаметр окружности, если известен другой параметр.
4. Отношение между площадями подобных фигур: Подобные фигуры имеют равные отношения между сторонами и площадями. Например, если площадь одной фигуры в два раза меньше площади другой, то отношение их площадей составляет 1:2. Это справедливо для всех подобных фигур.
| Примеры отношений | Применение в геометрии |
|---|---|
| Соотношение сторон треугольника | Определение типа треугольника |
| Диагонали прямоугольника | Расчет длины диагонали и площади |
| Радиусы и диаметры окружности | Нахождение радиуса или диаметра |
| Площади подобных фигур | Определение соотношения площадей |
Таким образом, отношения в геометрии помогают анализировать и решать различные геометрические задачи, делая изучение геометрии более интересным и практичным.



