Область определения выражения в алгебре – это множество значений, которые переменные могут принимать в данном выражении. В других словах, это набор всех допустимых входных значений, которые можно использовать в математическом выражении.
Для того чтобы определить область определения выражения, необходимо учесть различные ограничения, которые могут быть наложены на переменные. Некоторые выражения могут иметь ограничения на деление на ноль, корень из отрицательного числа или использование некорректных символов.
Область определения может быть выражена в форме числового интервала или набора отдельных значений. Например, выражение x/y будет иметь область определения, в которую входят все действительные числа, за исключением нуля, так как деление на ноль невозможно.
Область определения выражения
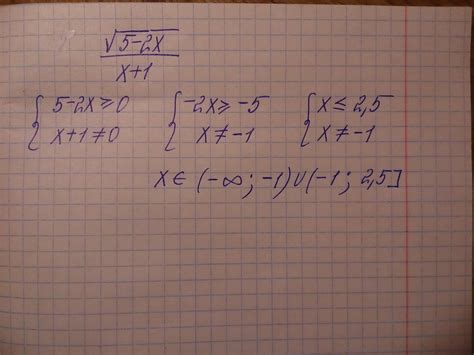
В алгебре область определения выражения представляет собой множество значений, для которых выражение имеет смысл и может быть вычислено.
Область определения зависит от типа выражения и ограничений, накладываемых на переменные в выражении. Например, в арифметических выражениях, в которых есть деление на ноль или вычисление корня из отрицательного числа, область определения будет ограничена исключением таких значений.
Определение области определения выражения является важным шагом в алгебре, поскольку позволяет определить, какие значения переменных могут быть использованы при вычислении выражения и какие значения недопустимы.
Область определения выражения может быть представлена с помощью различных математических обозначений, таких как неравенства, интервалы или условия, задающие диапазон допустимых значений переменных.
Определение и смысл

Изучение области определения важно для понимания основных свойств, ограничений и границ математических объектов. Оно позволяет определить, какие значения переменных являются допустимыми и на каких значениях выражение может быть корректно посчитано.
Область определения может быть ограничена правилами математических операций или физическими ограничениями. Например, в выражении с делением на ноль, область определения будет исключать значение переменной, при котором делитель равен нулю.
Исследование области определения выражений является неотъемлемой частью работы с алгеброй и служит основой для более глубокого понимания математических концепций и их применений.
| Пример | Область определения |
|---|---|
| Выражение: √x | x ≥ 0 |
| Выражение: 1/x | x ≠ 0 |
| Выражение: log(x) | x > 0 |
Методы определения
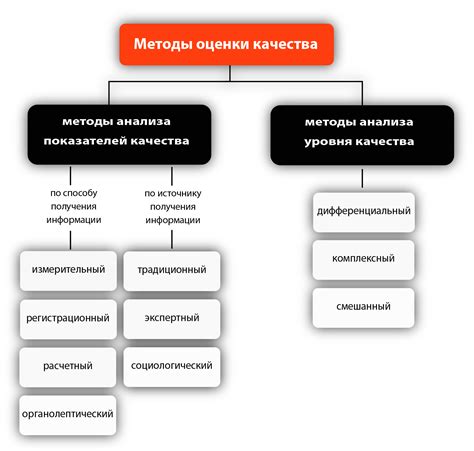
Существует несколько методов определения области определения выражения в алгебре. Представим выражение в виде функции, где множеством определения будет такое подмножество действительных чисел, при которых функция имеет смысл и не выходит за пределы допустимых значений.
Рассмотрим некоторые из наиболее распространенных методов определения области определения:
| Метод | Описание |
|---|---|
| Анализ выражения | Определяется множество значений переменных, которые могут быть подставлены в выражение, так чтобы выражение было определено. Рассматриваются основные арифметические операции и условия, которые могут привести к неопределенности. |
| Графический метод | При использовании графического метода область определения определяется по графику функции. Анализируются точки, в которых функция имеет особенности, такие как вертикальные асимптоты или точки разрыва. |
| Метод анализа пределов | Для определения области определения выражения можно использовать метод анализа пределов. Рассматриваются пределы приближения выражения к различным значениям переменных и определяются значения, при которых пределы существуют и конечны. |
| Метод проверки равенств и неравенств | Путем проверки равенств и неравенств, связанных с выражением, можно определить область определения. Если выражение нарушает какое-либо равенство или неравенство, то оно не определено в данном интервале. |
Выбор метода определения области определения зависит от сложности выражения и доступных инструментов для его анализа. Некоторые выражения могут быть более удобно определены одним методом, в то время как другие выражения требуют комбинации нескольких методов для полного определения области определения.
Примеры и применение
Область определения выражения в алгебре играет важную роль в решении уравнений и применении алгебраических методов. Рассмотрим несколько примеров, чтобы прояснить понятие области определения.
- Пример 1: Рассмотрим выражение
f(x) = \frac{1}{x}. Область определения этого выражения состоит из всех действительных чисел, кроме 0. Это связано с тем, что деление на ноль не определено в алгебре. - Пример 2: Рассмотрим выражение
g(x) = \sqrt{x}. Область определения этого выражения состоит из всех неотрицательных действительных чисел, так как корень из отрицательных чисел не определен. - Пример 3: Рассмотрим выражение
h(x) = \log{x}. Область определения этого выражения состоит из всех положительных действительных чисел, так как логарифм из отрицательных чисел и нуля не определен.
Знание области определения выражения позволяет избегать ошибок при решении уравнений и проведении алгебраических операций. Это также помогает установить границы для значений переменных в заданных выражениях, что имеет практическое применение в различных областях, таких как финансы, наука и техника.



