Математика – это один из основных предметов в школе. Она помогает детям развить логику, абстрактное мышление, а также улучшает навыки решения проблем. В 3 классе ученикам предлагается более сложный курс, включающий в себя различные темы, одной из которых является объединение.
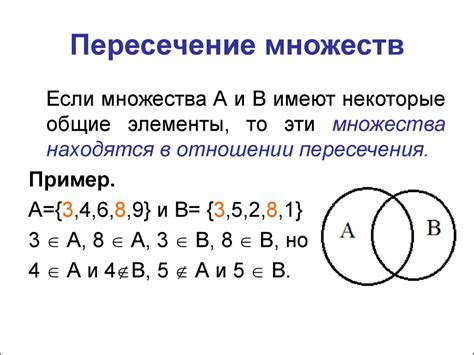
Объединение в математике – это понятие, которое позволяет объединить два или более множества в одно общее множество. Например, если у нас есть множество всех красных предметов и множество всех синих предметов, то объединение этих множеств будет включать в себя все красные и синие предметы.
Обычно объединение обозначается символом U, который означает "объединение множеств". Например, если у нас есть множество A = {1, 2, 3} и множество B = {3, 4, 5}, то их объединением будет множество C = {1, 2, 3, 4, 5}.
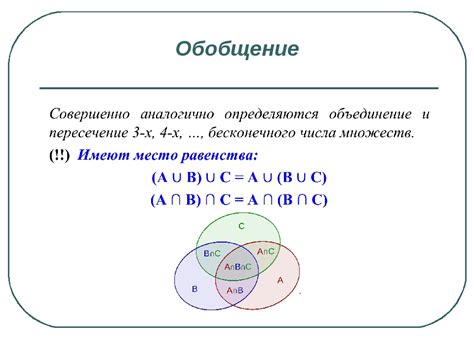
Объединение в математике важно для понимания сложных концепций, таких как объединение интервалов, объединение дробей и других. Это помогает ученикам развить аналитическое мышление и способность решать сложные задачи.
Объединение в математике 3 класс
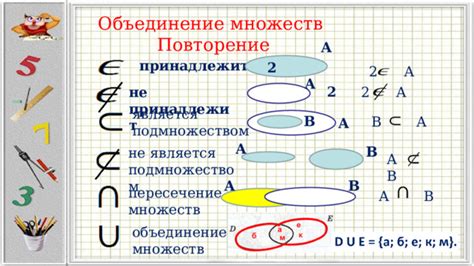
Объединение двух множеств – это операция, при которой все элементы из этих двух множеств объединяются в одно множество. Результатом объединения будет множество, содержащее все элементы из обоих исходных множеств без повторений.
Например, если имеются два множества: множество A = {1, 2, 3} и множество B = {3, 4, 5}, то их объединение будет выглядеть так: A ∪ B = {1, 2, 3, 4, 5}.
Дети в третьем классе изучают объединение с помощью примеров и задач. Они учатся находить объединение двух множеств, используя диаграммы Венна или метод перечисления элементов. Также, дети практикуются в решении задач, где необходимо найти объединение множеств по условию задачи.
Объединение в математике имеет много практических применений, например, в теории вероятности, геометрии и алгебре. Понимание объединения помогает детям развивать логическое мышление, абстрактное мышление и умение анализировать информацию.
Определение понятия "объединение"

Другими словами, при объединении мы создаем новое множество, которое содержит все элементы исходных множеств без повторений. Например, если у нас есть множество А = {1, 2, 3} и множество В = {2, 3, 4}, то объединение этих множеств будет выглядеть так: А ∪ В = {1, 2, 3, 4}.
Обозначается объединение символом ∪ (заглавная буква "ю").
Операция объединения выполняется на основе общих элементов множеств исходных множеств, исключая повторяющиеся элементы. Если элемент присутствует в одном или нескольких исходных множествах, он будет представлен только один раз в объединенном множестве.
Объединение является одной из основных операций над множествами и широко используется в математике, логике и других областях.
Как выполнять объединение множеств в математике
Объединение множеств в математике выполняется путем соединения всех элементов из двух или более множеств в одно общее множество. Результатом объединения будет множество, содержащее все уникальные элементы из каждого исходного множества.
Чтобы выполнить объединение множеств, можно использовать таблицу, где каждое множество представлено в виде строки. В столбце объединения будут располагаться элементы из всех множеств. Дубликаты удаляются, оставляя только уникальные элементы. Возможно использование дополнительных столбцов для отображения принадлежности элемента к каждому из исходных множеств.
| Множество А | Множество Б | Объединение |
|---|---|---|
| 1 | 3 | 1 |
| 2 | 4 | 2 |
| 3 | 5 | 3 |
| 6 | 4 |
В данном примере множество А содержит элементы 1, 2 и 3, множество Б содержит элементы 3, 4, 5 и 6. Результатом объединения будет множество, содержащее все уникальные элементы из обоих исходных множеств: 1, 2, 3, 4, 5 и 6.
Объединение множеств играет важную роль в математике и других областях, таких как логика, теория множеств, графика и др. Оно позволяет объединять и анализировать данные из разных источников, выявлять общие и уникальные элементы, находить пересечения и различия между множествами.
Символы, обозначающие объединение множеств
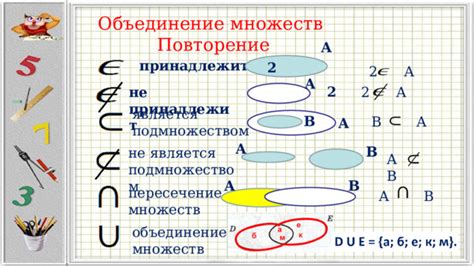
Еще одним символом, используемым для обозначения объединения множеств, является символ "∪". Этот символ также обозначает объединение двух или более множеств. Например, объединение множеств X и Y обозначается следующим образом: X ∪ Y.
Также можно использовать слова или фразы для обозначения объединения множеств. Например, можно написать "Множество A объединено с множеством B" или "Множество C и множество D объединены".
Важно понимать, что при объединении множеств элементы каждого множества сохраняются, и в итоговом множестве не будет дубликатов элементов.
| Символ | Пример использования |
|---|---|
| ∪ | A ∪ B |
| ∪ | X ∪ Y |
Примеры задач на объединение множеств для 3 класса

Рассмотрим несколько примеров задач на объединение множеств для учеников 3 класса:
| Задача | Множество A | Множество B | Результат (объединение) |
|---|---|---|---|
| Задача 1 | {1, 2, 3} | {4, 5, 6} | {1, 2, 3, 4, 5, 6} |
| Задача 2 | {a, b, c} | {c, d, e} | {a, b, c, d, e} |
| Задача 3 | {red, blue, green} | {green, yellow, orange} | {red, blue, green, yellow, orange} |
Во всех примерах результатом объединения множеств A и B является новое множество, содержащее все элементы из обоих исходных множеств без повторений. Изучение операций над множествами помогает ученикам развивать навыки анализа и логического мышления, а также позволяет применять полученные знания в повседневной жизни.
Объединение подмножеств
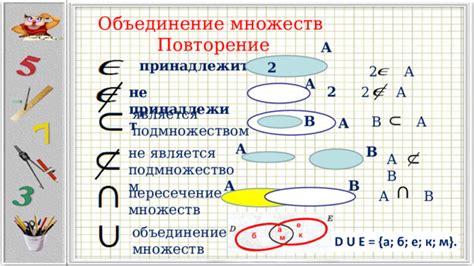
Для объединения множеств используется символ "∪" - знак объединения. Например, если у нас есть множество A = {1, 2, 3} и множество B = {3, 4, 5}, то их объединение A ∪ B будет равно {1, 2, 3, 4, 5}.
Объединение подмножеств осуществляется путем объединения элементов каждого множества без повторений. Если элемент уже присутствует в итоговом множестве, то он не добавляется повторно.
Объединение подмножеств является одной из основных операций в теории множеств и может применяться для решения различных задач. Например, при объединении двух множеств можно определить, какие элементы присутствуют как в одном, так и в другом множестве.
Значение объединения множеств в повседневной жизни
Объединение множеств в математике позволяет нам объединить два или более множества в одно, включая все элементы из каждого множества. Это понятие также находит применение в повседневной жизни, когда мы объединяем разные группы или коллекции в одну.
Например, представьте, что у вас есть две друзьяские группы: одна состоит из ваших школьных друзей, а другая из коллег по работе. Объединение этих двух множеств может помочь вам создать новую, общую группу друзей, где будут представлены и школьные товарищи, и коллеги. Такая новая группа может стать отличным местом для общения и обмена опытом для всех ее членов.
Аналогично, объединение множеств применяется в других ситуациях. Например, при покупке продуктов в супермаркете мы можем объединить множество товаров, которые нужно приобрести, с множеством товаров, которые находятся в нашей корзине. В результате получается общее множество продуктов для покупки.
Также, понятие объединения множеств находит применение в физических тренировках. Если у вас есть две разные программы тренировок - например, оркестрация и силовые упражнения, объединение этих двух множеств может помочь вам создать новую программу тренировок, которая будет включать элементы из каждой программы.
Таким образом, понимание значений и применений объединения множеств в математике может помочь нам не только в учебе, но и в повседневной жизни, где мы можем использовать это понятие для объединения разных групп, коллекций или программ в единое целое.



