Стандарт IEEE 754 определяет представление чисел с плавающей точкой в компьютерах. В этом стандарте числа могут быть представлены в двоичной системе и иметь различные форматы - одиночной (32 бита) и двойной (64 бита) точности. Нормализованное число - это особый формат представления чисел с плавающей точкой, при котором задействуется весь диапазон значений и минимизируется потеря точности.
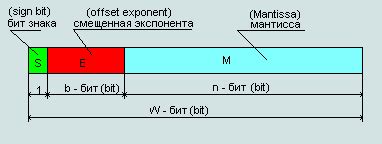
Нормализованное число в стандарте IEEE 754 имеет следующую структуру. В начале числа находится знак - 0 для положительных чисел и 1 для отрицательных. За знаком следует смещенный экспонент, который определяет положение десятичной точки. И наконец, после смещенного экспонента находится мантисса - дробная часть числа, представленная в двоичной системе.
Преимущество нормализованного числа в стандарте IEEE 754 состоит в том, что оно позволяет представить больший диапазон значений с минимальной потерей точности. Благодаря использованию смещенного экспонента и мантиссы с нормализацией, числа с плавающей точкой могут быть более эффективно представлены и использованы в различных приложениях - от научных вычислений до финансовых операций.
Определение нормализованного числа в стандарте IEEE754
В стандарте IEEE 754, нормализованное число определяется как число, представленное в виде дробной части и экспоненты. Это число имеет определенную конкретность и точность.
Нормализованное число в формате IEEE 754 представляется в следующем виде:
- Знак: 1 бит (0 для положительного числа, 1 для отрицательного числа)
- Экспонента: n-битное двоичное целое число, которое определяет положение десятичной точки и диапазон чисел, которые можно представить
- Дробная часть: (n-1)-битное двоичное число, которое определяет мантиссу числа и его точность
При нормализации числа, экспонента находится таким образом, чтобы мантисса была в диапазоне от 1 (включительно) до 2 (не включительно). Такой подход позволяет представить числа с высокой точностью и уменьшить ошибку округления при выполнении арифметических операций.
Нормализованные числа в стандарте IEEE 754 являются чрезвычайно полезными для вычислений, так как они предоставляют механизм точного представления и операций с числами разного масштаба и значения.
Что такое нормализованное число
В представлении числа с плавающей точкой по стандарту IEEE754 используется формат, который состоит из трех частей: знака числа, мантиссы и экспоненты. Нормализованное число представляет собой число, у которого мантисса имеет вид 1.ХХХХХХ, где XXXXXX - шестнадцатеричное число. С помощью нормализованного представления чисел можно увеличить диапазон представимых чисел, минимизировать потерю точности и упростить математические операции с числами.
Нормализованное число в стандарте IEEE754 имеет ноль в старшем бите экспоненты, что позволяет представлять числа с диапазоном экспоненты от -126 до 127 для чисел одинарной точности и от -1022 до 1023 для чисел двойной точности.
| Знак | Экспонента | Мантисса |
|---|---|---|
| 1 бит | 8 бит | 23 бита (для чисел одинарной точности) |
| 1 бит | 11 бит | 52 бита (для чисел двойной точности) |
Стандарт IEEE754 определяет, что нормализованное число принадлежит интервалу от 1.0 до (2-2^(-23)) для чисел одинарной точности и от 1.0 до (2-2^(-52)) для чисел двойной точности.
Стандарт IEEE754
Одной из главных особенностей стандарта IEEE754 является возможность представить числа в нормализованной форме. Нормализованное число представляет собой число, в котором максимальное количество значащих цифр находится перед запятой. Это позволяет повысить точность вычислений и улучшить представление чисел с большим диапазоном значений.
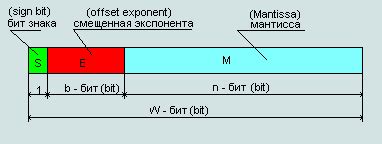
Нормализованное число в стандарте IEEE754 имеет следующую структуру:
- Знак: 1 бит, определяющий знак числа (0 - положительное, 1 - отрицательное).
- Экспонента: разряды, определяющие порядок числа (используется смещенное двоичное представление, чтобы учесть отрицательные значения экспоненты).
- Мантисса: разряды, содержащие значащие цифры числа.
Стандарт IEEE754 также устанавливает правила для выполнения арифметических операций с числами с плавающей точкой, включая сложение, вычитание, умножение и деление. Он также определяет правила округления для получения результатов операций с определенной точностью.
Благодаря стандарту IEEE754 числа с плавающей точкой могут быть представлены и обрабатываться одним общим способом на различных системах и аппаратных платформах, что обеспечивает переносимость и совместимость программного обеспечения.
Представление чисел в формате IEEE754

Стандарт IEEE754 определяет способ представления вещественных чисел в компьютерах. Он используется практически всеми современными компьютерами и программными языками.
В формате IEEE754 числа представляются в виде собственно числа и показателя степени, который определяет положение запятой. Для этого используются различные биты: знаковый бит, биты показателя степени и мантиссы.
Одним из видов представления чисел в формате IEEE754 являются нормализованные числа. Они отличаются от других видов представления тем, что наиболее значимый бит мантиссы всегда равен 1, а показатель степени также может принимать отрицательные значения. Это позволяет представлять числа с большим диапазоном значений и высокой точностью.
Преимущество нормализованных чисел заключается в их удобстве использования и возможности выполнять арифметические операции с высокой точностью. Однако, они требуют больше памяти для хранения и могут вызывать некоторые проблемы с округлением.
В зависимости от размера битового поля показателя степени и мантиссы, форматы представления чисел могут быть разными. Например, стандартный формат для чисел одинарной точности (32 бита) имеет 8 бит для показателя степени и 23 бита для мантиссы, а для чисел двойной точности (64 бита) - 11 бит для показателя степени и 52 бита для мантиссы.
Использование нормализованных чисел в формате IEEE754 позволяет компьютерам и программам работать с вещественными числами с высокой точностью и эффективностью. Однако для представления некоторых особенных значений, таких как бесконечность и NaN (Not-A-Number), используются специальные коды, которые также определены в стандарте.
Различные форматы чисел в стандарте IEEE754
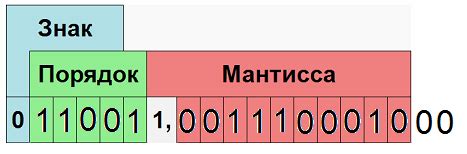
Стандарт IEEE754 определяет формат представления чисел с плавающей точкой, который широко используется в вычислениях на компьютерах. Этот стандарт включает несколько различных форматов чисел, каждый из которых представляет число с разными размерами и диапазонами.
Один из наиболее распространенных форматов в стандарте IEEE754 - это одинарная точность (single precision). В этом формате число представляется 32-битным двоичным числом, которое содержит знак, экспоненту и мантиссу. Этот формат позволяет представлять числа с плавающей точкой в диапазоне от примерно 1.4e-45 до примерно 3.4e38.
Другой распространенный формат - это двойная точность (double precision). В этом формате число представляется 64-битным двоичным числом, также содержащим знак, экспоненту и мантиссу. Формат двойной точности обеспечивает большую точность и диапазон представления чисел, чем одинарная точность. Он позволяет представлять числа с плавающей точкой в диапазоне от примерно 5.0e-324 до примерно 1.8e308.
Кроме того, стандарт IEEE754 также определяет форматы с повышенной точностью (extended precision), которые могут использоваться для более точных вычислений в некоторых приложениях. Форматы с повышенной точностью обычно используют 80 или 128 бит для представления чисел с плавающей точкой, что позволяет получить еще большую точность и диапазон представления чисел.
Выбор формата чисел в стандарте IEEE754 зависит от требуемой точности и диапазона представления чисел в конкретном приложении. Наиболее часто используется формат двойной точности, так как он обеспечивает достаточно высокую точность и диапазон представления чисел для большинства задач.
Преимущества нормализованных чисел
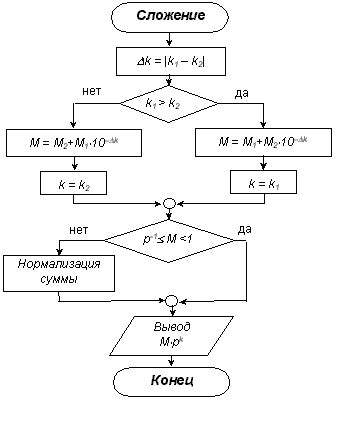
В стандарте IEEE754 нормализованное число представляет собой число, которое имеет максимальную точность представления и минимальную абсолютную погрешность.
Нормализованные числа имеют следующие преимущества:
| Увеличение точности | Нормализованные числа позволяют представлять числа с большей точностью и меньшей погрешностью. Это особенно важно для вычислений, где требуется высокая точность, например, в финансовых расчетах или при работе с большими числами. |
| Облегчение сравнения чисел | Благодаря нормализации чисел, сравнение двух чисел становится проще и надежнее. Это особенно важно при вычислениях с плавающей точкой, где округление может привести к неправильному сравнению чисел. |
| Оптимизация использования памяти | Нормализация позволяет эффективно использовать память, так как она исключает неиспользуемые или избыточные биты. Это особенно важно для систем с ограниченными ресурсами, таких как встроенные системы или мобильные устройства. |
| Уменьшение ошибок округления | Благодаря нормализации чисел, ошибки округления минимизируются, что улучшает точность результатов вычислений. Это особенно важно для приложений, где округление имеет критическое значение, например, при вычислении физических или научных величин. |
Нормализованные числа являются основой для точных и надежных вычислений с плавающей точкой и обеспечивают сочетание высокой точности, эффективного использования памяти и минимальной погрешности.
Применение нормализованных чисел в вычислениях
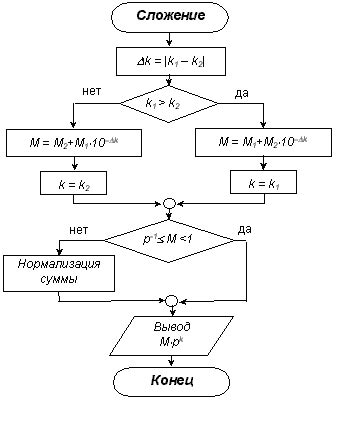
Нормализованные числа, определенные в стандарте ieee754, широко применяются в вычислениях, особенно в сферах, где точность и скорость играют важную роль.
Когда числа нормализуются, они приводятся к такому формату, где старший бит всегда равен 1. Это позволяет использовать полный диапазон значений, избегая потерь точности и увеличивая диапазон чисел, которые можно представить в данном формате.
В вычислительной технике нормализованные числа позволяют эффективно и точно выполнять арифметические операции, такие как сложение, вычитание, умножение и деление. Благодаря нормализации чисел, можно избежать ошибок округления и потери точности, что особенно важно в научных вычислениях и обработке сигналов.
Применение нормализованных чисел также позволяет снизить потребление памяти и увеличить быстродействие вычислительных алгоритмов. Это особенно актуально для приложений, работающих с большими объемами данных, таких как геоинформационные системы, компьютерное зрение и искусственный интеллект.



