Мода и медиана - это статистические показатели, которые используются для анализа данных в алгебре. Они помогают определить характеристики набора чисел, такие как типичное значение и наиболее часто встречающееся значение.
Мода представляет собой значение или значения, которые встречаются наиболее часто в данном наборе чисел. Другими словами, это число или числа, которые имеют наибольшую частоту встречаемости. Например, если у нас есть набор чисел: 2, 3, 4, 4, 5, 6, 6, то мода этого набора будет 4 и 6, так как они встречаются дважды, в то время как остальные числа встречаются только один раз.
Медиана - это значение, которое находится в середине набора чисел после их упорядочивания по возрастанию или убыванию. Если у нас есть набор чисел: 1, 2, 3, 4, 5, то медианой этого набора будет значение 3, так как оно находится в середине после упорядочивания чисел.
Использование моды и медианы в алгебре может быть полезным для анализа данных, проведения исследования или принятия решений на основе числовой информации. Эти показатели позволяют определить наиболее типичное значение и центральную точку набора чисел, что может быть полезно для деловых и научных целей.
Мода и медиана в алгебре: основные понятия и их различия

Мода в алгебре относится к значению или значениям, которые встречаются наиболее часто в наборе данных. Другими словами, мода представляет собой самую популярную или наиболее частую величину в наборе. Если в наборе есть две или более часто встречающихся значений, то говорят о мультимодальном распределении.
Медиана, с другой стороны, является значением, которое разделяет набор данных на две равные части. Для нахождения медианы необходимо упорядочить данные по возрастанию или убыванию и выбрать среднее значение. Если в наборе данных нечетное количество элементов, медиана является серединным значением. В случае четного количества элементов медиану находят как среднее арифметическое двух соседних значений в середине набора.
Основное отличие между модой и медианой заключается в том, что мода отражает наиболее часто встречающиеся значения в наборе данных, в то время как медиана демонстрирует среднее значение, которое разделяет данные на две равные части. Фактически, мода относится к порядку чисел, а медиана - к центральному положению. Эти два статистических показателя полезны для изучения формы и характеристик набора данных, и их использование в алгебре позволяет получить более полное представление о значениях в наборе.
Определение моды и медианы
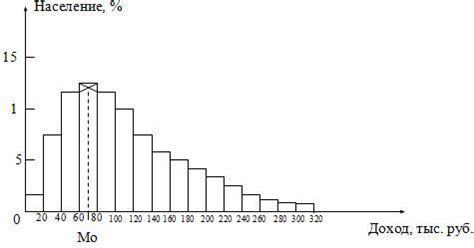
Мода - это значение или значения, которые встречаются наиболее часто в наборе чисел. Другими словами, это самое популярное значение или значения в наборе. Если мода единственная, то набор чисел называется унимодальным. Если мода несколько, то набор чисел называется мультимодальным. Если ни одно значение не повторяется, то набор чисел не имеет моды.
Медиана - это значение, которое разделяет набор чисел на две равные части. Другими словами, это значение, которое находится в середине упорядоченного набора чисел. Чтобы найти медиану, нужно упорядочить числа по возрастанию или убыванию и выбрать значение, которое находится посередине. Если набор чисел содержит нечетное количество элементов, медиана будет являться единственным значением. Если количество элементов четное, медиана будет средним значением двух соседних чисел.
Мода и медиана позволяют нам получить представление о типичных значениях в наборе чисел. Мода предоставляет информацию о том, какое значение встречается наиболее часто, а медиана показывает нам центральное значение. Использование моды и медианы может быть полезным при анализе данных и принятии решений.
Формула расчета моды
| Шаг | Формула |
|---|---|
| 1 | Упорядочите набор данных по возрастанию или убыванию. |
| 2 | Посчитайте частоту появления каждого значения в наборе данных. |
| 3 | Выберите значение с наибольшей частотой - это и будет мода. |
Например, рассмотрим следующий набор данных: 2, 3, 4, 4, 5, 5, 5, 6, 7. После упорядочивания данных по возрастанию получим: 2, 3, 4, 4, 5, 5, 5, 6, 7. Затем посчитаем частоту появления каждого значения: 2 - 1 раз, 3 - 1 раз, 4 - 2 раза, 5 - 3 раза, 6 - 1 раз, 7 - 1 раз. Самое часто встречающееся значение - 5, поэтому мода в данном наборе данных равна 5.
Формула расчета моды позволяет нам определить наиболее типичное значение в наборе данных и использовать его для различных статистических анализов.
Формула расчета медианы

Формула расчета медианы зависит от количества значений в наборе данных:
Если количество значений нечетное:
медиана = значение в середине упорядоченного ряда
Например, если у нас есть набор данных: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Значение в середине упорядоченного ряда составляет 5, поэтому медиана равна 5.
Если количество значений четное:
медиана = среднее арифметическое двух значений в середине
Например, если у нас есть набор данных: 1, 2, 3, 4, 5, 6, 7, 8.
Значения в середине упорядоченного ряда - 4 и 5. Среднее арифметическое этих двух значений составляет 4.5, поэтому медиана равна 4.5.
Формула расчета медианы позволяет нам определить центральное значение в наборе данных и найти характеристику, которая не зависит от выбросов или экстремальных значений.
Мода и медиана: примеры применения

Применение моды и медианы может быть полезным в различных областях.
Пример 1: Зарплата сотрудников
Представим, что у нас есть набор данных, состоящий из зарплат сотрудников в компании. Используя моду, мы можем определить самую распространенную зарплату компании, которая может быть полезной при разработке бюджета и планировании затрат. Медиана, с другой стороны, позволяет определить среднюю зарплату в компании и сравнить ее с модой, чтобы получить более полное представление о зарплатной структуре.
Пример 2: Оценки студентов
В образовательной сфере мода и медиана также могут быть полезными инструментами. Например, мода может помочь выявить наиболее часто встречающиеся оценки по предмету, что может помочь преподавателям понять, какие темы или концепции вызывают наибольшие трудности у студентов. Медиана, с другой стороны, позволит определить среднюю оценку по предмету и выявить возможные выбросы или аномалии.
Пример 3: Продажи товаров
Другой пример применения моды и медианы - анализ продаж товаров компании. Мода позволяет определить самые популярные товары, что может быть полезным при планировании производства или закупке товаров. Медиана, с другой стороны, помогает выявить средние продажи и оценить общую прибыльность товаров.
Примеры применения моды и медианы могут быть разнообразными, и в каждом конкретном случае эти статистические показатели могут дать полезную информацию для принятия решений и анализа данных.
Различия между модой и медианой
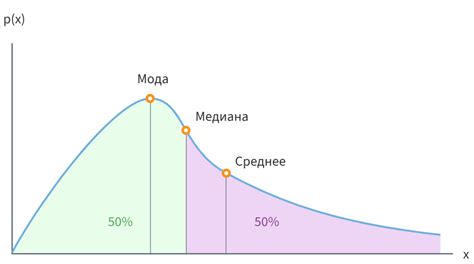
Мода - это значение или значения, которые наиболее часто встречаются в выборке или наборе данных. Она показывает наиболее типичное значение в наборе данных и используется в основном для категориальных переменных. Если в выборке есть несколько значений, которые встречаются одинаковое количество раз и наибольшее, то таких значений может быть несколько. В этом случае говорят, что выборка имеет модальность больше одного значения.
Медиана - это значение, которое делит упорядоченные данные на две равные части. То есть половина значений находится выше медианы, а половина - ниже. Медиана используется в основном для непрерывных и упорядоченных переменных. Если в выборке имеется четное количество значение, то медианой будет являться среднее арифметическое двух средних значений.
Основное различие между модой и медианой заключается в том, что мода определяет наиболее часто встречающееся значение или значения в наборе данных, в то время как медиана определяет центральное значение, которое разделяет данные на две равные части.
Преимущество использования моды заключается в том, что она может применяться ко всем типам данных, включая категориальные переменные. Кроме того, мода более устойчива к выбросам или экстремальным значениям в выборке, чем медиана.
С другой стороны, медиана предоставляет более надежную оценку центральной тенденции, особенно когда выборка содержит выбросы или экстремальные значения. Она также может быть полезна, когда данные не имеют условной шкалы или отсутствуют точные численные измерения.
В зависимости от конкретной задачи или типа данных, мода и медиана могут предоставить дополнительную информацию о наборе данных и помочь в анализе и интерпретации результатов.
Зависимость моды и медианы от выбросов
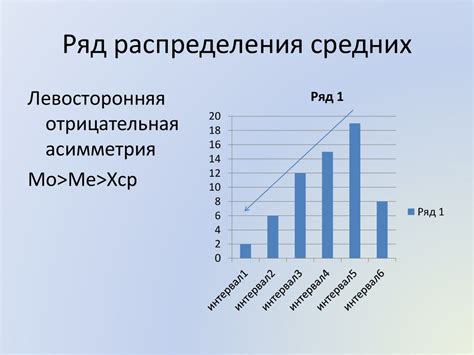
Выбросы - это значения, которые существенно отличаются от остальных данных. Они могут возникать из-за ошибок в измерениях или быть результатом реальных аномалий в данных. Когда в наборе данных присутствуют выбросы, медиана и мода могут показать нам не типичное значение общей выборки, а значение, отражающее выброс. В таком случае, эти меры центральной тенденции могут оказаться не репрезентативными для общего набора данных.
Медиана - это значение, которое разделяет упорядоченный набор данных на две равные части. Если в наборе данных есть выбросы, эти значения могут существенно изменить медиану. Особенно если выброс соответствует значению, которое является очень большим или очень маленьким по сравнению с остальными данными. В этом случае медиана будет сдвинута в направлении значения выброса.
Мода - это значение, которое встречается наиболее часто в наборе данных. Если в наборе данных есть выбросы, то мода может быть искажена. Например, если в наборе данных есть несколько выбросов, которые отличаются от остальных, модой может стать какое-либо из этих значений выбросов.
Итак, при анализе данных важно учитывать наличие выбросов и применять дополнительные методы для оценки центральной тенденции, которые устойчивы к выбросам. Например, среднее значение может использоваться вместо медианы в случае, когда выбросы существенно искажают результаты. Также можно применять робастные методы оценки центральной тенденции, которые предназначены специально для работы с выбросами.
Важность определения моды и медианы в алгебре

Мода - это значение или значения, которые встречаются наиболее часто в наборе данных. Определение моды позволяет нам выявить наиболее типичные или наиболее часто встречающиеся значения в выборке. Это полезно для понимания основных характеристик данных и их распределения. Например, если мы исследуем результаты экзамена в классе, мода поможет нам определить, какая оценка является наиболее типичной.
Медиана - это среднее значение в упорядоченном по возрастанию или убыванию ряду данных. Определение медианы позволяет нам найти центральное значение в выборке. Это особенно полезно, когда данные несимметрично распределены или содержат выбросы. Например, если мы анализируем доходы сотрудников в компании, медиана может дать нам более репрезентативное представление о среднем доходе, чем общее среднее значение.
Понимание моды и медианы помогает нам анализировать и интерпретировать данные более точно и полно. Они предоставляют нам дополнительные инструменты для оценки распределения и характеристик данных. Поэтому, при работе с числовыми значениями в алгебре, определение моды и медианы является важным шагом для более глубокого и точного понимания данных.
Роль моды и медианы в статистическом анализе
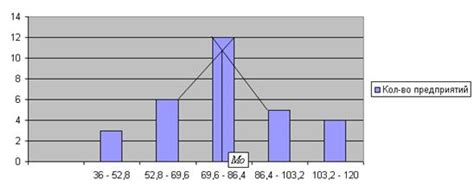
Мода
Мода представляет собой значение или значения в наборе данных, которые встречаются наиболее часто. Если в наборе данных есть одна мода, то его называют унимодальным распределением. Если есть несколько мод, то это будет мультимодальное распределение. Если все значения в наборе данных встречаются одинаковое количество раз, то распределение называется безмодальным.
Мода может быть полезна, когда мы хотим найти наиболее типичное или наиболее часто встречающееся значение в наборе данных. Она может быть использована для определения модных тенденций, предпочтений и популярных закономерностей в различных областях, таких как мода, экономика и маркетинг.
Медиана
Медиана представляет собой значение, которое разделяет набор данных на две равные половины: половину значений, которые меньше медианы, и половину значений, которые больше медианы. Если количество значений в наборе данных нечетное, то медиана будет точным значением. Если количество значений четное, то медиана будет средним значением двух средних чисел.
Медиана полезна, когда у нас есть выбросы или сильно искаженные данные, которые могут влиять на среднее значение данных. В отличие от среднего значения, медиана не чувствительна к экстремальным значениям. Она обеспечивает более устойчивую меру центральной тенденции и может быть использована для оценки типичных значений в наборе данных.



