Математика - это наука о числах и их взаимоотношениях. Она имеет множество терминов и понятий, которые помогают нам понять мир вокруг нас. Одним из основных понятий в математике является понятие множителя и произведения.
Множитель - это число, на которое производится умножение. Он является одним из двух элементов в математической операции умножения, второй элемент называется другим множителем. Вместе они образуют произведение, которое является результатом умножения двух чисел.
Произведение - это результат умножения двух или более чисел. Оно выражается в виде числа, полученного умножением множителей. Произведение является основной операцией в арифметике и играет важную роль в решении различных математических проблем.
Например, если у нас есть два множителя - 3 и 4, и мы их умножим, то получим произведение 12.
Операция умножения имеет свои особенности и правила, которые позволяют правильно выполнять эту операцию с различными числами.
Теперь, когда мы знаем, что такое множитель и произведение, мы можем легче понять и решать математические задачи, связанные с умножением.
Множитель и произведение: основные понятия
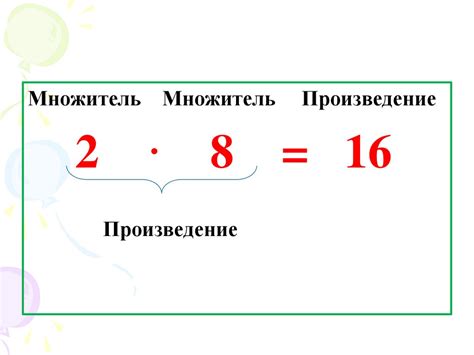
Множитель - это число или выражение, участвующее в умножении. Оно может быть представлено как одно число, так и сложное выражение, состоящее из нескольких чисел или переменных, объединенных операцией умножения. Множители могут быть целыми или дробными числами, а также переменными или алгебраическими выражениями.
Произведение - это результат умножения двух или более множителей. Оно также может быть представлено как число или выражение, в зависимости от характера и типа множителей. При умножении, каждый множитель умножается на другие множители, и все полученные произведения складываются вместе для получения окончательного значения произведения.
Умножение и понимание множителя и произведения является важной частью математической основы. Эти понятия позволяют решать различные задачи, проводить дальнейшие вычисления и применять математические операции в повседневной жизни и в различных областях науки и техники.
Что такое множитель в математике и как он работает?

В умножении, множитель - это число или выражение, которое умножается на другое число или выражение, называемое другим множителем. Множители вместе образуют произведение.
Примером может служить умножение двух чисел. Например, умножение числа 4 на число 5:
- Первый множитель: 4
- Второй множитель: 5
- Произведение: 20
В этом примере, число 4 является первым множителем, а число 5 - вторым множителем. Умножив их вместе, получим произведение, равное 20.
Множители можно задавать не только числами, но и выражениями. Например, при умножении 2 на (x + 3), первым множителем является число 2, а вторым множителем - выражение (x + 3). При умножении этих множителей, получим произведение, которое зависит от переменной x.
Важно помнить, что порядок множителей в умножении может быть изменен, и произведение будет оставаться неизменным. Также можно умножать более чем два множителя, просто добавляя их в последовательность умножения.
Множитель - это ключевое понятие в математике и находит широкое применение в различных областях, таких как алгебра, геометрия и физика. Понимание множителя и его роли в умножении является важным фундаментом для изучения более сложных математических концепций.
Произведение чисел: базовая информация
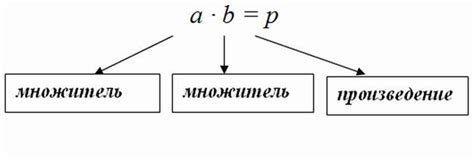
Множество чисел, участвующих в произведении, называется множителями. Число, которое получается в результате умножения, называется произведением.
Произведение обозначается символом "×" или "*", где числа, подлежащие умножению, записываются через этот символ. Например, произведение чисел 3 и 5 можно записать как 3 × 5 или 3 * 5.
Произведение чисел имеет несколько особенностей:
| Пример | Результат |
|---|---|
| 3 × 4 | 12 |
| 5 × 0 | 0 |
| (-2) × (-6) | 12 |
| 8 × 1 | 8 |
В первом примере произведение чисел 3 и 4 равно 12. Во втором примере, когда один из множителей равен нулю, произведение будет равно нулю. В третьем примере, произведение двух отрицательных чисел дает положительный результат. В последнем примере, произведение числа на единицу не меняет число.
Произведение чисел играет важную роль во многих областях математики, физики, экономики и других науках. Оно позволяет решать различные задачи и применяется в различных математических моделях и формулах.
Зачем нужно знать понятие произведения и множителя в математике?

Произведение - это результат умножения двух или более чисел. Оно обозначается знаком умножения (×) или точкой (·). Например, произведение чисел 3 и 4 равно 12: 3 × 4 = 12. Произведение может быть положительным, отрицательным или нулем, в зависимости от знаков множителей.
Множитель - это числа, которые участвуют в умножении, то есть числа, которые перемножаются. Если у нас есть произведение 3 × 4 = 12, то числа 3 и 4 являются множителями. Они определяют размер и характеристики произведения.
Знание понятий произведения и множителя позволяет нам решать различные задачи, связанные с умножением. Например, они помогают нам расчитать площадь прямоугольника, длину или ширину отрезка, количество предметов в группе и т.д.
Также знание произведения и множителя позволяет нам лучше понимать алгебраические выражения, раскрывать скобки и упрощать сложные выражения. Они являются основой для изучения более сложных понятий в математике, таких как степень, корень, функции и другие.
Итак, понятие произведения и множителя в математике играет важную роль, позволяя нам решать различные задачи и строить более сложные математические модели. Поэтому знание и понимание этих понятий является необходимым для развития математической грамотности и применения ее в реальной жизни.
Как применяются произведение и множитель в реальной жизни?

Одна из областей, где произведение и множитель играют важную роль, – это финансы. Например, при расчете общей стоимости товара, нужно умножить его цену на количество единиц. Множитель в данном случае будет представлять количество товара, а произведение покажет общую стоимость покупки.
В инженерии произведение и множитель могут использоваться для вычисления площади, объема, мощности и других физических характеристик. Например, чтобы найти площадь прямоугольника, нужно умножить длину на ширину, где длина и ширина будут множителями, а произведение покажет площадь.
В науке произведение и множитель используются для выполнения различных вычислений и измерений. Например, в физике, чтобы найти работу, нужно умножить силу на расстояние, по которому она действует. В этом случае сила и расстояние будут множителями, а произведение выразит совершенную работу.
Важно отметить, что произведение и множитель могут применяться во многих других областях, включая бизнес, экономику, программирование и т. д. Они помогают в анализе данных, предсказании трендов и решении различных задач.



