Что такое медиана треугольника и как она связана с его сторонами и вершинами?

В геометрии медиана треугольника является одной из важных характеристик этой фигуры. Медиана - это отрезок, соединяющий одну вершину треугольника с серединой противоположной стороны. Таким образом, каждый треугольник имеет три медианы, которые пересекаются в одной точке, называемой центром масс или центроидом.

Медианы треугольника являются очень важными в геометрии и имеют множество интересных свойств. Они делятся в отношении 2:1, то есть, каждая медиана делит противоположную сторону на две части, при этом более длинная часть соответствует двум более коротким частям вместе взятым. Это очень полезное свойство, которое находит применение при решении различных задач на планиметрию.

Медианы треугольника также помогают определять некоторые важные характеристики фигуры: они равны половине длины основания призмы треугольной формы, а также являются высотами и биссектрисами треугольника. Кроме того, медианы делят площадь треугольника на шесть равных частей, что также позволяет находить площадь различных фигур, основанных на треугольниках.

Медиана треугольника - определение и основные свойства

Главное свойство медианы треугольника заключается в том, что она делит каждую сторону на две равные части. То есть, медиана является линией, проходящей через точку, делящую сторону треугольника пополам.

Основные свойства медианы треугольника включают:

1. Медианы треугольника пересекаются в одной точке, называемой центром тяжести треугольника.
2. Центр тяжести треугольника делит каждую медиану в отношении 2:1. То есть, расстояние от начала медианы до центра тяжести в два раза больше, чем расстояние от центра тяжести до конца медианы.
3. Медианы треугольника являются осью симметрии. Если провести симметричные отрезки от вершин треугольника до точек пересечения медиан, то они будут равны и пересекаться в точке, лежащей на оси симметрии - центре тяжести треугольника.
4. Площадь каждого из трех треугольников, образованных сторонами треугольника и медианами, равна четверти площади исходного треугольника.

Медианы треугольника являются важным элементом в геометрии. Они имеют много применений, включая вычисление центра тяжести, определение точек пересечения линий и оценку площадей треугольников.

Определение медианы треугольника

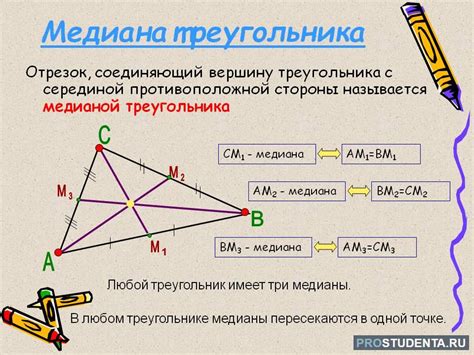
Для того чтобы найти медиану треугольника, необходимо взять одну из его вершин и провести от нее линию через середину противоположной стороны. В результате мы получим отрезок, который и будет медианой. Отметим, что треугольник может иметь три медианы, каждая из которых соединяет одну из вершин с серединой противоположной стороны.

Медианы треугольника имеют ряд интересных свойств и важную геометрическую роль. Например, точка пересечения всех трех медиан называется центром тяжести треугольника. Этот центр является точкой, в которой сосредоточена основная масса треугольника. Кроме того, медианы делятся этим центром на три равных отрезка.

Медиана также служит опорой для серединного перпендикуляра, проходящего через середину стороны треугольника. Серединный перпендикуляр равноудален от концов стороны и перпендикулярен ей. Кроме того, каждая из трех медиан является биссектрисой угла, образованного этой медианой и соответствующей стороной треугольника.

Свойства медианы треугольника

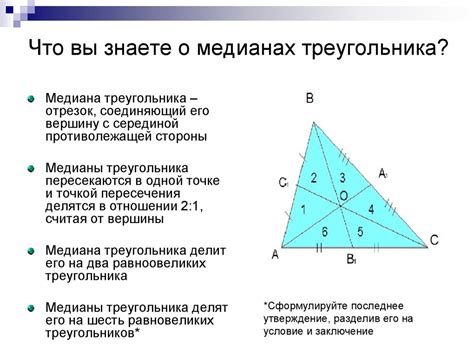
• Медианы пересекаются в одной точке, которая называется центром тяжести треугольника. Это важное свойство, которое позволяет находить и изучать различные характеристики треугольников.
• Медиана делит каждую сторону треугольника на две равные части. Точка пересечения медиан и сторон называется точкой деления и является серединой этой стороны.
• Длина медианы равна половине суммы длин оставшихся двух сторон треугольника. Например, если длины сторон треугольника равны a, b и c, то длина медианы, проведенной из вершины, противоположной стороне длиной c, равна √(2b^2 + 2a^2 - c^2)/2.
• Медианы разделяют площадь треугольника на шесть равных треугольников.

Свойства медианы треугольника используются в различных областях геометрии, физики и инженерии для решения задач и нахождения различных характеристик треугольников.

Медианы и центр тяжести треугольника

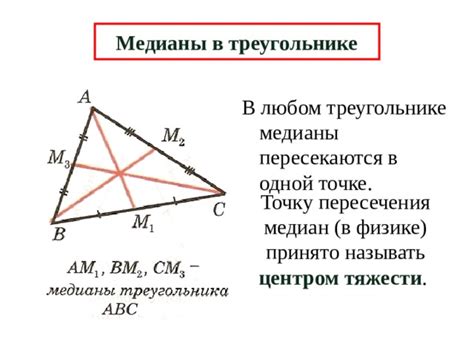
Медианы треугольника делятся в отношении 1:2. То есть, если обозначить середину стороны треугольника точкой M, а вершину – точкой A, то отрезок AM составляет 1/3 длины медианы, а отрезок M до середины противоположной стороны – 2/3 длины медианы.

Центр тяжести треугольника обладает следующими свойствами:

• Соотношение площадей: Центр тяжести треугольника делит медианы в отношении 2:1. Это значит, что площадь треугольника, образованная центром тяжести и двумя его вершинами, в два раза меньше, чем площадь всего треугольника.
• Стабильность: Центр тяжести треугольника стабильный и не зависит от формы и размера треугольника. Он всегда находится внутри треугольника и является точкой пересечения медиан.
• Значение в геометрии: Медианы и центр тяжести треугольника широко используются в геометрии для решения различных задач и построений.

Стороны и медианы треугольника

Медиана треугольника - это отрезок, соединяющий одну вершину треугольника с серединой противоположной стороны. Каждый треугольник имеет три медианы, и все три медианы пересекаются в одной точке, называемой центром масс треугольника или центром треугольника. Центр треугольника дели

Применение медиан треугольника в практике

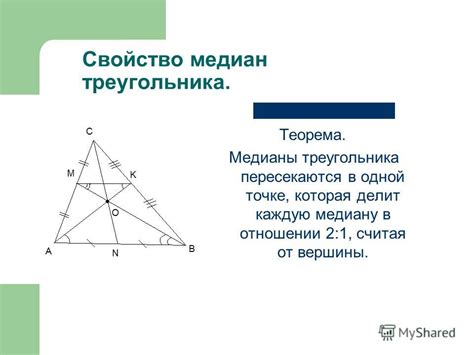
Медианы треугольника играют важную роль в геометрии и находят свое применение в различных практических задачах. Ниже приведены некоторые примеры использования медиан треугольника:

1. Определение центра тяжести. Медианы треугольника пересекаются в одной точке, называемой центром тяжести. Эта точка является барицентром или "средней точкой" треугольника. Она имеет свойство разделять каждую медиану в отношении 2:1. Центр тяжести применяется в различных областях, включая архитектуру, инженерное дело и дизайн.
2. Определение высоты треугольника. Медиана треугольника, проведенная из вершины до середины противоположной стороны, является высотой этого треугольника. Определение высоты позволяет расчетать площадь треугольника, а также может быть использовано в проектировании наклонных крыш и других конструкций.
3. Нахождение точки пересечения медиан. Точка пересечения всех медиан треугольника называется центром окружности, вписанной в треугольник. Эта точка имеет равное расстояние до всех вершин треугольника и является центром окружности, которая касается всех сторон треугольника. Нахождение этой точки может быть полезно при решении различных задач в триангуляции или построении окружностей.

Таким образом, медианы треугольника имеют важное практическое значение, не только в геометрии, но и в разных областях человеческой деятельности. Их применение помогает в решении разнообразных задач конструирования, проектирования и расчета площадей.

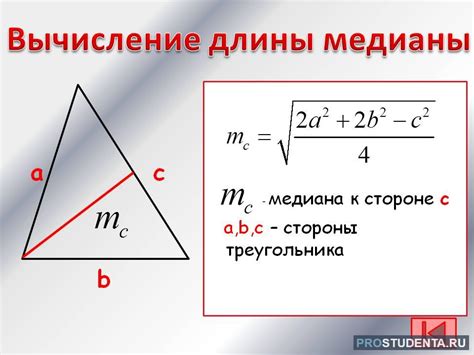
Формула вычисления длины медианы треугольника

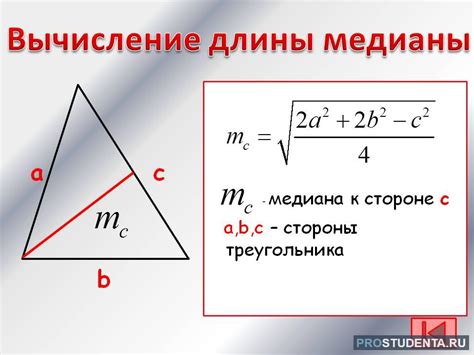
Медиана = (1/2) * √(2 * a² + 2 * b² - c²)

Где a, b и c - длины сторон треугольника.

Формула основана на теореме о медиане треугольника. Для ее применения необходимо знать длины всех сторон треугольника. Подставив значения сторон в формулу, можно легко вычислить длину медианы.

Медианы являются важным инструментом в геометрии и находят применение при решении различных задач. Они делят треугольник на три равные части и пересекаются в точке, называемой центром медиан.

Примеры решения задач с медианой треугольника

Рассмотрим несколько примеров задач, в которых необходимо использовать медиану треугольника:

Пример 1:

Дан треугольник ABC, в котором AC = 6 см, BC = 8 см и медиана AM делит сторону BC пополам. Найдите длину отрезка BM.

Решение:

Так как медиана AM делит сторону BC пополам, то BM = MC. Используем теорему Пифагора для нахождения длины стороны BM:

BM² = AB² - AM²

По формуле Пифагора, AB² = AC² + BC²:

BM² = AC² + BC² - AM²

Подставляем известные значения:

BM² = 6² + 8² - (1/2 BC)²

Вычисляем:

BM² = 36 + 64 - (1/4 BC²)

BM² = 100 - (1/4 BC²)

BM = 10 см.

Пример 2:

Дан треугольник ABC, в котором AB = 5 см, BC = 6 см и медиана AM делит сторону BC в отношении 1:2. Найдите длину отрезка BM.

Решение:

Пусть BM = x, тогда MC = 2x. Используем теорему Пифагора для нахождения длины стороны BM:

BM² = AB² - AM²

По формуле Пифагора, AB² = AC² + BC²:

(3x)² = 6² + 5² - (2x)²

9x² = 36 + 25 - 4x²

13x² = 61

x² ≈ 4.69

x ≈ 2.16

BM ≈ 2.16 см.

Таким образом, длина отрезка BM составляет примерно 2.16 см.