Луч – это особая геометрическая фигура, которая имеет начальную точку и простирается бесконечно в одном направлении. Луч можно представить себе как стрелку, которая начинается в определенной точке и направлена вдоль прямой. Важно отметить, что луч не имеет конечной длины, он продолжается в бесконечность.
Прямая – это другая геометрическая фигура, которая не имеет ни начала, ни конца. Она представляет собой ровный отрезок, который простирается в обе стороны до бесконечности. Прямая всегда находится в одной плоскости и не имеет никаких изгибов или углов.
Разница между лучом и прямой заключается в том, что луч имеет начальную точку и продолжается только в одном направлении, в то время как прямая не имеет начала и конца и простирается в обе стороны. Использование лучей и прямых помогает ученикам лучше понять геометрию и ее основные понятия. Например, лучи могут использоваться для измерения углов, а прямые – для построения геометрических фигур и нахождения центра симметрии.
Определение луча
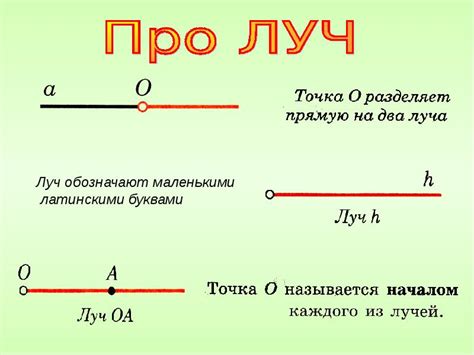
Луч можно представить себе как линию, которая уходит от начальной точки и не имеет конца. Таким образом, луч продолжается бесконечно далеко только в одном направлении, и это отличает его от прямой, которая имеет два конца.
В геометрии лучи часто используются для построения углов и определения положения точек относительно других объектов. Например, угол можно построить, используя два луча, которые имеют общее начало.
Лучи также используются для обозначения линейных составляющих, таких как луч света, который распространяется в пространстве или луч электронов, который имеет определенное направление движения.
Обозначение луча в геометрии делается с помощью двух точек. Первая точка указывает начало луча, а вторая точка указывает направление луча. Например, луч AB обозначает луч, который начинается в точке A и направлен в сторону точки B.
Понятие луча в математике

Начальная точка луча называется его началом, а направление определяется движением от начала луча. Луч не имеет конечной точки и продолжается бесконечно в одном направлении.
Лучи часто используются для обозначения направлений, излучения света или других видов лучей. Например, в геометрии лучи используются для построения углов и определения направлений от точек. Они также могут использоваться для обозначения движения частиц или линий в физике и других науках.
Свойства луча

У луча есть следующие свойства:
- Луч имеет начальную точку, которую обозначают буквой A.
- Луч продолжается в одном направлении, не имея конца.
- Луч можно разделить на две части: первую часть от начальной точки до другой точки, которую обозначают буквой B, и вторую часть, которая продолжается бесконечно.
- Каждый луч имеет имя, которое образуется из трех букв: начальной точки, другой точки и точки, лежащей на луче. Например, если начальная точка луча - A, другая точка - B, и точка, лежащая на луче - C, то луч будет называться лучом AC.
Определение прямой
Прямая в пространстве представляет собой плоскость, а прямая на плоскости представляет собой сплошную линию.
У прямой нет ширины и толщины, она представляет собой только одну размерность - длину.
Прямая может быть определена двумя точками, принадлежащими ей. Существует только одна прямая, которая проходит через две заданные точки.
Прямая может быть прямой линией, а может быть наклонной или горизонтальной, в зависимости от угла, который образует с другими объектами.
| Понятие | Описание |
| Прямая линия | Прямая, которая идет без перегибов и изменения трассы. |
| Наклонная прямая | Прямая, которая образует угол с горизонтальной плоскостью или вертикальной плоскостью. |
| Горизонтальная прямая | Прямая, которая параллельна горизонтальной плоскости и имеет угол 0 градусов с горизонтальной осью координат. |
Понятие прямой в геометрии

Прямую можно представить в виде бесконечно длинной линии, которая состоит из бесконечного числа точек, лежащих по прямой.
Прямая может быть задана двумя точками. Любые две различные точки на прямой могут служить начальной и конечной точкой отрезка, положительно ориентированного от первой точки ко второй.
Прямая - один из основных объектов геометрии и широко применяется для описания отрезков, углов, многоугольников и других фигур.
Свойства прямой

У прямой есть несколько свойств:
- Прямая разделяет плоскость на две части. Любая точка на прямой разделяет плоскость на две полуплоскости: одну справа и одну слева от нее.
- Прямая лежит в одной плоскости. Это означает, что все точки прямой находятся в одной плоскости.
- Прямая наклонна или горизонтальна. Прямая называется наклонной, если она не параллельна ни одной из осей координат и образует угол с ними. Если прямая параллельна оси OX или OY, то она называется горизонтальной.
- Прямая пересекает другие прямые и отрезки. В зависимости от своего положения и угла наклона прямая может пересекать другие прямые и отрезки либо не пересекать их.
Изучение свойств прямых поможет нам правильно понять и использовать их в геометрических задачах и конструкциях.



