Геометрия – это одна из важных разделов математики, которая изучает пространственные объекты и их свойства. В школьной программе геометрию изучают начиная с 7 класса, когда дети уже обладают достаточной математической базой и могут более углубленно изучать геометрические понятия.
Одним из учебников, который пользуется большим спросом у учеников и учителей, является учебник "Луч геометрия 7 класс" Ф.Г. Атанасяна. В этом учебнике собраны все основные понятия, правила и задачи, которые необходимо знать и уметь решать на уроках геометрии в 7 классе. Он составлен таким образом, что каждый ученик сможет легко освоить материал и успешно применить его на практике.
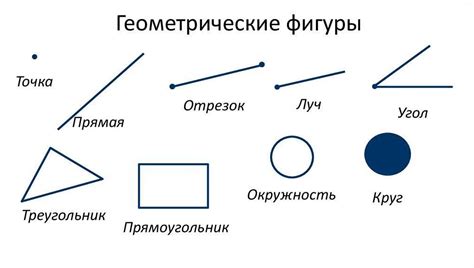
В учебнике "Луч геометрия 7 класс" Ф.Г. Атанасяна разбираются такие важные понятия, как прямая и плоскость, угол и треугольник, круг и окружность. Учащиеся узнают основные свойства и правила нахождения периметра и площади этих геометрических фигур, а также научатся решать задачи, связанные с ними.
Луч геометрия 7 класс: предмет изучения и основные понятия

Луч – это часть прямой, имеющая начальную точку и неограниченно продолжающаяся в одном направлении. Начальная точка луча называется его началом, а направление продолжения – его направлением. Отличительной особенностью луча является то, что он имеет только одну начальную точку.
Луч обозначается символом “→” с двумя точками, одна из которых является его началом. Например, луч АВ можно обозначить как А→В.
Лучи бывают разных видов, в зависимости от их положения и направления. Например, лучи могут быть вертикальными, горизонтальными или наклонными.
Изучение лучей в геометрии 7 класса позволяет понять и использовать основные правила и свойства лучей для решения геометрических задач. Например, можно определить пересечение лучей, построить параллельные и перпендикулярные лучи, а также использовать лучи для построения геометрических фигур.
Луч: определение и свойства
Основные свойства луча:
- Луч не имеет конца в противоположном направлении и продолжается бесконечно в этом направлении.
- Луч может пересекать прямые и плоскости, а также может быть пересечен ими.
- Луч не имеет ширины, а только длину.
- Луч может быть отрицательным, если указывает в обратную сторону.
- Лучи могут быть параллельными, если имеют одно и то же направление.
Изучение лучей является важным элементом геометрии, так как позволяет решить множество задач, связанных с прямыми и плоскостями.
Угол: классификация и измерение

Классификация углов основывается на их величине:
- Острый угол - угол, меньше прямого угла (меньше 90 градусов).
- Прямой угол - угол, равный 90 градусам.
- Тупой угол - угол, больше прямого угла и меньше 180 градусов.
- Разносторонний угол - угол, все стороны которого имеют разную длину.
- Равнобедренный угол - угол, у которого две стороны имеют одинаковую длину.
- Равносторонний угол - угол, у которого все три стороны имеют одинаковую длину.
Измерение углов производится в градусах. Градус измерения угла относится к целому количеству равных частей, на которые можно разделить полный угол (360 градусов). Также используются минуты и секунды для более точного измерения, где 1 градус равен 60 минутам, а 1 минута равна 60 секундам.
Определение положения двух лучей и их связь с углами
Если два луча имеют общую начальную точку и не пересекаются, то они называются смежными. Смежные лучи образуют пару противолежащих углов, у которых стороны являются лучами.
Если два луча имеют общую начальную точку и пересекаются, то они называются взаимоположенными. Взаимоположенные лучи также образуют пары противолежащих углов, у которых стороны являются лучами.
Для указания положения двух лучей относительно друг друга, используются такие термины как "лежит между", "расположен с одной стороны" и "расположен с противоположных сторон".
Отрезок и луч: различия и связь
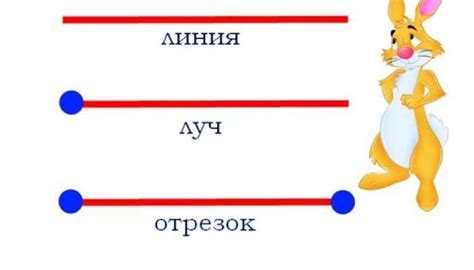
Отрезок - это часть прямой, ограниченная двумя точками, которые называются концами отрезка. Отрезок обозначается двумя точками, находящимися на его концах. Например, AB - отрезок, состоящий из точек A и B.
Луч - это часть прямой, которая имеет начальную точку и простирается бесконечно в одном направлении. Луч обозначается начальной точкой и любой другой точкой, находящейся на нем. Например, AB - луч, начинающийся в точке A и простирающийся бесконечно в направлении точки B.
Таким образом, основное различие между отрезком и лучом заключается в том, что отрезок имеет два конца и ограничен определенным участком прямой, в то время как луч имеет только начальную точку и простирается бесконечно в одном направлении.
Отрезок и луч связаны между собой, поскольку любой отрезок можно продолжить до луча, добавив к нему бесконечно удаленные отрезок конечным и бесконечным участком. Например, отрезок AB можно продолжить до луча AB, который будет простираваться бесконечно в направлении точки B.
Имея понимание отрезков и лучей, мы можем выполнять различные геометрические операции, такие как измерение длины отрезка, построение луча, определение взаимного расположения отрезков и лучей и многое другое.
Правила работы с лучами и углами по методу Ф.Г. Атанасяна
Луч - это часть прямой, которая имеет начальную точку и продолжается бесконечно в одном направлении. Лучи обладают несколькими важными свойствами:
| Символ | Обозначение | Описание |
| ↔ | AB | Прямая, содержащая точки A и B |
| → | →AB | Луч, исходящий из точки A и направленный в точку B |
| ← | ←AB | Луч, исходящий из точки B и направленный в точку A |
Угол - это область плоскости, образованная двумя лучами, начало которых совпадает, а направления различны. Углы бывают различных видов:
| Символ | Обозначение | Описание |
| ∠ | ∠A | Угол, образованный лучами, исходящими из точки A |
| ∠BAC | ∠BAC | Угол, заключенный между лучами AB и AC |
| ∠ABC | ∠ABC | Угол, образованный лучами AB и BC |
Правила работы с лучами и углами, предложенные Ф.Г. Атанасяном, помогают решать задачи, связанные с определением взаимного расположения лучей и углов, а также вычислять их значения. Эти правила включают в себя определения, свойства и правила построения лучей и углов.
Знание основных понятий и правил работы с лучами и углами является основой для изучения более сложных геометрических конструкций и доказательств теорем. Поэтому важно уделить достаточно времени изучению и пониманию этих понятий и правил.



