Система уравнений с двумя переменными - это математическая система, состоящая из двух уравнений, в которых неизвестные переменные связаны между собой. Такая система может иметь одно или более решений, а ее решение представляет собой значения переменных, при которых оба уравнения выполняются одновременно.
Решение системы уравнений с двумя переменными может быть найдено с помощью различных методов, таких как графический метод, метод подстановки, метод сложения и вычитания, и другие. Каждый из этих методов имеет свои преимущества и может быть использован в зависимости от конкретной задачи.
Для лучшего понимания системы уравнений с двумя переменными полезно рассмотреть примеры. Один из таких примеров может быть система уравнений:
3x + 2y = 12
4x - y = 6
В этом примере у нас есть два уравнения, в которых присутствуют переменные x и y. Целью является найти значения x и y, при которых оба уравнения выполняются. Для решения этой системы уравнений можно использовать различные методы, например, метод подстановки или метод сложения и вычитания.
Что такое система уравнений с двумя переменными?

Системы уравнений с двумя переменными могут иметь различные виды решений: одно решение, когда существует одна пара значений переменных, удовлетворяющих обоим уравнениям; бесконечное множество решений, когда уравнения эквивалентны или линейно зависимы; или же система может быть несовместной, то есть не иметь решений.
В случае, если система уравнений с двумя переменными имеет решение, оно может быть представлено в виде упорядоченной пары значений переменных (x, y), где x и y являются корнями этих уравнений.
Решение системы уравнений с двумя переменными может быть найдено различными методами, такими как метод подстановки, метод сложения и вычитания, метод графического представления и метод определителей.
Определение и особенности
Особенностью системы уравнений с двумя переменными является то, что она представляет графическую модель, которая часто используется для решения задач геометрии и алгебры. Геометрически система уравнений с двумя переменными описывает пересечение двух кривых или линий на координатной плоскости.
Решение системы уравнений заключается в нахождении точек пересечения графиков обоих уравнений. В зависимости от вида системы, она может иметь одно решение, бесконечное количество решений или не иметь решений вовсе.
Решение системы уравнений с двумя переменными может быть найдено с помощью различных методов, включая графический метод, метод подстановки, метод сложения и вычитания, метод замены или метод Крамера.
Системы уравнений с двумя переменными широко применяются в различных областях науки и техники, включая физику, экономику, инженерию и компьютерные науки. Они позволяют моделировать и анализировать различные процессы и явления, а также находить оптимальные решения в различных ситуациях.
Решение системы уравнений с двумя переменными методом графического представления
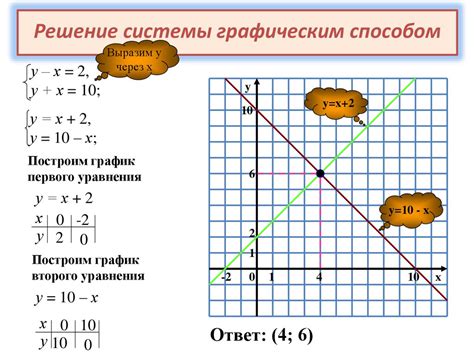
Для решения системы уравнений с двумя переменными методом графического представления необходимо:
- Записать уравнения системы в стандартной форме, то есть вида: ax + by = c.
- Построить графики уравнений на координатной плоскости.
- Найти точку пересечения графиков.
- Определить координаты найденной точки пересечения.
Если графики двух уравнений пересекаются в одной точке, то эта точка является решением системы уравнений. Если графики не пересекаются, то система уравнений не имеет решений. Если графики совпадают, то система имеет бесконечно много решений.
Пример:
Рассмотрим систему уравнений:
Уравнение 1: 2x + 3y = 8
Уравнение 2: 3x - 2y = 4
Построим графики уравнений на координатной плоскости:
Уравнение 1:
Уравнение 2:
Точка пересечения графиков соответствует решению системы уравнений. В данном случае, точка пересечения имеет координаты: (2, 1). Итак, решение системы уравнений: x = 2 и y = 1.
Таким образом, метод графического представления позволяет наглядно исследовать систему уравнений с двумя переменными и найти ее решение. Он основан на принципе пересечения графиков уравнений на координатной плоскости.
Применение систем уравнений с двумя переменными в реальной жизни

Системы уравнений с двумя переменными широко применяются в различных сферах реальной жизни. Они позволяют описывать и находить решения для разнообразных задач.
Одной из областей, где системы уравнений с двумя переменными используются, является экономика. В экономической сфере системы уравнений позволяют моделировать и анализировать зависимости между различными факторами. Например, с помощью систем уравнений можно рассчитать оптимальное соотношение выпуска продукции и затрат на производство.
Другим примером применения систем уравнений с двумя переменными является задача планирования маршрутов. При организации передвижения по городу или оптимизации транспортной логистики требуется найти оптимальный маршрут. Для этого можно использовать систему уравнений, где переменные - это координаты точек, а уравнения задаются на основе длин путей и времени путешествия.
Еще одним примером применения систем уравнений с двумя переменными является решение задач геометрии. Например, системы уравнений могут использоваться для нахождения точек пересечения прямых или окружностей. Это позволяет определить расположение и связи между геометрическими объектами.
Примеры систем уравнений с двумя переменными

Система уравнений с двумя переменными состоит из двух уравнений, в которых присутствуют две неизвестные величины. Решение такой системы состоит в нахождении значений переменных, которые удовлетворяют обоим уравнениям.
Рассмотрим несколько примеров систем уравнений с двумя переменными:
Пример 1:
Решим систему уравнений:
Уравнение 1: 2x + 3y = 8
Уравнение 2: 4x - y = 1
Для решения данной системы можно использовать метод подстановки или метод сложения/вычитания.
Один из способов решения данной системы:
Решим второе уравнение относительно одной из переменных:
y = 4x - 1
Подставим это выражение в первое уравнение:
2x + 3(4x - 1) = 8
Упростим уравнение:
2x + 12x - 3 = 8
14x = 11
x = 11/14
Теперь найдем значение переменной y, подставив найденное значение x в одно из уравнений:
y = 4 * (11/14) - 1
y = 44/14 - 1
y = 44/14 - 14/14
y = 30/14
Таким образом, решение системы уравнений равно x = 11/14 и y = 30/14.
Пример 2:
Решим систему уравнений:
Уравнение 1: x + y = 5
Уравнение 2: x - y = 3
Можно решить данную систему уравнений с помощью метода сложения/вычитания.
Сложим уравнения:
(x + y) + (x - y) = 5 + 3
2x = 8
x = 8/2
x = 4
Подставим найденное значение x в одно из уравнений:
4 - y = 3
y = 4 - 3
y = 1
Таким образом, решение системы уравнений равно x = 4 и y = 1.
Пример 3:
Решим систему уравнений:
Уравнение 1: 3x + 2y = 10
Уравнение 2: 6x + 4y = 20
Эта система уравнений имеет бесконечно много решений, так как уравнения пропорциональны друг другу. Любая точка на прямой 3x + 2y = 10 является решением этой системы.
Некоторые из решений:
x = 0, y = 5
x = 2, y = 2
x = 4, y = -1
и так далее...
Это лишь несколько примеров систем уравнений с двумя переменными. Хотя их решение может быть достаточно сложным, использование методов подстановки или сложения/вычитания помогает найти значения переменных, удовлетворяющие системе уравнений.





