Матрица - это таблица, состоящая из элементов, расположенных в отдельных ячейках. Одним из важных свойств матрицы является наличие диагоналей. Главная диагональ матрицы - это линия, которая проходит от верхнего левого угла до нижнего правого угла. Побочная диагональ, в свою очередь, проходит от верхнего правого угла до нижнего левого угла.
Главная и побочная диагонали имеют особое значение в матричных операциях. Главная диагональ является основной осью симметрии матрицы и, в некоторых случаях, содержит наиболее важные элементы. Например, в квадратной матрице на главной диагонали располагаются элементы, которые отражают симметричность исходных данных.
Побочная диагональ матрицы, хотя и менее распространена, также имеет свое значение. Эта диагональ может быть использована для определения влияния некоторых смежных элементов матрицы. В некоторых задачах, таких как нахождение среднего значения элементов матрицы, побочная диагональ может играть важную роль и влиять на итоговый результат.
Что такое главная диагональ матрицы?
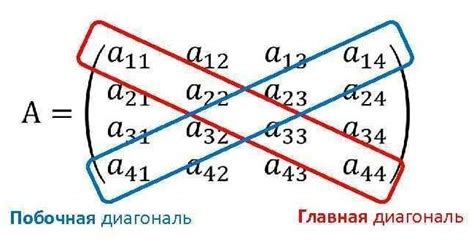
Каждый элемент главной диагонали представляет собой число, которое находится на пересечении строки и столбца с одинаковыми номерами. Например, в трехстрочной матрице следующие элементы являются частью главной диагонали: (1,1), (2,2) и (3,3).
Главная диагональ матрицы играет важную роль во многих аспектах математики и программирования. Она часто используется при выполнении операций над матрицами, таких как сложение, вычитание и умножение. Кроме того, она позволяет вычислить определитель матрицы и проверить ее симметричность.
Знание и понимание главной диагонали матрицы является необходимым для работы с матрицами и решения различных математических и программных задач.
Определение и особенности
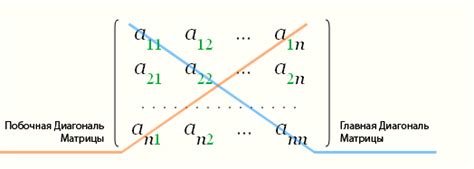
Главная диагональ матрицы - это линия, состоящая из элементов матрицы, находящихся на одном и том же уровне по вертикали и горизонтали. В других словах, это линия, начинающаяся в левом верхнем углу матрицы и заканчивающаяся в правом нижнем углу. Элементы, составляющие главную диагональ, имеют одинаковый индекс, т.е. их горизонтальный индекс равен вертикальному индексу.
Побочная диагональ матрицы, в свою очередь, это линия, соединяющая элементы матрицы, начиная с правого верхнего угла и заканчивая левым нижним углом. Элементы, составляющие побочную диагональ, имеют индексы, такие, что их сумма равна числу столбцов матрицы плюс один, применительно к индексам, начинающимся с 1.
Один из основных отличий между главной и побочной диагональю матрицы заключается в том, что главная диагональ идет по прямой линии, в то время как побочная диагональ идет в обратном направлении, образуя подобие обратной диагонали.
Главная и побочная диагональ матрицы являются важными инструментами для выполнения операций над матрицами, таких как сложение, вычитание, умножение и нахождение обратной матрицы. Знание и использование этих диагоналей помогает в решении математических задач и приложениях в различных областях, включая физику, экономику и компьютерную графику.
Побочная диагональ матрицы: отличия и применение
Побочная диагональ также имеет свои уникальные особенности и применения. Она может быть использована для вычисления следующих характеристик матрицы:
- Сумма элементов побочной диагонали;
- Произведение элементов побочной диагонали;
- Поиск минимального или максимального элемента побочной диагонали;
- Поиск количества отрицательных или положительных элементов побочной диагонали;
- Идентификация симметричности или антисимметричности побочной диагонали.
Кроме того, побочная диагональ матрицы имеет широкое применение во многих областях, таких как линейная алгебра, математическое моделирование, графическое программирование и т.д.
Знание о побочной диагонали матрицы и ее особенностях позволяет эффективно работать с данными и выполнять решения различных задач в математике и программировании.
Главная и побочная диагональ: сравнение и свойства

Главная диагональ матрицы - это множество элементов, расположенных на линии, идущей от верхнего левого угла матрицы до нижнего правого угла. Для квадратной матрицы главная диагональ состоит из элементов, у которых индексы строк и столбцов совпадают.
Побочная диагональ матрицы - это множество элементов, расположенных на линии, идущей от верхнего правого угла матрицы до нижнего левого угла. Для квадратной матрицы побочная диагональ состоит из элементов, у которых сумма индексов строк и столбцов равна размерности матрицы минус 1.
Главная и побочная диагональ имеют несколько важных свойств:
- Главная и побочная диагональ являются элементами матрицы и могут быть использованы в математических операциях над матрицами.
- Главная и побочная диагональ могут иметь различные значения и использоваться для разных целей.
- Главная и побочная диагональ могут быть использованы для вычисления определителя матрицы и других важных параметров матрицы.
- Главная и побочная диагонали могут быть использованы для определения симметричности и кососимметричности матрицы.
Понимание и использование главной и побочной диагонали полезно при решении различных задач в математике, физике, программировании и других науках. Они являются ключевыми элементами, окружающими матрицу, и отражают ее особенности и свойства.
Влияние главной диагонали на операции с матрицами

Одним из основных влияний главной диагонали является ее важная роль при умножении матриц. При умножении двух квадратных матриц элементы главной диагонали влияют на результат. В частности, если элементы главной диагонали в обоих матрицах равны 1, то элемент в результирующей матрице будет иметь значение, равное сумме произведений элементов соответствующих строк и столбцов.
Другим примером влияния главной диагонали является определение симметричности матрицы. Матрица считается симметричной, если элементы, расположенные относительно главной диагонали, равны. Это свойство позволяет использовать более эффективные алгоритмы для обработки симметричных матриц, что может значительно ускорить вычисления.
Главная диагональ также имеет значение для вычисления следа матрицы, который является суммой элементов главной диагонали. След матрицы является одним из основных показателей ее свойств и может использоваться для различных целей, например, в анализе систем линейных уравнений.
Таким образом, главная диагональ играет важную роль в операциях с матрицами. Ее значения и особенности не только влияют на результаты этих операций, но и оказывают влияние на эффективность вычислений и свойства матрицы в целом.
Преимущества и применение

1. Определение симметричности и обратимости матрицы: Главная диагональ матрицы сохраняется при операции транспонирования, а побочная диагональ меняет свой порядок. Это свойство можно использовать для проверки симметричности и обратимости матрицы.
2. Расчет следа матрицы: След матрицы - это сумма элементов на главной диагонали. Расчет следа может понадобиться для решения различных задач, таких как вычисление определителя матрицы или нахождение собственных значений.
3. Анализ разреженных матриц: Разреженные матрицы - это матрицы, в которых большинство элементов равно нулю. Главная и побочная диагонали часто содержат самые значимые элементы в таких матрицах, поэтому анализировать их содержимое может быть полезным, особенно при работе с большими объемами данных.
4. Решение систем линейных уравнений: Главная и побочная диагонали матрицы могут быть использованы для решения систем линейных уравнений методом итерации, например, методом Гаусса-Зейделя.
5. Обработка изображений и сигналов: Главная и побочная диагонали могут быть использованы для фильтрации изображений и сигналов, так как они содержат локальную информацию о структуре и связях элементов.
Все перечисленные применения свидетельствуют о важности и роли главной и побочной диагоналей матрицы в различных областях знаний, таких как математика, физика, информатика и др.
Роль побочной диагонали в алгоритмах и вычислениях
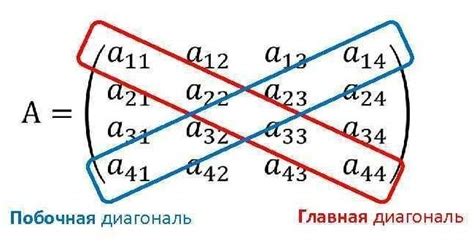
Побочная диагональ матрицы играет важную роль в различных алгоритмах и вычислениях. Ее значимость обусловлена тем, что значения элементов побочной диагонали образуют особую последовательность чисел, которая может быть использована для решения различных задач.
Одним из примеров использования побочной диагонали является определение суммы элементов данной диагонали. Для этого необходимо пройти по каждому элементу побочной диагонали и прибавить его значение к общей сумме. Такая операция может быть полезной, например, при вычислении следа матрицы или при анализе диагональных свойств матрицы.
Еще одним примером использования побочной диагонали является проверка симметричности матрицы относительно этой диагонали. Для этого необходимо сравнить значения элементов побочной диагонали с элементами, расположенными на противоположной стороне от нее. Если все значения совпадают, то матрица симметрична относительно побочной диагонали.
Побочная диагональ также может быть полезна при поиске максимального или минимального элемента матрицы. Для этого необходимо пройти по каждому элементу побочной диагонали и сравнить его значение с текущим максимальным или минимальным. Это может быть особенно полезно, если в матрице существует закономерность, связанная с побочной диагональю, например, если элементы побочной диагонали представляют собой упорядоченную последовательность чисел.
Таким образом, побочная диагональ играет важную роль в алгоритмах и вычислениях, облегчая решение различных задач и анализ матрицы. Знание особенностей и возможностей побочной диагонали поможет более эффективно использовать ее в своей работе.
Примеры использования
Главная и побочная диагональ матрицы широко применяются в различных областях, включая математику, физику, программирование и науку о данных. Ниже приведены некоторые примеры использования этих диагоналей:
1. Математика:
Главная и побочная диагонали матриц используются для решения квадратных систем линейных уравнений, определения собственных значений и векторов матрицы, а также для вычисления определителя матрицы.
2. Физика:
В физике главная диагональ матрицы может представлять значения физических величин, таких как время, масса или энергия, в определенный промежуток времени или координат. Побочная диагональ может использоваться для представления дополнительных свойств или параметров системы.
3. Программирование:
Главная и побочная диагональ матрицы могут быть использованы в программировании для обработки данных, например, в алгоритмах сортировки, обходе массивов или поиске в матрице. Они также используются в машинном обучении для работы с данными и вычисления различных статистических метрик.
4. Наука о данных:
В науке о данных главная и побочная диагональ матрицы используются для анализа и визуализации данных. Они могут представлять значения переменных или признаков в наборе данных, а также использоваться для проверки корреляции или зависимости между переменными.
Использование главной и побочной диагонали матрицы зависит от конкретной задачи или контекста, в котором они применяются. Однако, они являются важными инструментами для работы с данными и анализа информации в различных областях знания.
Значение главной и побочной диагонали при решении задач линейной алгебры

Главная и побочная диагонали матрицы играют важную роль при решении задач линейной алгебры. Значения элементов на этих диагоналях содержат важную информацию о матрице и позволяют нам получить ценные результаты и свойства.
Главная диагональ матрицы - это набор элементов, расположенных на линии, которая идет от левого верхнего угла матрицы до правого нижнего угла. Значения на главной диагонали обозначаются как aii, где i - номер строки и столбца, на которых находится элемент. Главная диагональ является важной характеристикой матрицы и используется во многих операциях, таких как вычисление определителя и нахождение собственных значений.
Побочная диагональ матрицы - это набор элементов, расположенных на линии, которая идет от правого верхнего угла матрицы до левого нижнего угла. Значения на побочной диагонали обозначаются как aij, где i - номер строки, а j - номер столбца, на которых находится элемент. Побочная диагональ также имеет важное значение в линейной алгебре и используется, например, при транспонировании матрицы и вычислении следа.
Значения на главной и побочной диагоналях матрицы могут быть как числами, так и переменными. Это позволяет нам решать задачи линейной алгебры с использованием формул и алгоритмов, основанных на этих диагоналях. Например, сумма элементов на главной диагонали матрицы может быть использована для определения следа матрицы, который имеет важное значение для вычислений векторов и матриц.
Важно помнить, что главная и побочная диагонали матрицы являются взаимоисключающими и не пересекаются. Каждый элемент матрицы находится только на одной из этих диагоналей. Изучение значений на этих диагоналях позволяет нам лучше понять и работать с матрицами в линейной алгебре.



