Десятичный эквивалент числа в информатике является одним из важных понятий, которое позволяет нам переводить числа из одной системы счисления в другую. Использование различных систем счисления широко распространено в информатике и программировании, и понимание десятичного эквивалента помогает нам в работе с числами.
Для того чтобы понять, что такое десятичный эквивалент числа, необходимо разобраться с понятием системы счисления. Система счисления - это способ записи чисел с использованием определенного набора цифр и правил преобразования из одной цифры в другую. В десятичной системе счисления мы используем 10 цифр: от 0 до 9.
Для перевода числа из другой системы счисления в десятичную систему необходимо умножить каждую цифру числа на соответствующую ей степень основания системы счисления и сложить полученные произведения. Например, для числа в двоичной системе счисления 1011, его десятичный эквивалент будет 11.
Понятие десятичного эквивалента числа в информатике позволяет нам более удобно работать с числами других систем счисления, представляя их в десятичной форме. Это особенно полезно при выполнении арифметических операций над числами разных систем счисления или при сравнении чисел в разных системах.
Определение и сущность десятичного эквивалента числа
Десятичная система счисления является наиболее распространенной и используется повсеместно в повседневной жизни, а также в информатике. В этой системе каждая цифра в числе имеет вес, зависящий от ее позиции в записи числа.
Сущность десятичного эквивалента числа заключается в том, что оно представляет одно и то же значение, что и исходное число, но в десятичной системе счисления. То есть десятичный эквивалент числа – это результат преобразования числа из одной системы счисления в десятичную.
Преобразование числа в десятичный эквивалент позволяет легче выполнять математические операции с числами и проводить сравнение чисел. Более того, десятичная система счисления является интуитивно понятной и широко используется в коммерческих расчетах.
Десятичный эквивалент числа может иметь большое значение в информатике, особенно при работе с большими числами или при необходимости точного представления числа.
Как вычислить десятичный эквивалент

Для вычисления десятичного эквивалента числа в информатике нужно учитывать используемую систему счисления и правила преобразования.
Если число представлено в двоичной системе счисления, то для вычисления его десятичного эквивалента необходимо умножить каждую цифру числа на соответствующую степень числа 2 и сложить полученные произведения. Например, число 1011 в двоичной системе счисления имеет десятичный эквивалент 11, так как 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 8 + 0 + 2 + 1 = 11.
Если число представлено в восьмеричной системе счисления, то для вычисления его десятичного эквивалента нужно умножить каждую цифру числа на соответствующую степень числа 8 и сложить полученные произведения. Например, число 37 в восьмеричной системе счисления имеет десятичный эквивалент 31, так как 3 * 8^1 + 7 * 8^0 = 24 + 7 = 31.
Если число представлено в шестнадцатеричной системе счисления, то для вычисления его десятичного эквивалента нужно умножить каждую цифру числа на соответствующую степень числа 16 и сложить полученные произведения. При этом, для цифр A, B, C, D, E, F используются соответствующие числовые значения: A – 10, B – 11, C – 12, D – 13, E – 14 и F – 15. Например, число 2D в шестнадцатеричной системе счисления имеет десятичный эквивалент 45, так как 2 * 16^1 + 13 * 16^0 = 32 + 13 = 45.
Зная систему счисления и правила преобразования, можно вычислить десятичный эквивалент числа в информатике. Этот процесс является основой для работы с числами в компьютерных программировании и информационных системах.
Важность десятичного эквивалента в информатике

Одной из основных причин важности десятичного эквивалента в информатике является его привычность и понятность для людей. Многие пользователи компьютеров и программ не имеют специальных знаний в области информатики, и для них десятичная система счисления является наиболее интуитивно понятной. Поэтому использование десятичного эквивалента числа позволяет легче воспринимать и анализировать информацию.
Кроме того, десятичный эквивалент часто используется при взаимодействии компьютерных систем с внешним миром. Во многих случаях данные, которые поступают в компьютер или передаются из него, представлены в десятичной форме. Например, при передаче данных через сеть, адреса IP и порты также представлены в виде десятичных чисел.
Десятичный эквивалент также играет важную роль при работе с дробными числами. В информатике десятичная система счисления позволяет точно представлять и оперировать десятичными дробями. Это особенно важно для финансовых и бухгалтерских приложений, где точность вычислений имеет решающее значение.
Применение десятичного эквивалента в программировании

Одним из основных применений десятичного эквивалента является работа с числами в 10-ичной системе счисления. В программировании часто используется двоичная система счисления, но для удобства ввода и отображения данных, а также для выполнения арифметических операций, часто требуется преобразование чисел из двоичной системы в десятичную.
Для преобразования числа из двоичной системы в десятичную, можно использовать алгоритм пошагового умножения. В этом случае каждая цифра двоичного числа будет умножаться на соответствующую степень числа 2 и складываться. Например, для числа 1101 результатом будет 1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 13.
Другим применением десятичного эквивалента является конвертация чисел между разными системами счисления. Например, при разработке программ, связанных с работой с компьютерными сетями, может потребоваться работать с IP-адресами, которые представляют собой четырехразрядные числа в 10-ичной системе счисления. В таких случаях для работы с IP-адресами в программе необходимо преобразовывать числа из двоичной системы в десятичную и обратно.
Также десятичный эквивалент используется для работы с числами в шестнадцатеричной системе счисления. В этом случае каждая цифра шестнадцатеричного числа будет умножаться на соответствующую степень числа 16 и складываться. Такое представление чисел удобно для работы с цветами, так как каждая компонента цвета (красная, зеленая и синяя) обычно представляется двузначным шестнадцатеричным числом.
| Система счисления | Пример | Десятичный эквивалент |
|---|---|---|
| Двоичная | 1010 | 10 |
| Шестнадцатеричная | FF | 255 |
Таким образом, десятичный эквивалент числа является незаменимым инструментом в программировании и позволяет работать с числами разных систем счисления, упрощая выполнение различных операций и конвертацию чисел между ними.
Особенности кодирования десятичного эквивалента числа
Кодирование десятичного эквивалента числа в информатике имеет несколько особенностей, которые важно учитывать при работе с числовыми данными.
- Точность представления чисел. При кодировании десятичных чисел в компьютере возможна потеря точности из-за ограничений на количество бит, выделенных для хранения числа. Это означает, что некоторые десятичные числа могут быть представлены с небольшой погрешностью.
- Округление чисел. Десятичные числа часто округляются при кодировании для уменьшения размера хранения и облегчения вычислений. Но округление может привести к потере точности, особенно при последовательных операциях над числами.
- Перевод между различными кодировками. При обмене десятичными данными между различными системами или программами может потребоваться перевод чисел из одной кодировки в другую. Это может привести к дополнительной потере точности или ошибкам округления.
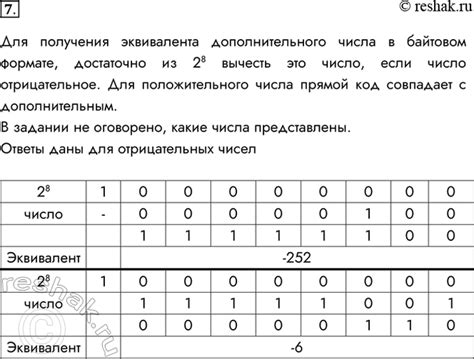
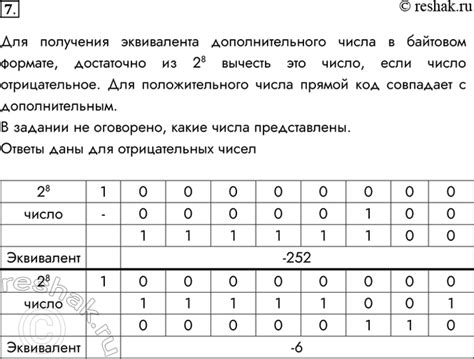
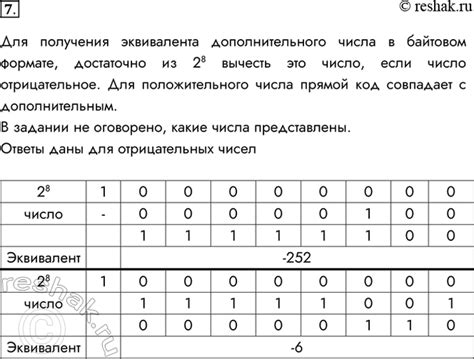
- Представление отрицательных чисел. Для представления отрицательных десятичных чисел используются специальные кодировки, такие как дополнительный код или знаковое представление. При работе с отрицательными числами необходимо учитывать особенности выбранной кодировки.
Учитывая эти особенности, программисты и инженеры должны быть внимательными при работе с десятичными числами в информатике. Необходимо правильно выбирать типы данных, кодировки и алгоритмы для обработки числовых данных, чтобы минимизировать потерю точности и сохранить корректность результатов вычислений.
Проблемы и ограничения десятичного эквивалента числа в информатике
В информатике существует некоторые проблемы и ограничения, связанные с представлением чисел в десятичной системе счисления. Вот некоторые из них:
Округление и потеря точности: При работе с десятичным эквивалентом числа могут возникать проблемы с округлением и потерей точности. В частности, некоторые десятичные дроби не могут быть точно представлены в бинарной системе счисления, что может привести к ошибкам в результате вычислений.
Ограниченная точность: В системах с плавающей точкой числа представляются с ограниченной точностью. Это означает, что некоторые числа могут быть округлены или обрезаны, что может привести к неточным результатам вычислений.
Проблемы с переводом: При переводе чисел из одной системы счисления в другую могут возникать проблемы с точностью и целостностью данных. Например, при переводе десятичного числа в двоичное представление могут возникать ошибки, связанные с округлением и потерей точности.
Ограничения представления чисел: В некоторых системах счисления существуют ограничения на диапазон представления чисел. Например, система Int в языке программирования Java может представлять только целые числа в диапазоне от -231 до 231-1, что ограничивает возможности работы с большими числами.
Необходимость учета этих проблем и ограничений является важной задачей при работе с десятичным эквивалентом числа в информатике. Разработчики и программисты должны быть внимательными к возможным проблемам и применять соответствующие методы и алгоритмы для минимизации ошибок и потерь точности.
Альтернативы и расширения десятичного эквивалента числа

Помимо десятичного эквивалента числа, существуют и другие системы счисления, которые могут быть использованы в информатике. Некоторые из них:
Бинарная система счисления: В бинарной системе счисления используются только две цифры - 0 и 1. Она широко используется в компьютерах и переводится в десятичную систему путем умножения каждой цифры на соответствующую степень двойки и сложения полученных результатов.
Восьмеричная система счисления: В восьмеричной системе счисления используется восемь цифр - от 0 до 7. Она часто используется для представления машинных кодов.
Шестнадцатеричная система счисления: Шестнадцатеричная система счисления использует шестнадцать цифр - от 0 до 9 и от A до F. Она позволяет удобно представлять большие числа и широко используется в программировании и компьютерных системах.
Каждая из этих систем имеет свои преимущества и недостатки и может быть использована в зависимости от конкретной задачи. Важно уметь преобразовывать числа из одной системы счисления в другую, чтобы успешно работать в информатике.



