Делимое - это число, которое делится на другое число без остатка. В математике 3 класса мы изучаем основы деления и понятие делимое является одним из ключевых. Понимание этого понятия поможет правильно выполнять деление и решать задачи в школьном курсе математики.
Чтобы понять, что такое делимое, нужно знать, что деление является одной из основных арифметических операций. Оно позволяет разделить одно число на другое и найти результат такого деления. Для выполнения деления необходимо знать два числа: делимое и делитель. Делимое - это число, которое мы делим, а делитель - это число, на которое мы делим. В результате деления получается частное, которое может быть как целым, так и дробным числом.
Например, если у нас есть задача "Разделить 10 конфет поровну между 2 друзьями", то число 10 является делимым, так как мы его делим на 2. Если мы разделим 10 конфет поровну между двумя друзьями, то каждый получит по 5 конфет. В этом примере делимое - число 10, а делитель - число 2. Частное от деления будет равно 5.
Математика в 3 классе

Одной из важных тем, которую изучают в 3 классе, является понятие "делимое". В математике число, которое делится на другое число без остатка, называется делимым. Например, число 12 является делимым на 3, так как его можно разделить на 3 равные части без остатка.
Для понимания принципов деления и определения делимых чисел, в 3 классе используются различные методики и игры. Это помогает детям запомнить правила деления и развить логическое мышление.
Знание понятия "делимое" является базовым для дальнейшего изучения математики. С помощью этого понятия дети смогут освоить более сложные темы, такие как дроби и проценты, которые будут изучаться в старших классах.
Понимание понятия "делимое" поможет детям решать различные задачи и применять математические навыки в реальной жизни. Например, при дележе конфет или игрушек наравне между детьми, знание деления и делимых чисел поможет им справиться с задачей и разделить ресурсы равномерно.
Таким образом, изучение понятия "делимое" в 3 классе является важным шагом на пути к развитию математических навыков и логического мышления у детей. Это знание поможет им в дальнейшем учебном пути и в решении повседневных задач.
Определение понятия

В математике понятие "делимое" относится к числам и отражает их способность быть разделенными на равные части без остатка. Число, которое может быть разделено на другое число без остатка, называется делимым, а число, на которое можно разделить без остатка, называется делителем.
В третьем классе учащимся объясняют, что в предметной области математики мы можем делить только некоторые числа без остатка. Например, число 12 является делимым на 2, потому что оно может быть разделено на 2 равные части: 12 ÷ 2 = 6. Также 12 является делимым на 3 (12 ÷ 3 = 4) и на 4 (12 ÷ 4 = 3).
Понятие делимости является основой для понимания других математических операций, таких как умножение и деление. В процессе изучения делимых чисел и их делителей в третьем классе дети учатся находить результаты деления, определять делимость чисел на заданный делитель и решать задачи на деление.
Что такое делимое?

В математике понятие "делимое" используется для описания числа, которое может быть разделено на другое число без остатка. Процесс разделения одного числа на другое называется делением.
Чтобы понять, что число является делимым, необходимо убедиться, что оно делится на другое число без остатка. Например, число 12 является делимым на 3, так как 12 делится на 3 без остатка: 12 ÷ 3 = 4. Но число 13 не является делимым на 3, так как при делении его на 3 получается остаток: 13 ÷ 3 = 4 и остаток 1.
Чтобы сказать, что одно число делится на другое число, мы можем использовать специальные математические символы. Символом деления является горизонтальная черта с двумя точками над ней. Например, 12 делится на 3 записывается как 12 : 3 = 4.
Знание понятия "делимое" позволяет решать различные задачи на деление и проводить математические операции более точно. Кроме того, оно является основой для изучения других понятий, связанных с делением, таких как частное и остаток.
Правила делимости

В математике существуют различные правила делимости. Рассмотрим некоторые из них:
Правило делимости на 2: Число делится на 2 без остатка, если его последняя цифра является четной (0, 2, 4, 6 или 8).
Правило делимости на 3: Число делится на 3 без остатка, если сумма его цифр также делится на 3.
Правило делимости на 5: Число делится на 5 без остатка, если его последняя цифра является 0 или 5.
Правило делимости на 10: Число делится на 10 без остатка, если его последняя цифра равна 0.
Запомнить правила делимости поможет упражнение и практика. При решении числовых задач важно учитывать эти правила, чтобы деление проходило быстрее и точнее.
Делимость на 2

Когда число делится на 2 без остатка, оно называется четным числом. В противном случае, когда число не делится на 2 без остатка, оно называется нечетным числом.
Например, число 4 является четным, так как оно делится на 2 без остатка. А число 5 является нечетным, так как при делении на 2 остаток будет равен 1.
Делимость на 2 имеет свои особенности. Четное число, например, всегда можно разделить на 2 и получить другое четное число. Например, 8:2=4.
Также, если число оканчивается на 0, 2, 4, 6 или 8, то оно обязательно является четным. Например, числа 20, 52, 76 являются четными числами.
Делимость на 2 активно используется в различных областях математики, физики и программирования. Она помогает проводить различные вычисления и анализ числовых данных.
Делимость на 3

Для того чтобы понять, делится ли число на 3, нужно посчитать сумму его цифр. Если эта сумма делится на 3, то исходное число также делится на 3.
Например, рассмотрим число 123. Сумма его цифр равна 1 + 2 + 3 = 6. Так как 6 делится на 3 без остатка, то число 123 также делится на 3.
Другой пример - число 217. Сумма его цифр равна 2 + 1 + 7 = 10. Так как 10 не делится на 3 без остатка, то число 217 не делится на 3.
Делимость на 3 является одним из простых правил, которые можно использовать при делении чисел. Зная это свойство, можно легко определить, делится ли число на 3 или нет.
Помните, что данное правило работает только для деления на 3 и не применимо к другим числам.
Делимость на 4

Правило делимости на 4 состоит в том, что число является делимым на 4, если две последние цифры числа образуют число, которое само по себе делится на 4. Например, число 1248 является делимым на 4, потому что 48 делится на 4 без остатка. А число 5372 не является делимым на 4, потому что 72 не делится на 4 без остатка.
Чтобы определить, является ли число делимым на 4, достаточно проверить последние две цифры числа. Если они образуют число, которое делится на 4, то исходное число также является делимым на 4. В противном случае, число не является делимым на 4.
Примеры чисел, которые делятся на 4 без остатка: 12, 696, 2480, 7524.
Примеры чисел, которые не делятся на 4 без остатка: 5372, 191, 3701, 808.
| Число | Делимость на 4 |
|---|---|
| 12 | Да |
| 686 | Нет |
| 2480 | Да |
| 3701 | Нет |
Делимость на 5

В математике есть правило, по которому можно определить, делится ли число на 5. Если последняя цифра числа является 0 или 5, то число делится на 5.
Примеры:
- 10 делится на 5, так как последняя цифра 0.
- 25 делится на 5, так как последняя цифра 5.
- 7 не делится на 5, так как последняя цифра не 0 или 5.
Чтобы проверить, делится ли число на 5, нужно просто посмотреть на его последнюю цифру.
Делимость на 5 важна в математике и может использоваться, например, при решении задач с делением и умножением.
Как проверить делимость числа

- Выберите число, которое вы хотите проверить на делимость.
- Выберите число, на которое вы хотите проверить деление.
- Проверьте, делится ли выбранное число без остатка на выбранное число для деления.
- Если выбранное число делится без остатка, то это означает, что оно является делителем выбранного числа. Если выбранное число не делится без остатка, то это означает, что оно не является делителем выбранного числа.
Например, чтобы проверить, делится ли число 10 на число 2, нужно поделить 10 на 2. Если результат деления равен 5, то число 2 является делителем числа 10. Если результат деления не равен 5, то число 2 не является делителем числа 10.
Таким образом, для проверки делимости числа на другое число, необходимо выполнить деление и проверить наличие остатка. Если остаток от деления равен нулю, то число является делителем, в противном случае - не является.
Алгоритм проверки делимости
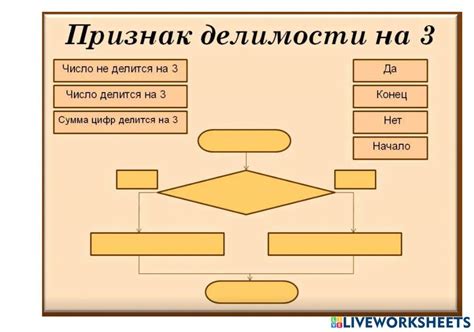
Алгоритм проверки делимости позволяет определить, делится ли одно число на другое без остатка. Для этого необходимо следовать следующим шагам:
- Выбрать два числа: делимое и делитель.
- Проверить, что делитель не равен нулю.
- Поделить делимое на делитель.
- Если остаток от деления равен нулю, значит, число делится без остатка и является делимым. Если остаток не равен нулю, то число не делится без остатка и не является делимым.
Например, чтобы проверить, делится ли число 15 на 3, нужно:
Делимое = 15
Делитель = 3
15 ÷ 3 = 5 остаток 0
Так как остаток равен нулю, число 15 делится на 3 без остатка и является делимым.
Этот алгоритм поможет третьеклассникам проверять делимость чисел и решать простые задачи по математике.



