Декартовые координаты являются незаменимым инструментом в математике и физике, позволяющим определить положение точки на плоскости или в пространстве. Однако они также могут быть применены и на числовой окружности, что расширяет их область применения и придает им новые свойства.
Числовая окружность – это математическая конструкция, представляющая собой окружность, на которой расположены все числа из интервала [-1, 1]. Таким образом, каждому числу соответствует определенная точка на окружности.
Декартовые координаты на числовой окружности определяются с помощью двух параметров: угла и радиуса. Угол измеряется от оси абсцисс против часовой стрелки, а радиус представляет собой расстояние от начала координат до точки на окружности. Таким образом, каждой точке на окружности соответствует определенная пара координат (угол, радиус).
Применение декартовых координат на числовой окружности позволяет удобно и наглядно решать задачи, связанные с синусами, косинусами и другими тригонометрическими функциями. Кроме того, они являются основой для работы с комплексными числами, которые тесно связаны с числовой окружностью.
Что такое декартовые координаты на числовой окружности?
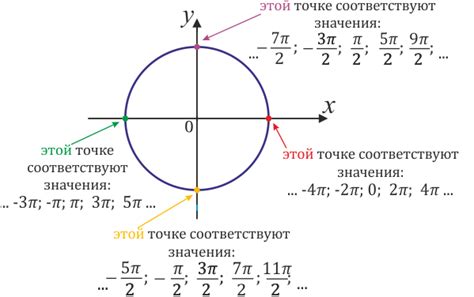
Числовая окружность представляет собой особый вид координатной плоскости, где ось абсцисс (горизонтальная ось) и ось ординат (вертикальная ось) замкнуты в круг, причем начало координат совпадает с точкой пересечения этих двух осей.
Декартовыми координатами на числовой окружности можно задать любую точку на окружности. Например, точка с координатами (1, 0) будет находиться на правой стороне круга, точка с координатами (0, 1) - на верхней стороне, точка с координатами (-1, 0) - на левой стороне, а точка с координатами (0, -1) - на нижней стороне окружности.
| x | y | Положение точки на окружности |
|---|---|---|
| 1 | 0 | правая сторона |
| 0 | 1 | верхняя сторона |
| -1 | 0 | левая сторона |
| 0 | -1 | нижняя сторона |
Декартовыми координатами на числовой окружности также могут быть значения, превышающие единичную длину. Например, точка с координатами (2, 0) будет находиться на расстоянии двух единиц от начала координат. Негативные значения координат указывают на противоположную сторону от начала координат.
Декартовые координаты на числовой окружности широко используются в различных областях, таких как математика, физика, компьютерная графика и др. Они позволяют точно определить положение объектов и проводить различные вычисления, связанные с их перемещением и взаимодействием на окружности.
Примеры использования декартовых координат на числовой окружности
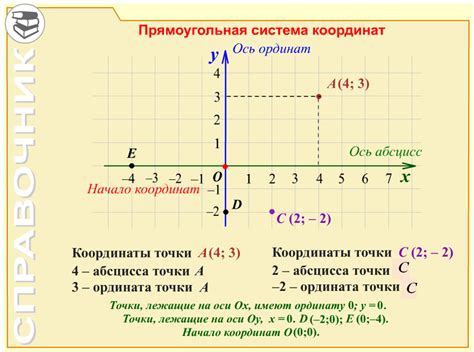
Декартовы координаты на числовой окружности используются во множестве областей, включая геометрию, физику и информатику. Ниже приведены несколько примеров, демонстрирующих применение этой концепции.
- Геометрия: Декартовы координаты на числовой окружности позволяют определить положение точки на окружности. Например, чтобы найти координаты точки, лежащей на окружности с радиусом 1 и центром в начале координат, можно использовать тривиальное соотношение (cos(θ), sin(θ)), где θ - заданный угол.
- Физика: Декартовы координаты на числовой окружности применяются для описания движения тела в плоскости. Например, при моделировании движения планеты вокруг солнца, можно использовать декартовы координаты для определения положения планеты относительно солнца в каждый момент времени.
- Информатика: Декартовы координаты на числовой окружности используются в алгоритмах компьютерной графики для отображения и манипулирования графическими объектами. Например, при рисовании эллипса с помощью алгоритма Брезенхема можно использовать декартовы координаты на окружности для определения положения пикселей на экране.
Таким образом, декартовые координаты на числовой окружности имеют широкий спектр применения в различных областях науки и техники, позволяя удобно описывать и анализировать разнообразные явления и процессы.



