Математика - это одна из самых важных дисциплин, которая развивает логическое мышление и способности к анализу. Числовые выражения играют большую роль в изучении математики, особенно в начальной школе. Именно через числовые выражения дети учатся решать простые и сложные задачи, применять различные математические операции.
Числовое выражение - это математическое выражение, состоящее из чисел, знаков операций (сложение, вычитание, умножение, деление) и скобок. Дети изучают числовые выражения с 4-5 класса, начиная с основных операций. Они учатся считать, выполнять простые действия с числами, записывать выражения и решать простейшие уравнения.
Примеры числовых выражений для 5 класса:
1. Пример с операцией сложения:
3 + 5
В данном примере сложили два числа: 3 и 5. Получилось число 8.
2. Пример с операцией вычитания:
10 - 4
В данном примере вычли из числа 10 число 4. Получилось число 6.
3. Пример с операцией умножения:
7 * 2
В данном примере умножили число 7 на число 2. Получилось число 14.
4. Пример с операцией деления:
12 / 3
В данном примере числу 12 разделили на число 3. Получилось число 4.
Числовые выражения - это основа для понимания математики и образ мышления в будущем. Они помогают ученикам решать различные задачи и уметь анализировать числовую информацию. Поэтому важно освоить основы работы с числовыми выражениями и тренироваться в их решении.
Числовое выражение: что это и зачем нужно учить в 5 классе?

Зачем это нужно учить? Ведь можно просто сложить или вычесть числа без всей этой сложной нотации. Однако, знание числовых выражений позволяет нам:
- Упростить сложные вычисления. Если у нас есть длинная арифметическая задача, то записывая ее в виде числового выражения, мы сможем легко и быстро выполнить все вычисления поочередно.
- Лучше понять структуру арифметической операции. Когда мы записываем выражение, мы видим, какие числа участвуют в операции, какая операция выполняется с ними и в каком порядке. Это помогает нам осознать смысл арифметических действий.
- Решать сложные задачи с помощью выражений. В жизни мы часто сталкиваемся с задачами, которые требуют применения нескольких арифметических операций. Знание и понимание числовых выражений позволяет нам разбивать сложные задачи на элементарные шаги и решать их поочередно.
В 5 классе дети начинают знакомиться с основами числовых выражений. Они учатся записывать выражения с использованием арифметических операций: сложения, вычитания, умножения и деления. Также они учатся использовать скобки для задания порядка выполнения операций.
Самое главное в изучении числовых выражений - это понимание их логики и правил. Дети учатся читать и анализировать выражения, определять значение переменных и выполнять указанные операции по заданному порядку.
Изучение числовых выражений в 5 классе является важной основой для дальнейшего изучения математики. Понимая, как работают числовые выражения, дети смогут успешно решать различные задачи и развивать свои аналитические и логические навыки.
Основные понятия и определения

В математике числовое выражение представляет собой комбинацию чисел, операций и обозначений. Оно может быть записано в виде алгебраического выражения или уравнения.
Операции - это действия, выполняемые над числами, такие как сложение, вычитание, умножение и деление. Обозначения используются для представления операций и переменных.
Термины числового выражения:
- Числа: основные величины, используемые в выражении. Могут быть целыми числами, дробями или десятичными дробями.
- Переменные: символы, представляющие неизвестные значения или значения, которые могут изменяться.
- Операторы: специальные символы или знаки, используемые для выполнения математических операций, таких как сложение (+), вычитание (-), умножение (*) и деление (/).
- Скобки: символы, используемые для указания порядка выполнения операций или для группировки частей выражения.
Например, в выражении "2 + 3 * (4 - 1)" числа 2 и 3 являются операндами операции сложения, а числа 4 и 1 - операндами операции вычитания. Скобки указывают, что вычитание должно быть выполнено перед умножением.
Порядок действий в числовых выражениях: как считать?

При решении числового выражения следует придерживаться следующих шагов:
- Скобки: Выполняйте действия внутри скобок в первую очередь. Если в выражении присутствуют несколько пар скобок, считайте сначала внутренние, затем внешние.
- Умножение и деление: После раскрытия всех скобок выполните операции умножения и деления слева направо. Умножение и деление имеют одинаковый приоритет и выполняются раньше сложения и вычитания.
- Сложение и вычитание: После завершения операций умножения и деления выполняйте операции сложения и вычитания слева направо.
Приведем пример, чтобы лучше понять этот порядок:
Вычислим значение выражения 3 + 2 * 4:
- Сначала выполним умножение: 2 * 4 = 8.
- Затем сложение: 3 + 8 = 11.
Таким образом, значение выражения 3 + 2 * 4 равно 11.
Соблюдение порядка действий в числовых выражениях позволяет получать правильные результаты и избегать ошибок. Помните об этом при решении математических задач и вычислении числовых выражений!
Операции в числовых выражениях: сложение, вычитание, умножение, деление
Сложение двух или более чисел производится путем суммирования значений этих чисел. Например, числовое выражение "5 + 3" означает сложение числа 5 и числа 3, что дает результат 8.
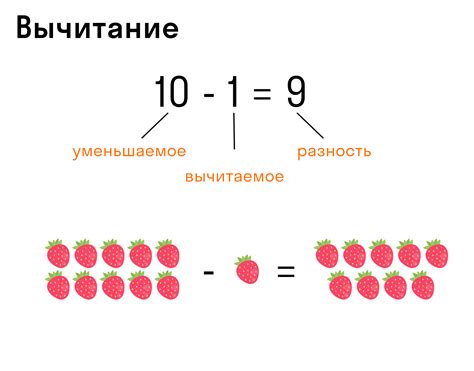
Вычитание является обратной операцией сложения и позволяет находить разность двух чисел. Например, числовое выражение "7 - 4" означает вычитание числа 4 из числа 7, что дает результат 3.
Умножение позволяет находить произведение двух или более чисел. Например, числовое выражение "2 * 6" означает умножение числа 2 на число 6, что дает результат 12.
Деление позволяет находить отношение одного числа к другому. Например, числовое выражение "10 / 2" означает деление числа 10 на число 2, что дает результат 5.
Операции в числовых выражениях могут быть комбинированы и выполняться в определенном порядке. Для изменения порядка выполнения операций можно использовать скобки. Например, числовое выражение "3 * (4 + 2)" означает, что сначала нужно выполнить сложение в скобках, а затем умножить результат на 3.
Правила знаков в числовых выражениях: как определить результат?

Когда мы работаем с числовыми выражениями в математике, очень важно знать правила, определяющие знак результата. Эти правила помогут нам правильно выполнять операции и получать точные ответы.
1. Если в выражении только положительные числа, например, 5 + 3, то результат также будет положительным: 5 + 3 = 8.
2. Если в выражении только отрицательные числа, например, -4 - 2, то результат будет отрицательным: -4 - 2 = -6.
3. Если в выражении есть как положительные, так и отрицательные числа, то необходимо обратить внимание на их знаки и выполнять операции в соответствии с правилами:
- Если знаки чисел одинаковые (оба положительные или оба отрицательные), то нужно сложить или вычесть числа и сохранить знак результата. Например, 6 + (-2) = 4.
- Если знаки чисел разные (одно положительное, другое отрицательное), то нужно вычесть из большего числа меньшее и сохранить знак числа с большим модулем. Например, 5 - (-3) = 8.
4. Если в выражении есть скобки, то для определения знака результата следует сначала выполнить операцию внутри скобок, а затем применить описанные выше правила.
Знание правил знаков в числовых выражениях поможет нам с уверенностью выполнять различные математические задачи и получать верные результаты.
Примеры числовых выражений в 5 классе: решение задач
В пятом классе ученики изучают основы математики, в том числе и числовые выражения. Числовые выражения представляют собой комбинацию чисел, знаков операций и скобок. Они используются для записи математических операций и решения различных задач.
Рассмотрим несколько примеров числовых выражений и их решение:
| Пример выражения | Решение |
|---|---|
| 2 + 3 | Результат: 5 |
| 4 * 5 | Результат: 20 |
| (7 - 2) * 3 | Результат: 15 |
| 20 / (4 + 1) | Результат: 4 |
В первом примере происходит сложение чисел 2 и 3, что дает результат 5. Во втором примере происходит умножение чисел 4 и 5, результатом которого является число 20. Третий пример демонстрирует использование скобок, в которых выполняются операции сложения и вычитания. В результате получаем число 15. В последнем примере сложение чисел 4 и 1 выполняется в скобках, а затем число 20 делится на сумму, результатом чего является число 4.
Решая задачи, связанные с числовыми выражениями, ученики могут использовать знаки операций, скобки и арифметические правила для получения правильных ответов. Решение задач на числовые выражения помогает развивать логическое мышление и навыки работы с числами.
Упрощение числовых выражений: откуда взялись скобки?

Скобки в числовых выражениях помогают определить порядок действий и уточнить, какие операции нужно выполнить в первую очередь. Например, выражение (2 + 3) * 4 говорит нам, что сначала нужно сложить 2 и 3, а затем умножить результат на 4. Если бы скобок не было, пришлось бы умножить 2 на 3, а затем сложить с 4, что дало бы нам неверный ответ.
С помощью скобок мы также можем группировать части выражений и обозначать их отдельно, чтобы легче проводить расчеты. Например, выражение (10 - 5) * 2 говорит нам, что нужно сначала вычесть 5 из 10, а затем умножить результат на 2. Без скобок мы не смогли бы ясно указать, что нужно вычесть 5 из 10 первым действием.
Использование скобок в числовых выражениях является важным и необходимым элементом, позволяющим правильно и однозначно определить порядок выполнения операций. При решении задач не забывайте об этом инструменте и используйте его, если необходимо уточнить порядок действий и упростить выражение.
Числовые выражения и алгебраические выражения: в чем разница?

Числовые выражения - это выражения, в которых используются только числа, операции сложения, вычитания, умножения и деления, а также скобки для изменения порядка действий. Примерами числовых выражений могут служить:
- 5 + 3
- 9 * 2
- 10 - 4 + 2
В числовых выражениях значения всех чисел уже известны, и их можно вычислить, чтобы получить определенный результат.
Алгебраические выражения - это выражения, в которых используются не только числа, но и переменные, которые могут принимать различные значения. Примерами алгебраических выражений могут служить:
- 2x + 3
- 4y - 5x
- a^2 + b^2
В алгебраических выражениях мы работаем с переменными, и значения этих переменных могут быть любыми. Мы можем подставить конкретные значения переменных и вычислить результат.
Таким образом, основным отличием между числовыми и алгебраическими выражениями является наличие переменных в последних. Этот факт позволяет нам решать более сложные задачи и работать с неизвестными значениями.



