Частное и произведение – две фундаментальные операции в математике, которые часто применяются в различных областях науки и повседневной жизни. Частное обычно обозначается символом "÷", а произведение – знаком умножения "×". Обе операции имеют свои особенности и применяются в разных контекстах.
Частное в математике представляет собой результат деления одного числа на другое. Оно показывает, сколько раз второе число содержится в первом. Например, если мы разделим число 10 на 2, результатом будет 5, так как 2 содержится в 10 пять раз. Частное может быть целым числом или десятичной дробью, в зависимости от чисел, которые делят и делятся.
Произведение, в свою очередь, представляет собой результат умножения двух или более чисел. Оно показывает, сколько раз мы берем одно число и складываем его с самим собой. Например, если мы умножим число 3 на 4, результатом будет 12, так как мы берем число 3 и складываем его с самим собой четыре раза. Произведение также может быть целым числом или десятичной дробью, в зависимости от чисел, которые умножаются.
Что такое частное в математике?

Частное обозначается символом "/" или двоеточием ":". Если числа A и B делятся одно на другое, то частное обозначается как "A / B" или "A : B".
Частное имеет такие свойства:
- Частное отрицательных чисел - это отрицательное число, если делимое и делитель имеют разные знаки, или положительное число, если знаки совпадают.
- Если делимое равно нулю, то частное всегда равно нулю.
- Если делитель равен нулю, то частное неопределено или бесконечно.
- Частное не зависит от порядка действий, то есть результат деления будет одинаковым независимо от того, какое число будет делимым, а какое - делителем.
Частное в математике широко используется для решения различных задач, а также для определения других математических операций, таких как производная и интеграл.
Основные свойства частного в математике

- Ассоциативность: порядок совершения операций в частном не влияет на результат. То есть для любых трех чисел a, b и c выполнено равенство (a / b) / c = a / (b / c).
- Коммутативность: порядок чисел не влияет на результат деления. То есть для любых двух чисел a и b выполнено равенство a / b = b / a.
- Идентичность: всегда существует число, на которое можно делить любое другое число, сохраняя его неизменным. Это число называется единицей и обозначается е. То есть для любого числа a выполнено равенство a / e = a.
- Делимость на 0: деление на ноль не определено в математике. То есть для любого числа a не существует числа b, такого что a / 0 = b.
- Обратимость: каждое число, кроме нуля, имеет обратное по отношению к частному. Обратное число обозначается как 1/a, и при умножении его на исходное число a получается единица: a * (1/a) = 1.
- Аддитивность: результат деления двух сумм равен отношению суммы каждого числа к делителю. То есть для любых четырех чисел a, b, c и d выполнено равенство (a + b) / (c + d) = (a/c + b/d).
Знание данных свойств помогает в решении различных задач и упрощает математические вычисления.
Что такое произведение в математике?
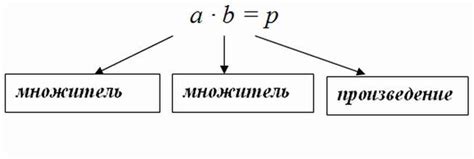
Произведение обозначается знаком умножения (×) или точкой (·). Например, выражение 2 × 3 или 2 · 3 обозначает произведение чисел 2 и 3.
При умножении чисел результат называется произведением. Например, произведение чисел 2 и 3 равно 6.
Произведение обладает рядом особенностей:
- Произведение двух чисел всегда больше или равно каждому из сомножителей. Например, произведение 2 и 3 больше 2 и больше 3.
- Порядок сомножителей не влияет на результат произведения. Например, произведение 2 и 3 равно произведению 3 и 2.
- Произведение числа на 1 равно этому числу. Например, произведение числа 5 на 1 равно 5.
- Произведение числа на 0 равно 0. Например, произведение числа 4 на 0 равно 0.
Произведение имеет множество приложений в реальном мире и используется в различных областях, таких как физика, экономика, статистика и другие.
Основные свойства произведения в математике

Вот основные свойства произведения в математике:
| Свойство | Описание |
|---|---|
| Коммутативность | Порядок множителей не влияет на итоговое произведение: a × b = b × a. |
| Ассоциативность | Порядок выполнения произведений не влияет на итоговое произведение: (a × b) × c = a × (b × c). |
| Дистрибутивность | Произведение можно распределить по сумме или разности: a × (b + c) = a × b + a × c. |
| Единица | Умножение на единицу не изменяет значение числа: a × 1 = a. |
| Ноль | Умножение на ноль всегда дает ноль: a × 0 = 0. |
Эти свойства произведения являются фундаментальными и широко применяются во многих областях математики и ее приложениях.
Что определяет частное двух чисел?
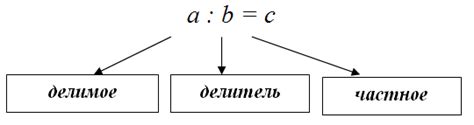
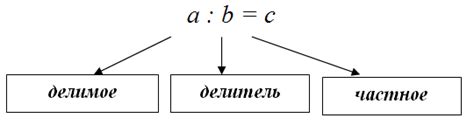
Частное двух чисел определяет результат деления одного числа на другое. Математически обозначается символом "/" или горизонтальной чертой. Первое число, которое делят, называется делимым, а второе число, на которое делят, называется делителем.
Чтобы найти частное, необходимо разделить делимое на делитель. Частное может быть как целым числом, так и десятичной дробью. В некоторых случаях, когда деление невозможно (делитель равен нулю), частное считается бесконечностью или неопределенным.
Частное является основным понятием в арифметике и используется для решения различных задач. Оно позволяет определить отношение между двумя числами и вычислять доли, коэффициенты и многое другое.
Частное также имеет определенные особенности. Например, если делитель меньше делимого, частное будет меньше единицы. Если же делитель больше делимого, частное будет больше единицы. Кроме того, частное может быть округлено до определенного количества знаков после запятой в зависимости от требуемой точности.
Разбиение числа на делимое и делитель позволяет более точно определить взаимосвязь между этими числами и использовать частное в различных математических операциях.
Как вычислить частное двух чисел?
Вычисление частного может быть с помощью ручного деления или использования калькулятора. Ручное деление требует некоторых навыков и знания деления в столбик, а использование калькулятора делает процесс более простым и быстрым. В обоих случаях результатом деления будет частное – целое или десятичное число.
Чтобы вычислить частное двух чисел ручным методом, необходимо выполнить следующие шаги:
- Записать делимое и делитель вертикально, выровняв их по правому краю.
- Поставить подчеркивание под делимое.
- Разделить первую цифру делимого на делитель. Результат будет первой цифрой частного, которую записываем над подчеркиванием.
- Умножаем делитель на полученную цифру и записываем результат под строчкой.
- Вычитаем полученное произведение из делимого и записываем результат подчеркиванием справа от предыдущего разряда.
- Продолжаем процесс деления с новым делимым, состоящим из записанной разницы и следующей цифры доходя до конца.
- Если остаток равен нулю или достигает значения указанной точности, процесс деления заканчивается.
Таким образом, вычисление частного двух чисел является стандартной операцией и может быть выполнено ручным или калькуляторным методом.
Что определяет произведение двух чисел?

Произведение двух чисел обозначается символом "×" или "*", и записывается в виде "a × b" или "a * b", где "a" и "b" - это множители. Результат умножения называется произведением и обозначается символом "⋅" или "*", например, "a ⋅ b" или "a * b".
Произведение двух чисел определяется как сумма их повторяющихся слагаемых. Например, произведение чисел 3 и 4 равно 12, потому что 3 + 3 + 3 + 3 = 12.
Произведение двух чисел также может быть интерпретировано как площадь прямоугольника, у которого одна сторона равна первому числу, а другая сторона равна второму числу. Например, если первое число равно 3, а второе число равно 4, то произведение будет равно площади прямоугольника со сторонами 3 и 4, то есть 12 квадратных единиц.
Кроме того, произведение двух чисел имеет несколько особенностей. Если один или оба множителя равны нулю, то их произведение также будет равно нулю. Если же одним из множителей является единица, то произведение будет равно другому множителю.
В общем случае произведение двух чисел может быть положительным, отрицательным или нулевым в зависимости от значений множителей.
Важно помнить:
- Произведение двух чисел - результат умножения множителей.
- Произведение обозначается символами "×" или "*", результат - символами "⋅" или "*".
- Произведение двух чисел может быть интерпретировано как сумма повторяющихся слагаемых или как площадь прямоугольника.
- Произведение двух чисел имеет особенности в зависимости от значений множителей.
Как вычислить произведение двух чисел?

Для вычисления произведения двух чисел необходимо выполнить следующие шаги:
- Возьмите первое число и умножьте его на второе число.
- Результат умножения будет являться произведением двух чисел.
Например, если у вас есть числа 5 и 3, то произведение этих чисел будет равно 15. Выполнив умножение 5 на 3, получим результат 15.
Важно помнить, что произведение двух чисел будет зависеть от операции умножения. В случае умножения двух положительных чисел, произведение также будет положительным числом. Если одно из чисел отрицательное, то произведение будет отрицательным числом. Если оба числа отрицательные, то произведение снова станет положительным числом.
Таким образом, вычисление произведения двух чисел является простой и основной операцией в математике, часто используемой как в повседневной жизни, так и в более сложных математических задачах.
Отличие частного от произведения в математике

Частное - это результат деления одного числа на другое. Оно выражает, сколько раз одно число содержится в другом. Например, если мы разделим число 10 на число 2, то получим частное 5. Это означает, что число 2 содержится в числе 10 пять раз.
Произведение, с другой стороны, является результатом умножения двух чисел. Оно показывает, сколько раз число увеличивается само на себя. Например, произведение чисел 5 и 2 равно 10, так как число 5 увеличивается само на себя два раза.
Таким образом, основным отличием между частным и произведением является то, что частное показывает, сколько раз одно число содержится в другом, а произведение показывает, сколько раз число увеличивается само на себя.
| Частное | Произведение |
|---|---|
| Результат деления | Результат умножения |
| Выражает, сколько раз одно число содержится в другом | Выражает, сколько раз число увеличивается само на себя |
Применение частного и произведения в математике

- Применение частного:
- В дробях: частное двух чисел представляет собой результат деления одного числа на другое. Дроби являются важным инструментом для точного представления и работы с нецелыми числами.
- В предметах со сравнительными характеристиками: частное двух величин может указывать на отношение между ними. Например, в физике частное скорости и времени дает расстояние, пройденное телом.
- Применение произведения:
- В умножении: произведение двух чисел представляет собой результат умножения одного числа на другое. Умножение является одной из основных операций в арифметике и используется во множестве математических концепций и формул.
- В математическом моделировании и статистике: произведение может описывать зависимости между различными переменными. Например, в модели Лотки-Вольтерры произведение численности популяции хищников и жертв используется для описания их взаимодействия.
Важно отметить, что применение частного и произведения в математике не ограничивается вышеуказанными примерами. Эти операции являются фундаментальными в математическом анализе и алгебре, и их использование может быть очень разнообразным в зависимости от конкретной задачи или области исследования.



