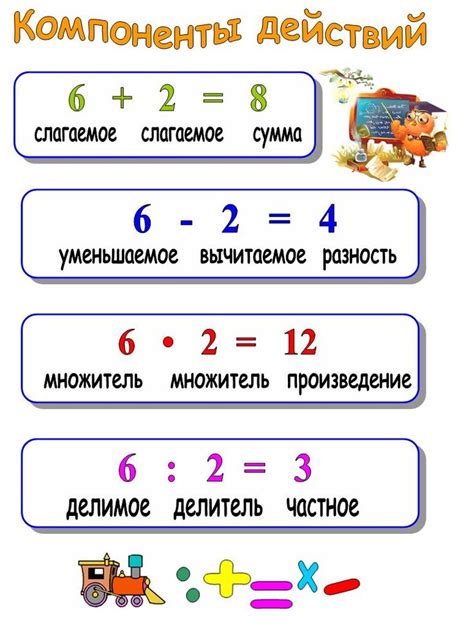
Частное и произведение – это основные математические понятия, которые изучаются уже во втором классе. Они являются основой для дальнейшего изучения арифметики и алгебры. Правила работы с частным и произведением представляют собой основополагающие навыки, которые позволяют ученикам решать разнообразные математические задачи.
Частное – это результат деления одного числа на другое. Для его нахождения необходимо поделить делимое на делитель. Важно помнить, что частное может быть как целым числом, так и дробным. В случае, если деление не возможно (например, при делении на ноль), частное считается неопределенным.
Произведение – это результат умножения двух или более чисел. Оно показывает, сколько раз нужно взять одно и то же число, чтобы получить заданное количество разных чисел столько же раз, сколько их в данном произведении. Например, произведение 3х4 равно 12, что означает, что нужно взять число 3 четыре раза, чтобы получить число 12.
Определение частного и произведения

В математике частным называется результат деления одного числа на другое. Частное не всегда будет являться целым числом, оно может быть и дробным. Чтобы найти частное, нужно разделить делимое на делитель. Для символического обозначения частного используется знак деления \(\div\) или обычная черта.
Произведением двух чисел называется результат умножения этих чисел. Произведение всегда будет являться числом, оно может быть как целым, так и дробным. Для символического обозначения произведения используется знак умножения \(\times\) или обычная точка.
Например, если у нас есть задача найти частное 15 и 3, то мы делим 15 на 3 и получаем результат 5. Символическое обозначение будет \(15 \div 3 = 5\). Если нам нужно найти произведение 5 и 4, то мы перемножаем эти числа и получаем результат 20. Символическое обозначение будет \(5 \times 4 = 20\).
| Делимое | Делитель | Частное |
|---|---|---|
| 15 | 3 | 5 |
| Множитель 1 | Множитель 2 | Произведение |
|---|---|---|
| 5 | 4 | 20 |
Правила деления чисел
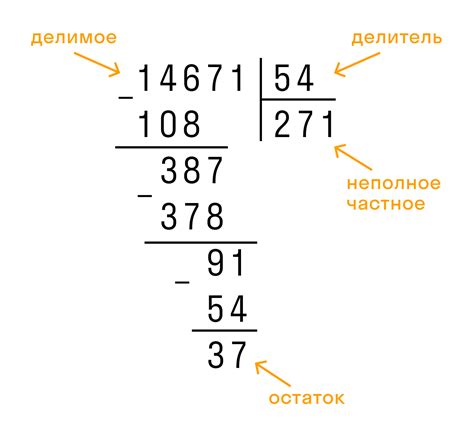
Например, если мы хотим разделить 12 на 3, то результат будет 4, потому что 4 умножить на 3 равно 12.
12 : 3 = 4
Правило 2: Если делитель равен 1, то частное будет равно делимому.
Например, если мы хотим разделить 15 на 1, то результат будет 15, потому что 15 умножить на 1 равно 15.
15 : 1 = 15
Правило 3: Если делитель равен нулю, то деление невозможно.
Например, если мы хотим разделить 8 на 0, то деление невозможно.
В результате получим неопределенное значение.
8 : 0 = Невозможно
Правила умножения чисел

Умножение чисел это операция, при которой два множителя объединяются в одну группу, чтобы найти их произведение или результат умножения.
Важные правила умножения чисел:
1. Коммутативность: порядок перемножаемых чисел не важен. Например, 5 * 3 это то же самое, что и 3 * 5.
2. Ассоциативность: порядок, в котором вы умножаете несколько чисел, не важен. Например, (2 * 3) * 4 это то же самое, что и 2 * (3 * 4).
3. Распределительный закон: умножение числа на сумму двух или более чисел дает то же самое, что и умножение каждого слагаемого на это число и затем сложение результатов. Например, 2 * (4 + 3) это то же самое, что и (2 * 4) + (2 * 3).
Примеры умножения чисел:
1. 3 * 2 = 6
2. 4 * 5 = 20
3. 7 * 0 = 0
4. 9 * 1 = 9
5. 6 * 6 = 36
Помните эти правила и используйте их для решения задач на умножение. Удачи!
Частное и произведение двузначных чисел

Частное двузначных чисел получается путем деления одного двузначного числа на другое. Чтобы разделить двузначное число на другое двузначное число, нужно выполнить следующие действия:
- Запишите делимое число и делитель в столбик, так чтобы единицы и десятки были выровнены.
- Начните деление, смотря на количество десятков в делимом числе, чтобы подобрать первую цифру частного.
- Если десятки делимого числа меньше делителя, перенесите следующую цифру из разряда единиц делимого числа и добавьте ее к десяткам. Это позволит провести деление и выбрать следующую цифру частного.
- Запишите полученную цифру частного в результирующий столбик.
- Умножьте полученную цифру частного на делитель и вычтите это произведение из делимого числа.
- Получите новое делимое число и повторите шаги 2-5, пока не останется число меньше делителя.
Произведение двузначных чисел можно найти путем умножения одного двузначного числа на другое. Для этого нужно выполнить следующие действия:
- Запишите множимое число и множитель в столбик, так чтобы единицы и десятки были выровнены.
- Умножьте разряд единиц множимого числа на разряд единиц множителя и запишите результат в столбик.
- Умножьте разряд десятков множимого числа на разряд десятков множителя и запишите результат в столбик, сдвигая его влево на разряд.
- Умножьте разряд единиц множимого числа на разряд десятков множителя и запишите результат в столбик, сдвигая его влево на разряд.
- Умножьте разряд десятков множимого числа на разряд единиц множителя и запишите результат в столбик, сдвигая его влево на разряд.
- Сложите все полученные результаты, чтобы получить итоговое произведение двух двузначных чисел.
Зная правила частного и произведения двузначных чисел, вы сможете легко решать задачи и выполнять вычисления на уроках математики.
Частное и произведение трехзначных чисел
Для вычисления частного и произведения трехзначных чисел необходимо следовать определенным правилам. Чтобы получить правильный результат, вы должны использовать правильную последовательность действий.
Возьмем для примера два трехзначных числа: 234 и 567.
Чтобы найти частное этих чисел, вам нужно разделить первое число на второе:
| Делимое | Делитель | Частное |
|---|---|---|
| 234 | 567 | 0.412655 |
Чтобы найти произведение этих чисел, нужно умножить их друг на друга:
| Множимое | Множитель | Произведение |
|---|---|---|
| 234 | 567 | 132678 |
Надеюсь, эти примеры и правила помогут вам лучше понять, как находить частное и произведение трехзначных чисел. Практикуйтесь и вы сможете выполнять эти вычисления с легкостью!
Приложение: примеры вычисления частного и произведения

Давайте рассмотрим несколько примеров, чтобы лучше понять, как вычислять частное и произведение двух чисел.
Пример 1:
Даны два числа: 10 и 5.
Чтобы вычислить их частное, нужно разделить первое число на второе: 10 / 5 = 2.
Таким образом, частное чисел 10 и 5 равно 2.
Пример 2:
Даны два числа: 4 и 2.
Для вычисления произведения этих чисел, нужно умножить их: 4 х 2 = 8.
Полученное значение 8 является произведением чисел 4 и 2.
Пример 3:
Давайте рассмотрим пример с отрицательными числами: -6 и 3.
Чтобы вычислить их частное, нужно разделить -6 на 3: -6 / 3 = -2.
Таким образом, частное чисел -6 и 3 равно -2.
А для вычисления произведения отрицательных чисел, нужно умножить их: -6 х 3 = -18.
Значит, произведение чисел -6 и 3 равно -18.
Надеюсь, эти примеры помогли вам лучше понять, как вычислять частное и произведение чисел. Не забывайте применять эти правила в своих заданиях и упражнениях.
Задания для самостоятельной работы

Для закрепления темы "Частное и произведение" 2 класса, Вы можете выполнить следующие задания самостоятельно:
| Задание | Пример |
|---|---|
| Вычислить частное | 16 ÷ 4 = 4 |
| Вычислить произведение | 5 * 3 = 15 |
| Найти все делители числа 24 | Делители числа 24: 1, 2, 3, 4, 6, 8, 12, 24 |
| Найти частное от деления числа 45 на 9 | 45 ÷ 9 = 5 |
| Найти произведение чисел 7 и 6 | 7 * 6 = 42 |
Подумайте над каждым заданием, выполните несколько примеров, а затем проверьте себя. Удачи!
- Частное двух чисел можно найти, разделив одно число на другое.
- При делении чисел нацело, результат будет целым числом.
- При делении чисел с остатком, результат будет десятичной дробью.
- В произведении двух чисел нужно перемножить сомножители.
- Умножение коммутативно, то есть порядок сомножителей не имеет значения.
- Умножение числа на 0 всегда даёт 0.



