Призма - это геометрическое тело, которое имеет два многоугольника, называемых основаниями, и прямоугольники, называемые боковыми гранями, соединяющими эти основания. Но что такое боковая поверхность и полная поверхность призмы?
Боковая поверхность призмы - это сумма площадей всех ее боковых граней. Боковые грани призмы представляют собой прямоугольники, поэтому для вычисления площади боковой поверхности призмы нужно умножить периметр основания на высоту призмы. Таким образом, боковая поверхность призмы является показателем ее поверхностной площади, и может быть использована для нахождения объема призмы вместе с площадью основания.
Полная поверхность призмы - это сумма площадей всех ее граней, включая основания и боковые грани. Для нахождения полной поверхности призмы нужно сложить площади ее оснований и площадь боковой поверхности. Таким образом, полная поверхность призмы дает нам полную картину ее внешнего вида и может быть использована для различных геометрических вычислений, включая нахождение площади поверхности и объема призмы.
Что такое боковая поверхность призмы?
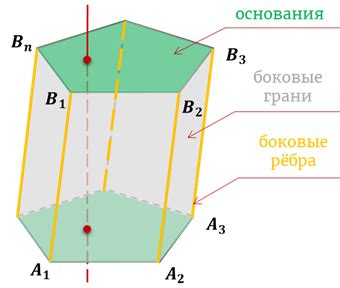
Боковая поверхность призмы может иметь различные формы в зависимости от формы призмы. Например, у треугольной призмы боковая поверхность будет состоять из трех прямоугольных треугольников, у прямоугольной призмы - из четырех прямоугольников, а у шестиугольной призмы - из шести правильных шестиугольников.
Боковая поверхность призмы имеет несколько особенностей. Во-первых, она заключает в себе объем призмы и помогает определить ее геометрические свойства, такие как ее высота, длина ребер и площадь полных поверхностей. Во-вторых, боковая поверхность призмы обладает рядом математических свойств, которые позволяют рассчитывать ее площадь или взаимосвязь с другими элементами призмы.
Определение и понятие

Полная поверхность призмы состоит из боковой поверхности и оснований. Основаниями призмы являются многоугольные фигуры, соединенные ребрами с боковыми гранями. Полная поверхность призмы включает все эти составляющие и является суммой их площадей.
Понятие боковой и полной поверхности призмы важно при изучении геометрии и связано с понятиями объема и площади фигур. Они используются для вычислений и практического применения призмы в различных сферах, например, при строительстве или расчете объема жидкости в сосуде.
Формула и методы вычисления

Для вычисления боковой поверхности прямой призмы можно использовать следующую формулу:
Боковая поверхность = периметр основания * высота призмы
Периметр основания призмы рассчитывается по формуле, соответствующей типу основания. Например, для прямоугольной призмы периметр рассчитывается по формуле:
Периметр = 2 * (длина + ширина)
Чтобы найти полную поверхность призмы, нужно сложить боковую поверхность и удвоенную площадь основания:
Полная поверхность = Боковая поверхность + 2 * Площадь основания
Формулы для вычисления боковой поверхности и полной поверхности могут варьироваться в зависимости от формы и типа призмы. Важно иметь аккуратные и правильно измеренные значения основания, высоты и прочих параметров при использовании этих формул.
Свойства и особенности

Боковая поверхность призмы представляет собой обычно прямоугольник или параллелограмм, состоящий из одинаковых боковых граней. Эти грани соединяют вершины оснований призмы.
Полная поверхность призмы включает все грани, включая основания и боковые грани. Она образует замкнутую фигуру, охватывающую всю призму.
Свойства боковой поверхности призмы:
- Боковые грани призмы параллельны и равны друг другу по размерам и форме;
- Угол между боковыми гранями призмы равен углу между основаниями;
- Боковые грани призмы перпендикулярны к основаниям.
Свойства полной поверхности призмы:
- Полная поверхность призмы состоит из нескольких граней, включая основания и боковые грани;
- Форма полной поверхности призмы зависит от формы оснований и количества боковых граней;
- Полная поверхность призмы представляет собой замкнутую фигуру, охватывающую всю призму.
Таким образом, боковая поверхность и полная поверхность призмы обладают определенными свойствами и формируют важные составляющие ее геометрической структуры.
Примеры и применение
Например, представим себе кирпич. Боковая поверхность кирпича имеет форму прямоугольника, а полная поверхность включает еще и верхнюю и нижнюю грани. Зная размеры кирпича, можно легко рассчитать его объем, а также площадь его боковой и полной поверхности.
Другой пример – параллелепипед. Боковая поверхность параллелепипеда состоит из четырех прямоугольников, в то время как полная поверхность включает еще и верхнюю и нижнюю грани. Полезность знания площади боковой поверхности и полной поверхности параллелепипеда особенно проявляется при рассмотрении задач по упаковке и хранению различных предметов.
Другим практическим примером является использование знания о боковой и полной поверхности призмы в архитектуре. Архитекторы рассчитывают площади боковых и полных поверхностей, чтобы определить необходимое количество материалов для строительства здания, а также для рассчета высот и объемов помещений.
Что такое полная поверхность призмы?
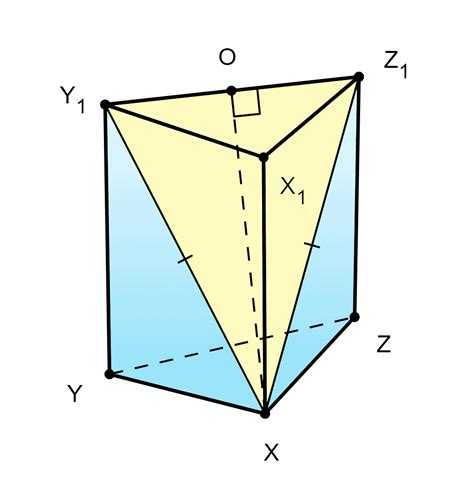
Боковая поверхность призмы - это прямоугольник, у которого одна сторона равна высоте призмы, а другая сторона - периметру основания призмы. Для расчета площади боковой поверхности призмы можно использовать формулу: Sб = П * h, где h - высота призмы, П - периметр основания.
Периметр основания призмы - это сумма длин всех сторон основания. Если основание призмы является прямоугольником, то периметр можно найти по формуле: П = 2 * (a + b), где a и b - длины сторон основания. Если основание призмы имеет форму другого многоугольника, периметр можно найти, сложив длины всех его сторон.
Площадь основания призмы - это произведение длин двух его сторон (для прямоугольного основания) или площади многоугольника (для других форм основания).
Таким образом, полная поверхность призмы можно расчитать, суммируя площади оснований и боковой поверхности призмы. Формула для расчета полной поверхности: Sп = Sб + 2 * Sосн, где Sп - полная поверхность призмы, Sб - площадь боковой поверхности, Sосн - площадь каждого основания призмы.
| Тип основания | Формула площади основания | Формула площади боковой поверхности | Формула полной поверхности |
|---|---|---|---|
| Прямоугольное | Sосн = a * b | Sб = П * h | Sп = Sб + 2 * Sосн |
| Квадратное | Sосн = a * a | Sб = П * h | Sп = Sб + 2 * Sосн |
| Треугольное | Sосн = (a * h) / 2 | Sб = П * h | Sп = Sб + 2 * Sосн |
Определение и понятие

Полная поверхность призмы - это сумма площадей всех ее граней. В общем случае, полная поверхность призмы представляет собой основания призмы и ее боковую поверхность. Площадь полной поверхности призмы включает в себя площади всех граней призмы, включая основания и боковую поверхность. Формула для нахождения площади полной поверхности призмы зависит от формы и размеров оснований, а также от формы и размеров боковых граней.
Наличие боковых поверхностей и полной поверхности призмы является одним из ключевых понятий в геометрии, которое часто применяется в решении задач по измерению и пространственным структурам. Понимание этих понятий позволяет определить объемы и площади призмы, а также проводить расчеты и анализировать их физические свойства и характеристики.



